Inscription / Connexion Nouveau Sujet
Cesàro en version continue
Bonjour à tous,
Pour ceux que ça intéresse, voici un petit exercice d'analyse :
Tout le monde connaît le théorème de Cesàro pour les suites :
Si une suite converge vers L alors la moyenne de cesàro :
converge aussi vers L.
Maintenant : Soit f une fonction continue pour laquelle la quantité f(x+1)-f(x) admet une limite lorsque x tend vers l'infini. Montrer que tend vers cette même limite.
J'ai trouvé une démonstration dont je ne suis pas sûr, je vous la soumettrai lorsque j'aurais vu un peu les différents raisonnements employés (encore faut-il qu'il en existe plusieurs).
Bonne résolution 
Salut Noflah
Après un peu de recherche, je suis convaincue qu'il faut un peu de topologie et je ne sais pas de quoi tu disposes... Alors pour commencer, voilà un nouvel exercice qui concentre la difficulté et qui entraine facilement le tien:
Soit
Pour ce faire j'utilise la compacité de [1,2]. Si tu ne sais pas, on peut toujours faire un peu d'acrobaties pour se ramener à des résultats plus élémentaires.
Bonjour Camélia,
En fait pour démontrer le résultat que je propose, j'ai utilisé le tien, mais sans réellement le démontrer (du genre "c'est logique").
Voici ma démonstration : (désolé les signes  ne sont pas sortis, j'ai utilisé
ne sont pas sortis, j'ai utilisé ![]() ce site pour écrire mon texte).
ce site pour écrire mon texte).
Un ami, qui a lui aussi eu cette intuition mais qui ne la trouvait pas assez rigoureuse est descendu plus bas : (deuxième image)
(non précisé sur l'image : x1 est tel que x0=E(x1) / la majortion de la dernière ligne permet de majorer chacun des terme par e/3 afin d'obtenir le tout plus petit que epsilon (pour tout epsilon) )
Je vais donc réfléchir à comment démontrer ton résultat  Merci pour ton intervention.
Merci pour ton intervention.
(PS : je connais la compacité, mais je ne sais pas si je connais toutes les propriétés que l'on peut y appliquer. Je sais que tout suite convergente de K converge dans K, Bolzano Weirschtrass, et peut être d'autre résultat qui ne me viennent pas là comme ça. Bon je vais essayer et si je bloque j'appelle au secours  )
)
Encore merci Camélia !
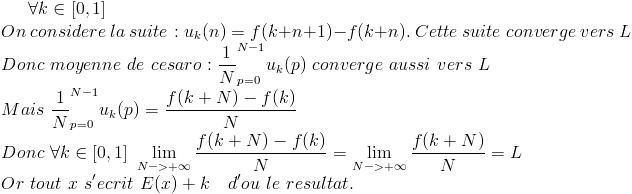
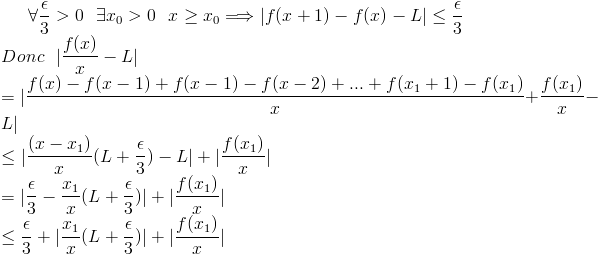
Oups, désolé on ne voit pas bien la limite entre les deux images, la première s'arrête à "d'ou le résultat". Mais j'avoue que quand j'ai écris ça je me doutais qu'il manquait un petit quelque chose pour justifier que de "pour tout x il y a une des suites qui marche" à "ça marche pour tout x", et je me suis dit qu'une petite définition de la continuité de f devait pouvoir faire le lien entre les différentes suites, qui diffèrent d'un petit "k" en fait. Non ?
Aussi, tu peux m'appeler Simon, comme tu as commencé à le faire dans d'autres post si je me souviens bien 
OK, Simon!
Comme ni toi ni ton ami n'utilisez la continuité, il y a forcément un os quelque part...
Pour l'instant je n'ai pas de contrexemple pour une fonction non continue...
Si ce genre de trucs t'amuse, voilà mon premier topic sur cette 
Bonjour 
C'est un exercice très classique de maniement de l'epsilon (souvent posé en colle). On peut d'ailleurs affaiblir l'hypothèse en supposant seulement f bornée sur tout segment (non nécessairement continue). La difficulté est de produire une rédaction qui ne soit pas trop lourde.
Je propose la mise en forme suivante dans le cas où la limite est finie :
Tout d'abord, on peut se ramener au cas où (en posant
).
Si , on a
où
.
étant continue et tendant vers
en
, on peut poser
et affirmer que
.
On a donc par encadrement :
.
D'autre part, et comme d'après Césaro,
, on obtient par composition puis encadrement :
.
Finalement, .
@Camélia :
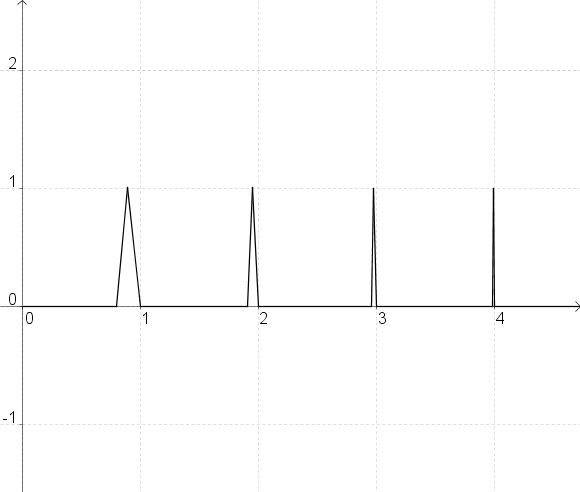
Je pense que ton résultat de 14:10 est faux : on peut construire un contrexemple avec des pics de plus en plus fins, situés à intervalles presque réguliers, l'abscisse des pics se rapprochant des entiers (je vais essayer de faire un dessin).
En revanche si on suppose l'uniforme continuité, je crois que ton truc marche.
Bonjour Onoff,
Merci pour ta contribution à l'exercice, en effet c'est un classique de kholle, je le tire moi même d'un recueil d'exercice de kholle classique ! (comme les quelques derniers exercices que j'ai posté).
Ton contre exemple annule-t-il ce résultat ? :
Citation :
Soit g:I -> R une fonction continue. On suppose que pour tout a de [1;2] la suite g(a+n) tend vers l. Alors ..
Si ce résultat tombe à l'eau, ma démonstration également ? (post du 23-07-10 à 14:20, première image) ?
Qu'en est-il de la deuxième démonstration ? (deuxième image) Est-elle fausse ?
Merci à vous deux pour votre aide

En relisant mieux la méthode d'Onoff, je viens de m'apercevoir que la méthode employé dans la deuxième image est très similaire, ce qui répond à ma question ci dessus.
Merci Camélia et Onoff 
et comme d'après Césaro
Je rends à Cesàro, ce qui est à Cesàro : l'orthographe de son nom.

Bonjour Onoff,
A titre d'entrainement, j'essaie, après l'avoir comprise, de voir si je suis capable de reproduire ta méthode.
Un passage du raisonnement m'échappe cependant :
A0 est le sup de epsilon, pas de f, donc on aurait,
Comment en arriver à la ligne précédente ?
Je te remercie d'avance 
Mais oui, Noflah, tu as raison, je me suis emmêlé dans mes notations. Il ne s'agit pas de A0 mais du sup de |f| sur [0;1].