Inscription / Connexion Nouveau Sujet
Challenge n°80



Bonjour,
ca faisait longtemps que je nous vous avais pas proposé des énigmes plus piquantes que celles côtées à une étoile... Voici donc une énigme de géométrie à quatre étoiles soigneusement analysée et approuvée par le conseil des sages :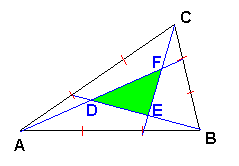
Soit un triangle quelconque ABC d'aire S.
Chacun de ses cotés est divisé en 3 parts égales.
On forme alors un nouveau triangle DEF par la construction montrée sur le dessin.
L'aire du triangle DEF est notée "s".
Quelle est la valeur exacte du rapport s/S ?
Démonstration recquise.
Bonne chance à tous,
clôture lundi soir.
 Les notations sont celles de mon dessin!! Pardon c'est trop tard pour je refasse tout !!
Les notations sont celles de mon dessin!! Pardon c'est trop tard pour je refasse tout !!
Je remarque de A(CEA) est égale 1/3 de S (même hauteur et base égale au tiers).
Ona donc s= S-(1/3 S+1/3 S+ 1/3 S)+ 3 A(DEA)
En supposant que les trois triangles de "type" DEA de sommet B et C ont la même aire.
On remarque que DEA et DFG sont semblables de rapport 1/2. La hauteur de DEA est donc égale à 1/3 EF = 1/9 H (avec H hauteur de ABC issue de C)
A(DEA) = 1/2 *1/9*1/3 *H*AB= 1/27* S
Ma supposition concernant les trois triangles de type DEA est donc exacte.
s= S-(1/3 S+1/3 S+ 1/3 S)+ 3 *1/27*S = 1/9*S
s/S= 1/9





Démonstration par la géométrie analytique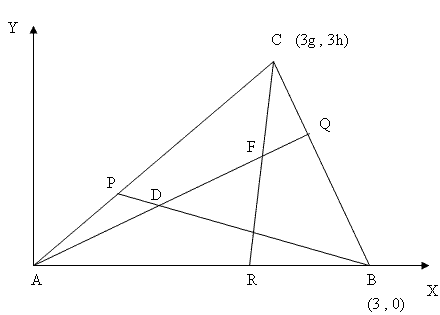
Je place A à l'origine O des axes. Je peux poser B(3,0) et C(3g,3h).
L' aire du triangle ABC est alors .
P au tiers de [AC] à partir de A : P(g,h)
R au deux tiers de [AB] à A : R(2,0)
Calcul de la coordonnée de Q au deux tiers de [BC] à partir de B =
+
.
=
+
.(
-
) =
.
+
.
On en déduit que Q(1+2g,2h)
Equation de DF (ou encore OQ)
Equation de DE
Son coefficient de direction vaut
Son équation est donc + p
Comme (3,0) est un pt de cette droite : p =
Donc DE a pour équation
Pour EF, je trouve
Coordonnée de D(xD , yD)
L'abscisse est solution de =
.
Je trouve
L' ordonnée vaut alors .
(2g+1) =
D( ,
)
On trouve de la même manière E( ,
) et F(
,
)
L' aire s du triangle DEF s'obtient en divisant par deux la valeur absolue du déterminant suivant
| xD yD 1 |
| xE yE 1 | (faudrait que je me mette à essayer de faire des tableaux)
| xF yF 1 |
Ce déterminant vaut (2g+1).(
-
) -
.(
-
) +
(2g+1).(
-
)
=...... = .
Donc s = =
.
On a donc =
.
=
=
 la réponse est 1/7
la réponse est 1/7
on exprime les points D E F comme les barycentres en fonction de A B C
on commence par exprimer les points G H I au 1er tiers de AC BA et CD, puis sachant que les points D E et F sont sur le croisement de 2 segments, 3 points alignés nous donnant 2 vecteurs colinéraires, on obtient un système d'équation duquel on tire :
7F = 1A + 2B + 4C et pareil pour les autres en tournant
On doit pouvoir conclure en beauté mais mes souvenirs flanches, j ai donc posé A(0,0) B(x,0) C(x,y)
trouvé les coordonnées de D E F et fait le produit scalaire me donnant la surface s=zx/7
sachant que S=zx, s/S=1/7




 je n'arrive malheuresement pas à joindre ma figure, donc la lecture sera moins aisée. je vais tout de même essayer d'etre clair.
je n'arrive malheuresement pas à joindre ma figure, donc la lecture sera moins aisée. je vais tout de même essayer d'etre clair.
je me place dans le repère de centre le point O tel que AO = 2AB/3, d' axes (OB) et (OC) et d'unité 0B.
on a alors:
A(-2;0),
B(1;0)
C(O,h) , h variant.
Soit G le point d'intersection de (AF) et (BC)
Soit H le point d'intersection de (BD) et (AC)
ainsi, les coordonnées de G et H sont:
H(-4/3;h/3)
G(1/3;2h/3)
la droite (AG) a pour équation y = (2h/7)x + 4h/7
la droite (BH) a pour équation y = (-h/7)x + h/7
on en déduit les coordonnées de D(-1;2h/7)
( remarque intéressante, lorsque h varie, le point D reste sur une droite parallèle à l'axe des ordonnées)
Les points E et F appartiennent à (OC), et leurs coordonnées sont
E(0;h/7)
F(0;4h/7)
la longeur EF est donc EF = 3h/7
On change maintenant de repère pour calculer les aires.On fait tourner l'axe (OC) des ordonnées de sorte qu'il se retrouve perpendiculaire à l'axe (OB).
Dans ce nouveau repère C(h cosâ;hsinâ) et D(cosâ;2hsinâ/7)
(l'angle â dépend de la position de C, mais c'est sans importance pour la suite)
remarque: dans ce nouveau repère, la distance EF ne change pas.
on va calculer les aires dans ce nouveaux repère qui lui est orthonormé.
s = xD * EF /2
= 3h*cosâ/14
S = h*cosâ*3/2
Ainsi, s/S = (3h*cosâ/14)/(h*cosâ*3/2)
ce qui après simplification donne 1/7
Y'a plus simple, non? 
 "Petit" problème très sympa et joli résultat! Merci puisea.
"Petit" problème très sympa et joli résultat! Merci puisea.
Bon, j'ai voulu le tout-géométrique mais j'ai échoué sur un point qui fait quand même tâche. Tant pis!
Préliminaire:
I,J,K,L,M,N sont les divisions en 3 parties des côtés.
X,Y,Z les milieux respectifs de [AB],[BC] et [AC].
Voici la partie honteuse.
* Montrons que D (IZ):
Je me place dans un repère (A;B;C)
On a les coordonnées suivantes:
A(0;0), B(1;0), C(0;1), I(1/3;0), N(0;1/3), L(1/3;2/3) et Z(0;1/2)
(AL) a pour équation y = 2x et (BN) a pour équation x + 3y = 1
On en déduit les coordonnées de D, intersection de ces deux droites: D(1/7;2/7)
D'autre part, (ZI) a pour équation 3x + 2y = 1. On vérifie alors que D (IZ)[/b] ( =beurk=! )
* De même, E (KX)[/b] et F
(MY)[/b].
_________________________________________________________________________________________________
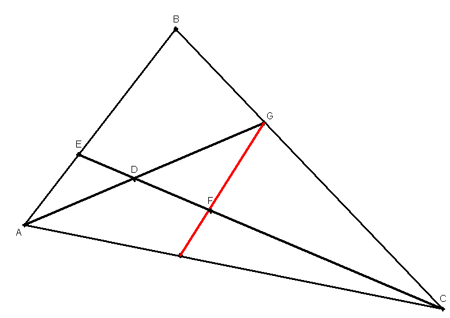
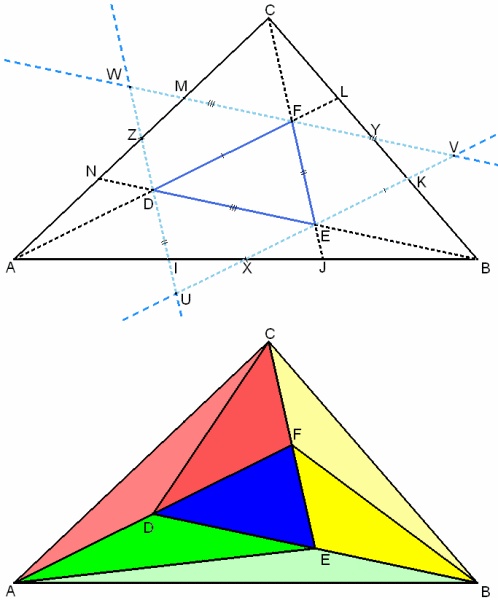
On construit les droites (IZ), (KX) et (YM) qui se coupent aux points U,V et W (voir figure ci-dessous).
Dans le triangle ACJ, I et Z sont les milieux respectifs de [AJ] et [AC] donc,
d'après le théorème de la droite des milieux, (IZ) est parallèle à (CJ).
De même, (KX)//(AL) et (MY)//(BN).
D'après le préliminaire (les points I,D,Z étant alignés), (IZ)//(CJ) s'écrit aussi (ID)//(FJ).
Ensuite, dans le triangle AFJ, d'après la seconde propriété de la droite des milieux,
comme I est le milieu de [AJ] et que (ID)//(FJ), on sait que (ID) coupe [AF] en son milieu.
Ainsi D est le milieu de [AF].
On prouve de façon analogue que : E est le milieu de [BD] et F est le milieu de [CE].
Enfin, on peut passer à la partie intéressante : Le découpage (seconde figure).
* Les triangles ADE et DEF possèdent :
- la même hauteur issue du sommet commun E;
- des bases dans le prolongement (droites confondues);
- des bases de même longueur associée puisque AD = DF (D est le milieu de [AF]),
donc ont la même aire !
* De même, les triangles verts ADE et ABE ont même aire, car la même hauteur issue de A et des bases égales ( DE = EB ).
* De façon identique, on montre que les triangles rouges et les triangles jaunes ont même aire que le triangle DEF.
Finalement, le triangle ABC a été découpé en triangles de même aire. Le triangle DEF étant une de ces 7 parties,
son aire représente exactement ( =
) de l'aire du triangle ABC.
 Je nomme A' est l'intersection de AF avec BC, B' l'intersection de BD et AC et C' l'intersection de CE avec AB. Je pose encore ||AB||=c, ||BC||=a et ||CA||=b.
Je nomme A' est l'intersection de AF avec BC, B' l'intersection de BD et AC et C' l'intersection de CE avec AB. Je pose encore ||AB||=c, ||BC||=a et ||CA||=b.
Si represente l'aire d'un triangle on a
En sommant l'aire de ces trois triangles on se rend compte que . Je me lance donc dans le calcul de ces trois petits triangles...
On voit facilement que
A' barycentre de (B,1) (C,2)
B' barycentre de (A,2) (C,1)
C' barycentre de (A,1) (B,2)
D est sur la droite AA' et aussi sur la droite BB' donc D barycentre de (A,4), (B,1), (C,2).
E est sur CC' et BB' donc E barycentre de (A,2),(B,4),(C,1).
F sur CC' et AA' donc F barycentre de (A,1),(B,2),(C,4).
Comme D est le barycentre de (A,4), (B,1), (C,2), l'aire des triangles seront proportionelles à 4, 1 et 2 et on a
Le même raisonnement permet de trouver que
Finalement on a et donc
Il y a probablement une résolution plus simple, mais je n'ai pas la tête très au clair ce matin...
Isis




 Hello donc bonjour tout le monde motivé pour faire toutes les enigmes alors j'y go:
Hello donc bonjour tout le monde motivé pour faire toutes les enigmes alors j'y go:
Voici mon raisonnement (image explicative a la fin):
Prenons le repère (;
;
)
B(1;0) C(0;1) I(;0) K(
;
)
AK:
CI:
et
Donc
Je peux par cela dire que l'aire du triangle DEF est égal à:
Aire totale du triangle - ((somme des aires des triangles A1+A2+A3) - (somme des aires des triangles a1+a2+a3))
Ce qui nous donnes:
Donc je viens de démontrer que l'aire s du triangle DEF vaut de l'aire S du triangle ABC
Voir figure annexe
++ EmGiPy ++




on fait des parallèles de DE, DF, EF passant par les sommets A, B, C, D, E, F,
si on considère l'aire du triangle EDF comme 1, on a
(aire) ADB= 1/2 (aire)ADBC'=2 car ADBC' est composé de 4 EDF
de meme AFC=CBC'=2
on a
ABC=DEF+CBC'+ABB'+ACF=7
donc DEF=1/7 ABC




 Bon allez qui ne tente rien n'a rien comme on dit ...
Bon allez qui ne tente rien n'a rien comme on dit ...
Beaucoup de calculs donc grande probabilité d'erreurs mais bon ...
On note les coordonnées des Points A,B et C :
On en deduit la position des 3 point D,E et F :
On parametre les 3 droites qui vont former les les cotés du nouveau triangle:
1:
2:
3:
Grace a ces 3 equations parametriques on en deduit les coordonnées des trois points G,H et I comme intersections des droites 2 a 2:
Maintenant qu'on connait toutes les coordonnées on calcule l'aire grace au produit vectoriel :
On trouve
Et
D'ou finalement
Et voila j'espere ne pas avoir fais d'erreur de raisonnement ni d'erreur de recopie de ma demo. Il y avais certainement plus simple car cette methode est assez lourde en calculs ... mais bon le resultat a l'air correct ...
 Bonjour la solution est 1/3.
Bonjour la solution est 1/3.
Voila, en esperant de ne pas m'être trompé.
 J'ai dans un premier temps pour objectif de déterminer le rapport de l'aire du triangle rouge ABB2 par rapport à celle de ABC.
J'ai dans un premier temps pour objectif de déterminer le rapport de l'aire du triangle rouge ABB2 par rapport à celle de ABC.
A1 est barycentre de {(B,2),(C,1)}
A2 est sur la droite(AA1) donc barycentre de {(A,a),(A1,b)} donc de {(A,a),(B,2b),(C,b)}
C1 est barycentre de {(A,2),(B,1)}
A2 est sur la droite(CC1) donc barycentre de {(C1,c),(C,d)} donc de {(A,2c),(B,c),(C,d)}
Comme A,B et C sont non alignés, on a proportionnalité des coefficients du barycentre donc c=2d et donc A2 est barycentre de{(A,4),(B,2),(C,1)}
de la même façon, B2 est barycentre de{(A,1),(B,4),(C,2)} et C2 est barycentre de{(A,2),(B,1),(C,4)}
Donc en utilisant les propriétés du barycentre pour B2 :
soit un vecteur normé orthogonal à
La hauteur du triangle ABC issue de C vaut
La hauteur du triangle ABB2 issue de B2 vaut
De la même façon et
Avec les 3 triangles, on couvre (sans chevauchement) de ABC. L'aire du triangle A2B2C2 est donc égale à ce qui reste soit
J'avais une démonstration plus jolie basée sur les homothéties et Thalès mais que je n'arrivais pas à expliquer succinctement. Je vous laisse juste la figure que m'a permis de bien visualiser




 Bonjour,
Bonjour,
Réponse : 1/3
Soit hb la hauteur issue de B dans le triangle ABC
Soit hc la hauteur issue de C dans le triangle ABC
Soit ha la hauteur issue de A dans le triangle ABC
Soit ha’ la hauteur issue de A’ dans le triangle AA’C’
Soit hb’ la hauteur issue de B’ dans le triangle BB’A’
Soit hc’ la hauteur issue de C’ dans le triangle CC’B’
On a S(ABC) = (BC.ha)/2 = (AC.hb)/2 =(AB.hc)/2
et S ( CC’B’ ) = (CB’. hc’ )/2 avec CB’ = 1/3 CB
S ( BB’A’ ) = (BA’. hb’ )/2 avec BA’ = 1/3 BA
S ( AA’C’ ) = (AC’. ha’ )/2 avec AC’ = 1/3 AC
S(A’B’C’ )=
= S (ABC) – ( S(CC’B’ ) + S(BB’A’ ) + S(AA’C’ ) )
= S (ABC) – ( (1/3 CB . hc’ )/2 + (1/3 BA . hb’ )/2 + (1/3AC . ha’ )/2)
= S(ABC) – (1/6 CB . 2/3 ha + 1/6 BA . 2/3 hc + 1/6 AC . 2/3 hb)
= S(ABC) – ( 2/9 . ((CB . ha / 2) + (BA . hc/2) + (AC.hb/2)))
= S(ABC) – (2/3)S(ABC)
=(1/3)S(ABC)
Merci pour l'énigme,
Philoux
 bonjour ,
bonjour ,
pour moi le rapport mais je ne suis pas convaicu car ce n'est pas ce que donne un logiciel de mesure grapphique.
enfin le plus dur va etre de vous le demontrer car c'est tres tres long . si vous permettez je vais abreger.
la base est un repere orthonorme de centre A d'abcisse AB et d'ordonnees perpendiculaire en A a AB
G est lintersection de AF et CB
H de bd avec AC
I de CE abec AB
j'ai donne a chaque point des coordonnees et j'ai touve les equations des droites AG , BH , CI ; leurs intersections m'on donne les coordonnees des point D , E ,F puis celles des vecteurs
j'ai pu calculer la distance DF puis la distance de E au segment DF
et a partir de la calculer la surface du petit triangle.
maintenant passons aux details
coorbonnees: A(0,0) B(xb,0) C(xc,yc
I(2/3xb,0) G (2xc+xb)/3 ,2yc/3 H(xc/3, yc/3)
je passe sur les equations des droites les points d'intersection et je vais vous doner les vecteurs:
(2xc+xb)/7 , 2yc )
/7
(3xb-xc)/7 , -yc/7
( 2xb-3xc)/7 ,_3yc/7
DF2= ((2xc+xb)2+4yc2)/49
la distance de E au segment DF est la droite EH
EH = xbyc divise par la racine de
4yc2+(2xc+xb)2
l'aire s = EH *DF /2
= xbyc*(1/7)*(1/2)
l'aire S = xbyc*(1/2)
c'est lourd et long et encore je ne suis ps sur que cela soit juste quoique je l'ai verifie sur une solution nulmerique.
A ce soir pour le resultat
merci
Paulo
Merci à tous de votre participation, j'ai demandé la démonstration pour ne pas avoir des résultats au pif ou à la visualisation sur logiciel graphique...
La réponse était 1/7. Alors à la base ce n'était pas le même ennoncé, et il n'y avait même pas de figure, donc en prenant mes références, il y avait une manière plus simple et demandant moins de cacluls que ce que vous avez utilisé :
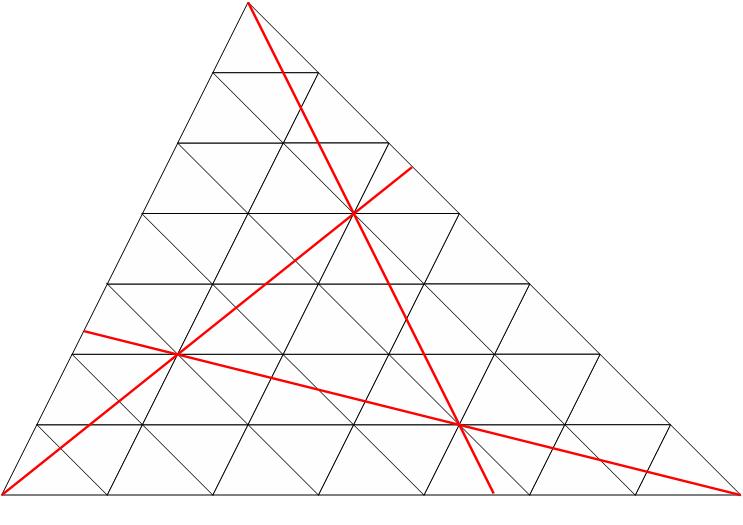
L'idée consiste à faire entrer le triangle ABC dans un triangle semblable au traingle d'aire s qui pourra donc être décomposé en un certain nombre de triangles identiques. Traçons d'abord le triangle quelconque ABC, puis les points A'1, B'1 et C'1 respectivement au tiers de CB, AC et BA, et enfin le triangle A'B'C' dont l'aire est s. On va maintenant faire passer par B une droite parallèle à B'C'. Pour cela on prolonge AC de CC1 = AC/2. On a alors : AC'1/AB = AC/AC1 = 2/3 et BC1 est parallèle B'C' (Thalès). En procédant de la même manière, on trace la parallèle à A'C' passant par C et la parallèle à A'B' passant par A.
On obtient le triangle MNP (tracé rouge), qu'on divise par un jeu de parallèle équidistantes. Le triangle MNP est ainsi décomposé en 16 triangles égaux à A'B'C'.
On compte : aire du traingle MNP = 16s. On place le point B2 et on compte : aire (BNCB2) = 6s, d'où la moitié : aire (BNC) = 3s (zone en vert). De même : aire (CPA) = 3s et aire(AMV) = 3s (zones en vert). Ainsi aire (ABC) = aire (MNP)-3*3s=16s-9s=7s. Autrement dit S=7s ou s/S=1/7.
Enfin, merci à tous de votre participation et bravo !!
Prochaine énigme en parlementation auprès du conseil des sages, un peu de patience.
 Eh oui !! Je m'en étais aperçu depuis samedi midi !!
Eh oui !! Je m'en étais aperçu depuis samedi midi !!
Une simple erreur d'inattention dans le rapport des triangles semblables (1/2 au lieu de 3/4) .. et adieu le "sans faute" pour ce mois ..grrrrrrrrr!

 Jolie solution. Bravo à smk pour l'idée
Jolie solution. Bravo à smk pour l'idée 
Dommage pour cette bévue Nofutur2. Effectivement personne n'est à l'abri  ...
...
Sinon, quelqu'un aurait-il la bonté de m'aider à obtenir une démonstration propre ?
Il me manque Z,D,I alignés (sans passer par la méthode analytique).
J'ai essayé avec des parallélogrammes ou les barycentres mais sans succès...
 Pas évident ta question manpower !!
Pas évident ta question manpower !!
J'ai essayé mais je n'y arrive pas . Si tu décortiques la solution de Puiséa, il l'admet plus ou moins en supposant, lors de son partage final en 16 triangles que :
- la droite qui joint le milieu de AB2 et le tiers de BN passe par B'.
- la droite qui joint le milieu de AB2 et le tiers de CI passe par A'.
- la droite qui joint le milieu de CI et le tiers de BN passe par C'.
Et pourtant c'est vrai!!!
Il n'y aurait pas un probleme dans ta reflection car la somme de tes aire ABC=DEF+CBC'+ABB'+ACF=7 est incorect.l'aire de ta somme depasse l'aire de ABC pourrai tu mexpliquer
 Oui ce n'est pas franchement évident ! Tu as raison Nofutur2.
Oui ce n'est pas franchement évident ! Tu as raison Nofutur2.
Mais merci beaucoup d'avoir essayé 
Si finalement quelqu'un peut trouver une solution à ce problème... nous serons au moins trois à être délivré (Nofutur2, majuju et mézigue).
Nouveau sur ce forum, je viens de découvrir l'énigme 80.
Apparemment, personne n'a pensé à se ramener au cas où le triangle ABC est équilatéral.
C'est possible en appliquant à la figure initiale une transformation affine qui transforme ABC en un triangle équilatéral. Comme cette transformation conserve le rapport des aires des triangles, il suffit de faire la démonstration sur la figure transformée.
Avec ABC équilatéral, c'est plus facile.
Par exemple, on peut considérer le centre O de ce triangle et regarder les transformés des divers points par la rotation de centre O et d'angle 2Pi/3. On en déduit que le triangle qui nous intéresse (DEF) est globalement invariant par cette rotation, donc qu'il est équilatéral de centre O.
Pour finir, on peut reprendre la démonstration de Puisea, qui devient plus claire (il y a une multitude de triangles équilatéraux).
Ou bien on exprime le vecteur OE en fonction de OA et OB, puis le carré de sa norme en fonction de OA^2. On trouve OE^2=OA^2/7.
C'est aussi le carré du rapport de similitude entre le petit triangle et le grand, donc le rapport des aires.
Nombre de participations : 0
Temps de réponse moyen : 23:32:54.