Inscription / Connexion Nouveau Sujet
Compter les carrés dans une suite
Bonjour à tous 
Un petit bijou arithmétique à résoudre pour les fêtes sans IA ou autre machinerie .
On considère la suite d'entiers : 6 , 69 , 696 , 6969 , 69696 , 696969 , …
Parmi les termes de cette suite , y a-t-il une infinité de carrés parfaits ? Si non , combien y-en-a-t-il ?
Comme toujours on s'amuse sans abuser du blankage 
Imod
Bonjour,
une indication pour limiter la recherche, le nombre de 6 doit être un multiple de :
 Cliquez pour afficher
Cliquez pour afficher@Fabo34
Tu as parfaitement traité le cas ou le nombre de chiffres est impair , on utilise simplement la vieille règle de collège pour la divisibilité par 2 on regarde le dernier chiffre , par 4 les deux derniers , par 8 les trois derniers …
Le cas pair est un peu plus compliqué . La formule sommatoire que tu donnes est un bon point de départ mais après il ne faut pas se fixer sur 101 . le nombre avec n pair doit être un carré , il n'y a pas de grosse astuce qui tue le problème mais un peu de travail sur les modulos que tu as commencé à faire .
Encore un peu de courage 
Imod
Merci Imod. J'ai peut-être avancé un peu:
Les 2 parenthèses sont premières entre elles. Or ne peut pas être un carré car
. Et c'est
qui est multiple de 3 et qui vient compenser le facteur 3 du dénominateur. Les 2 parenthèses sont alternativement l'une ou l'autre multiple de 11. Donc mis à part la facteur 11 qui pourrait devenir "carré" par la simplification du facteur 11 au dénominateur, les autres facteurs de
ne peuvent donc pas être des carrés.
Mais il y a toujours ce 23 qui vient poser problème . Faut montrer qu'il y a d'autres facteurs premiers autres que 23 et 11 lorsque 23 est présent, comme par exemple dans . Là je sèche ...
La construction de Imod mérite une légère soustraction
exemple pour n=5 -->
pour les puissances impaires il faut déduire 3/11.
Si on prend le conseil de jandri il faut que le nombre de 6 soit
un multiple de 3 que l'on trouve pour les puissances de n telles
que 5+6k (ce qui au passage annule mon idée de 8348471......
et valide 264001836........),on doit bien appliquer la déduction de 3/11.
Si ça peut faire avancer.....
@Imod : Je viens de faire le rapprochement. Car ça fait 3 ans que je découvre ce théorème découvert par Fermat:
ne contient que des facteurs premiers congrus à
lorsque n est premier, ainsi que n lorsque n divise x+y.
Donc a priori 23 ne peut plus jamais apparaître dans pour des puissances supérieurs à 11!
Et pour des puissances 11 fois 3, 5, 7, alors pas de facteur 23 possible puisque:
Pendant que fabo34 travaille sur les congruences ,j'essaie de
chercher quel exposant fournira le deuxième carré 
La formule d'Imod et la remarque de jandri donne:
avec k=1 on obtient bien 69 696 et sa racine 264
avec k=4 on obtient 69 696 969 696 969 696 969 696 969 696
et sa racine 264 001 836 540 903 .0 mais hélas 5772934...
Il va falloir chercher plus loin..........
Finalement ,j'espère que fabo34 trouvera la preuve qu'il n'y a pas d'autre solution en partant des modulos de la fin d'un candidat 9696.
Donc Imod est un coquin en nous parlant d'infinité 
bonjour @dpi,
A priori c'est (presque) terminé. Il n'y a pas d'autres carrés que 69696=264². Je fais un petit résumé:
_ pour les termes pairs, il n'y a que 69696=264² à cause de la 2-valuation qui vaut 5 pour les termes suivants.
_ pour les termes impairs, il n'y en n'a pas. Car ils s'écrivent:
.
Or le terme ne peut pas être un carré (car congru à 2 modulo 3) . Il faut juste s'assurer que si 23 apparaît dans les facteurs premiers, alors il n'est pas tout seul. Or un théorème sur la somme de puissances d'exposant premier assure que 23 n'apparaîtra qu'un seule fois dans l'expression
. En l'occurence pour n=11 (
). Mais dans ce cas, on aura en même temps 11² dans les facteurs premiers, car 10+1=11. Or ce 11² va être divisé par 11, donc il sa valuation dans 969696969696969696969 sera ne sera que de 1 . Pas obligé la peine de décomposer ici en facteur premier.
je pense qu'il y a plus simple comme argument, car lmod a donné à voir la formule avec n pair
La formule de Imod avec n pair donne une valeur entière mais pas pour les nombres recherchés tel 69696 pour les quels n=5+6k
dpi: il me semble que la formule ne s'applique que pour les termes se terminant par 9, à savoir les 96969... mais pas ceux se terminant par 6
Nous sommes d'accord .
On sait par exemple que le seul carré parfait se termine par 6 donc un n impair.
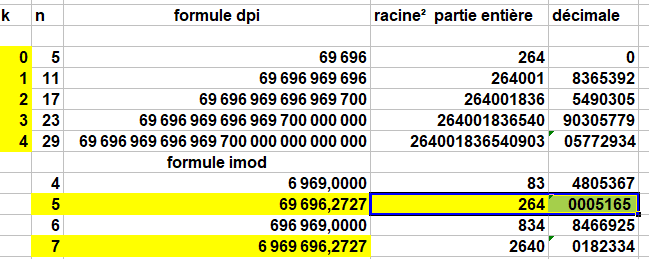
dpi : Les formules qu'on utilise ne s'applique qu'à la sous-suite 6969... Imod indique la forme avec n pair. Moi j'utilise plutôt l'expression
avec n premier pour ensuite factoriser
Mais ça ne s'applique pas à la sous-suite 696... tu ne peux pas l'utiliser pour ton tableau
dpi: je viens de tilter. Peut-être me signifies-tu que j'oublies des cas, justement avec n pair dans ma formulation, et pas seulement impair premier. Du coup il reste encore des cas à couvrir ... 

Imod, vient à notre rescousse !
Bon réveillon à tous.
Joyeux Noël,
J'ai eu l'idée inverse:
1/quelle que soit la construction de la suite la racine débutera par 264 ou 834.
2/en se fiant à l'indication de jandri elle se terminera par 6
3/ le début sera donc 264
4/le dernier chiffre d'une racine entière sera donc 4 ou 6
5/en testant les fins possibles on trouve rapidement 264-->69696
6/on peut tester 
j'arrive à 26 400 183 654 090 305 772 934 254 à la limite de mon bidule ; dont le carré est le plus "proche"
je postule donc que 264 est la seule réponse .
Mais l'approche de fabo34 semble propice
Mais c'est le théorème des 2 carrés, bien sûr! Ça tombe bien, il est aussi appelé théorème de Fermat de Noël !! , donc
.
Cette fois je pense que tous les cas sont couverts 
Oui , il y a de nombreuses façons d'obtenir le résultat avec les modulos . Personnellement j'étais parti de et ensuite il y a quatre cas :
: regarder modulo 11 .
: regarder modulo 8 .
: regarder modulo 8 .
: regarder modulo 8 .
Imod


