Inscription / Connexion Nouveau Sujet
Concours : mes mathématiques sur une étagère, 3e édition
Bonjour à tous
je CIJM vient de reconduire ce concours aujourd'hui même. La date limite des réponses est fixée au 22 mai. Cela se passe ici :![]()
Les liens vers les topics des éditions précédentes :
2010 : ![]() Concours CIJM : Mes mathématiques sur une étagère
Concours CIJM : Mes mathématiques sur une étagère
2011 : ![]() Concours "Mes Mathématiques sur une étagère" : 2ème édition
Concours "Mes Mathématiques sur une étagère" : 2ème édition
Les quelques énigmes que j'ai pu voir ont l'air bien corsées.
Il y a eu comme un raté au niveau du titre. Si un modo pouvait le rendre plus explicite, comme "Concours : mes mathématiques sur une étagère, 3e édition". Merci d'avance
* Tom_Pascal > C'est fait  *
*
Bonjour à tous,
J'ai posé deux questions aux organisateurs de ce sympathique concours. Je vous livre les réponses telles quelles.
Question 1 au sujet de l'énigme "Ce lemme éternel" :
Suffit-il de trouver une phrase qui réponde aux critères ou bien faut-il qu'elle utilise le plus de caractères possibles ?
Réponse CIJM : En fait, le principe de cette question est qu'elle sera considérée subjectivement par un jury. Donc la seule contrainte est celle écrite, mais plus ce sera original et/ou pertinent, plus la réponse aura de points.
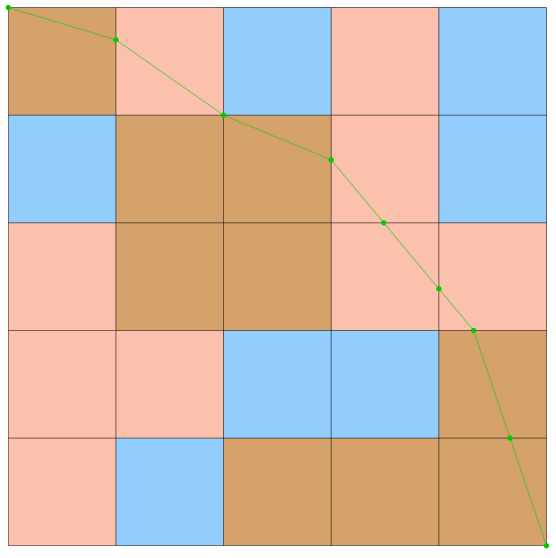
Question 2 au sujet de l'énigme "Fourmi non-euclidienne" :
Quelle est la vitesse de la fourmi quand elle marche sur la frontière entre deux zones de couleurs différentes ?
Réponse CIJM : La frontière est de largeur nulle.
En espérant que ça vous soit utile. 
Moins d'enthousiasme que pour la chasse au trésor. Sans doute dû au fait que l'on ignore la justesse des réponses jusqu'au dénouement. Pour ma part j'ai répondu à tout sauf à celle de créativité. Je risque de manquer de temps demain et ce n'est pas dit que j'y parvienne. Pour les autres j'ai quand même quelques doutes étant donné les différences de difficulté que j'ai ressenties. Échange de réponses possibles après la clôture pour ceux qui le souhaitent.
@Flanders:
Après la cloture ce soir, je serais curieux de connaître la réponse à "la science de l'hypothése".
Il me semble que c'est un cryptogramme assez difficile et j'ai essayé en vain de le résoudre.
bilbo.
Du retard semble être pris. Pour la chasse au trésor l'un des auteurs avait clôt manuellement le serveur. Ca m'arrange plutôt dans la mesure où j'ai enfin pu valider un texte et une image.
Concours terminé. Pour le cryptogramme il s'agissait d'une citation issue de "La science et l'hypothèse". Pour décoder il fallait regrouper les lettres par paquet de 5 et inverser le sens de chaque paquet.
Ce qui donne
Il n'y a pas de temps absolu ; dire que deux durées sont égales, c'est une assertion qui n'a par elle-même aucun sens et qui n'en peut acquérir un que par convention.
Personnellement, vu la longueur des premiers mots du texte à décrypter, et vu le " n' " au début, j'ai pensé que le texte commençait par "il n'y a pas".
J'ai cherché le texte de Henri Poincaré "la science de l'hypothèse".
Une recherche sur "il n'y a pas" m'a donné aussitôt la solution, en me basant sur la longueur des mots.
Après j'ai compris comment ce texte avait été crypté...
J'ai aussi répondu 294 secondes, sans prouver que l'on ne pouvait pas faire mieux ! En prenant le repère cartésien tel que A=(0,0), B=(5/5,5/5), j'ai pris un chemin passant par C=(2/5,1/5). Pour le reste du chemin j'ai appliqué la loi de la réfraction de la lumière de A à C d'une part, de C à B d'autre part.
Pas bête, je m'étais pris la tête pour trouver l'angle optimal en minimisant la distance en prenant les angles d'incidence et de réfraction pour paramètres, ce qui revient à redémontrer la loi de Snell-Descartes il me semble. Perdu dans mes calculs je me suis finalement rabattu sur Geogebra, qui permet au moins de tester plusieurs chemins. Peu rigoureux mais assez efficace pour le coup.
Bien joué Masab et Flanders, vous avez été plus rapide que moi. J'ai trouvé un temps de 296 secondes. J'ai du prendre une mauvaise option dans le choix du chemin...
Bon en attendant les réponses officielles, voici quelques unes des miennes :
- anneau 10 pour hanoi
- 5 étapes pour le boulanger
- 24 pentagones de souvenir
- 326 dominos
- proba de 20%
- genre 81 pour l'éponge de Menger
- 16917 minutes pour le problème des trois corps
Voilà, n'hésitez pas à confirmer ou l'inverse.
Je suis d'accord avec Flanders sauf
- 4 étapes pour le boulanger
- pour le problème des trois corps, j'ai oublié de tenir compte du rayon de la terre ! Après rectification, je trouve 21416 minutes
Par ailleurs je trouve
- 120 pour "de toutes dimensions"
- "De toutes dimensions" c'est bien l'exo avec le grand dodécaèdre étoilé ? Personnellement j'ai considéré les sommets externes qui forment un dodécaèdre régulier. J'ai compté 6 pentagones réguliers passant par chaque sommet. Étant donné qu'il y a 20 sommets, on obtient alors 6 *20 = 120 pentagones. Sauf qu'ainsi j'ai compté chaque pentagone 5 fois, en divisant par 5 j'obtiens 24.
- Pour le boulanger, le rayon du disque de départ est 1. A chaque étape on obtient un quart de disque dont le rayon est doublé. Cela serait sans doute plus clair avec une figure, je me suis longtemps demandé comment s'effectuait le pliage. Après 5 étapes j'obtiens un quart de disque de rayon 32 cm, recouvrant ainsi tout le carré.
- Pour les 3 corps j'ai effectué une équation aux différences finies, programmée en Python. Une erreur de ma part est tout à fait probable, je n'ai cependant pas oublié de tenir compte des rayons.
- "De toutes dimensions" concerne le volume d'un parallélépipède droit.
- Pour le boulanger, c'est effectivement 5 étapes la bonne réponse !
- Pour les 3 corps, j'ai utilisé F = m*gamma
Je me souviens plus de mes réponses sauf pour Hanoi où je me rappelle que je trouve l'anneau 3. Comment avez vous fait pour résoudre ce problème? Personnellement j'ai trouvé que l'on déplaçait chaque anneau de numéro n selon la formule 2^(n-1)+k*2^(n) avec k entier naturel. Pour résoudre le problème il fallait donc pour moi trouver l'anneau qui satisfaisait l'équation: "2012=2^(n-1)+k*2^(n) avec k entier naturel"
Les anneaux étaient rangés par ordre décroissant de taille. Ton anneau 3 correspond donc à notre 10.
Les résultats sont publiés sur le site du CIJM, "Résultat des concours et compétitions", rubrique mes mathématiques sur une étagère.
Ah merci pour l'info. J'avais fini par arrêter de consulter la page. Bon je finis 5e (4e égalité ?) avec 11,6 points. J'imagine que la décimale provient de l'épreuve littéraire.
Comme vous êtes classé dans les 5 premiers, avez-vous eu droit à un lot ?
J'ai bien peur que non, sinon vous auriez connu votre classement plutôt...
L'attribution des lots au concours "mes mathématiques sur une étagère" est toujours mystérieuse, ainsi que la nature des lots...
Dommage !
Si je suis récompensé je n'en ai pas encore été averti.
- L'édition précédente, deux jours après la fin de l'épreuve nous recevions un courriel indiquant notre classement ainsi que le nombre de prix attribués, il y en avait 12 dans la catégorie grand public.
- Lors de la chasse 2010, nous avions reçu le résultat une semaine après l'épreuve parisienne ainsi que le nombre de candidats primés. Il y en avait 5 et j'avais retiré mon lot sur place.
- Pour la chasse 2011, les palmarès des deux catégories étaient mis en ligne 13 jours après l'épreuve parisienne. Je crois que seuls les 5 premiers avaient été primés dans chaque catégorie.