Voici la figure

Bonjour, Qu'est-ce que tu ne sais pas faire ?
la figure ? la conjecture ? le calcul de l'aire du triangle ?

Oui et bien c'est bien, tu as trouvé que l'aire était maximal pour l'abscisse 2, c'est donc ça ta conjecture.

***message modéré***assimilé à du flood et/ou du multipost***

etudiantilois ne relance pas dans plein de topics pour recevoir de l'aide c'est tout à fait interdit !

mais je pense qu'il faut expliquer la conjecture non ? et ça je n'y arrive pas , je ne sais pas par où commencer

Prends un point courant de la parabole P(x;f(x))
calcule l'aire d'une triangle en fonction de x
trouve le maximum de cette fonction.

j'aimerais savoir comment tu as fait pour calculer l'aire pcq j'ai le même DM que toi sauf qu'on a pas à conjecturer par geogebra. Il faut juste déterminer les coordonnées de P pour que l'aire du triangle soit maximale et la je suis perdue depuis bien 2h maintenant

Bonjour,

tu veux dire comment il avait fait l'année dernière ?

en tout cas l'aire du triangle c'est formule connue surtout s'il s'agit d'un triangle rectangle !
reste qu'il faut écrire BQ en fonction de x et PQ en fonction de x
on obtient alors l'aire en fonction de x.

et cette fonction il faut ensuite l'étudier pour en déterminer le maximum

perso c'est pas Q mais H mais osef mdrr enfait le truc c'est que j'ai fais comme vous avez dis, càd faire l'aire du triangle avec P(x; f(x)) mais je trouve pas les bonnes images je comprends j'ai utilisé les coordonnées :
A=[(-6+x)(-2/9x^2+8)]/2
A=[4/3x^2-48-2/9x^3+8x]/2
A=-2/3x^2-1/9x^3+4/3x-24
et les images de la dérivée sont 6 et -2 et ça devrait être l'inverse ce qui veut dire que je me suis trompé dans mes signes un moment donné pcq les images qu'ln doit avoir sont -6 et 2 les opposés de celles que je trouve

non ça ne marche pas c'est le minimum local. Enfait j'obtiend tout l'inverse de ce qu'a obtenu l'autre personne sur geogebra qui a posé sa question sur son DM donc je pense que je me suis trompé au niveau d'un signe ou d'un x mais j'ai beau regarder partout je ne vois pas donc c'est forcément un problème dans la formule d'aire

** image supprimée **

scans ou photos de textes et de ses propres calculs (illisibles en plus) interdites
les calculs on les tape
le texte de l'énoncé on le tape.

sans les calculs (recopiés !) ... on discute dans le vide.

dsl je ne savais pas pour l'image et c'est illisible car j'ai fais ça vite fait vous faite jamais ça vous ? enfin bref après je l'ai écrit sur ma feuille et j'aurais pu l'effacer c'est vrai. Pour le reste je suis aussi perdue que vous. Non -2 donne le minimum et 6 le maximum : f(-2)=-28,4 ; f(6)=0 et donc 6 n'est pas un maximum. Regardez les résultats de la personne avec geogebra au début, vous allez voir, on a les mêmes résultats a l'exception qu'ils sont opposés

"qu'ils sont opposés", donc ce n'est pas les mêmes

pourtant c'est le même énoncé !!
(si différent il faut le recopier !! pas le photographier seule une éventuelle figure est autorisée en image)

l'utilisation ou non de geogebra ne change rien à l'affaire, le résultat ne dépend que de la définition de la fonction et du triangle et pas des outils utilisés (géogebra ou papier crayon)
alors cherchez l'erreur ...

calcul de l'aire du triangle en fonction de x :
A=-2/3x^2-1/9x^3+4/3x-24 est faux
d'ailleurs il est évident que cette aire devrait s'annuler en x = -6 et x = +6 (quand Q, alias H, est en A ou B, hauteur du triangle = 0)
ce qui est faux
pour x = 6 ton aire donne -2/3 * 6^2 - 1/9 * 6^3 + 4/3 * 6 - 24
= -24 - 24 +8 - 24 = -64 !!
de plus ton aire est partout < 0 dans [-6; +6] ce qui la fiche mal pour une aire !


A=[(-6+x)(-2/9x^2+8)]/2 faux ça c'est l'aire d'un autre triangle (cause de l'inversion de tes résultats)
et en plus avec une erreur,
en effet ton côté (ton -6+x) serait négatif pour x dans [-6; +6] ce qui la fiche mal pour une mesure de longueur ! (c'est la cause de ton aire <0 )
de plus la dernière ligne de ton développement est fantaisiste (ce n'est pas la division par 2 du numérateur de la ligne précédente) mais ça je suspecte plutôt une erreur de recopie vu que tu prétends correctement f(6) = 0

avec ton aire négative cela inverse la notion de maximum / minimum
en effet les maxima de f(x) sont des minimas de -f(x) et vive versa !

je me suis trompée dans mon recopiage, c'est pas 4/3x mais 4x. Pour la division j'ai simplement tout divisé par 2 et c'est forcément vrai les réponses que j'ai trouvé pcq j'obtiens les racines opposés de ce qu'il faut trouver. Après pour la formule de l'aire j'ai sûrement faux c'est ce que j'ai dis plus haut et ça ne m'aide pas ce que vous  dites.

si
déja en corrigeant ton coté de -6+x faux en ce que doit être la bonne expression de la mesure du segment concerné
et tu verras que tout rentrera dans l'ordre ...



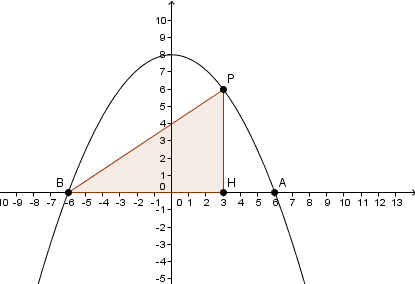
la mesure de BH c'est xH - xB pas xH + xB
la mesure de HA (si c'est "l'autre" triangle, PHA au lieu de PHB) c'est xA - xH, pas xH - xA
aucune des deux ne donne -6+x

non mais vous avez compris ce que je voulais dire, et quoi qu'il arrive, B=-6 donc dans ce cas que ce soit xH-xB ou xH+xB ça ne change pas grand chose mais je sais que c'est par rapport à cette formule déjà j'ai mis du temps avant de trouver ce que je devais mettre à la base et en hauteur
Je vais essayez de me débrouiller et merci

c'est pas croyable d'être têtu à ce point !!
le calcul de la mesure de la base est faux et c'est la source de tous tes ennuis
(en plus de l'absurdité de croire que si on ne trouve pas exactement pareil que le résultat attendu c'est que c'est "vrai" )

avec B = -6 et le triangle BPH, BH = xH - xB = x+6 et pas 6-x
pfff

xH-xB = x-(-6) = x+6
ou xH+xB = x +(-6) = x-6 (mais ça ne rime à rien xH+xB)
tu trouves que x+6 et que x-6 c'est pareil ????
et de toute façon ça ne fait pas non plus ton 6-x

je ne suis pas têtu je me suis juste trompée et je ne savais pas où et je ne comprenais pas ce que vous disiez donc voilà et pour le xH-xB j'avoue c'est pas la même que xH+xB j'avais pas fait le -+-=+ voilà et donc grâce à vous tout est bon donc je vous remercie beaucoup d'avour usé de votre temps
La stupide