Inscription / Connexion Nouveau Sujet
Coordonnées d'un projeté orthogonal
Bonjour ,
Je suis bloqué sur un exercice qui est le suivant :
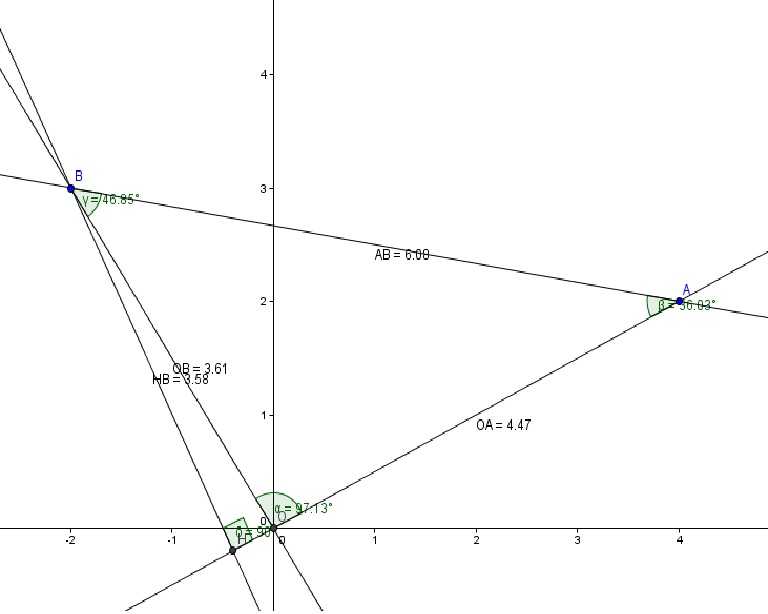
Soit un repère orthonormé (O;i;j)
Calculer les coordonnées du projeté orthogonal de H de B (-2;3) sur la droite OA où A a pour coordonnées (4;2)
J'ai tracé la figure sur geogebra mais je ne comprend pas comment trouver les coordonnées du point H.
Je pensais passer par les angles mais je m'en sort plus ...
Bonjour,
si H est le projeté orthogonal de B sur OA alors tu peux dire que le triangle BHA est rectangle en H donc que BH²+HA²=AB² et que H appartient à la droite OA ; tu dois donc poser (x,y) les coordonnées de H et écrire les deux relations concernant H en fonction des coordonnées de A, B et H ...
Oui c'est ce que j'ai fait mais alors avec l'equation AB²=BH²+HA² on a une relation avec des distances et non des points en fonction de x et y ...
tu as une relation avec des x et y tes deux inconnues ensuite tu sais que H appartient à la droite OA ce qui te donne une relation entre x et y tu auras donc deux équations à deux inconnues...
commences par me donner le détail de la relation AH²+HB²=AB²
ensuite écris l'équation de la droite OA
Pour AH²+HB²=AB² On a : (Xb-Xa)²+(Yb-Ya)² = ((XH-XA)²+(YH+YA)²)+((XB-XH)²+(YB-YH)²)
Les racines se simplifie avec le carré des vecteurs dans la formule de pythagore.
et la je trouve cette équation trop complexe...
et pour l'équation de la droite OA j'ai y=(1/2)x
Ok pour l'équation de (OA)
tu connais les coordonnées de A ainsi que celles de B, tu peux donc exprimer AH² et BH² en posant les coordonnées de H=(x,y) et tu peux donner également AB²
Oui mais si je remplace simplement dans l'équation j'obtiens :
(-2-4)²+(3-2)²=(Xh-4)²+(Yh-2)²+(-2-Xh)²+(3-Yh)²
alors voilà ce je j'obtiens :
maintenant tu peux continuer en disant que HB²+HA²=AB² tu développes et tu regroupes ensuite tu te sers de la relation et tu remplaces y par l'expression en fonction de x puis tu résous l'expression ainsi obtenue en fonction de x
Alors je suis d'accord c'est exactement ce que j'ai fait juste ci-dessus.
en remplacent y par (1/2)x j'obtiens au final une équation du 2nd degré : 37=3x²-9x+33
donc 0=3x²-9x-4
je calcul delta et j'obtiens deux solutions x1= -0.39 et x2=3.39
approximativement .
Je choisis donc quel solutions pour Xh ? logiquement c'est -0.39 car la droite OA est croissant et le point H est négatif en Y et X.
Par déduction de Y=(1/2)Xh je trouve Y=-0.195
est-ce juste ?
j'ai tracé sur le logiciel geogebra la figure qui après peut me donner les coordonnées des points en en tracer le projeté orthoganal H je trouve comme coordonnéeH(-0.4;-0.2)


