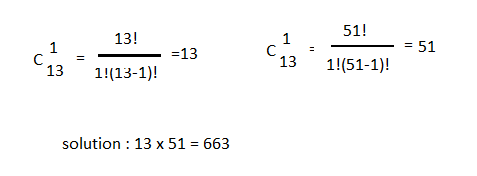Inscription / Connexion Nouveau Sujet
Demande de correction éventuelle de probabilité
Bonjour,
Y a t-il une âme charitable pour vérifier cet exercice, dont je ne suis pas certain du résultat obtenu.
Fichier jpeg placé en fichier joint.
Je crois qu'en jpeg, il est possible d'y ajouter des remarques.
Je ne sais pas mettre cette image plus nette(qualité très limitée sur le site)
Merci de bien vouloir me renseigner.
****Tilk_11> Image supprimée, pas de scan de document...tu dois recopier ton énoncé ! ****
Re,
Mais, comment faire quand on a des formules et schémas qui expliquent le solution proposées alors !
Les fichiers attachés ne sont plus admis?
Merci
Re,
C'est un problème de probabilité.
Un jeu de cartes, de 52 cartes, on tire 2 cartes
Calculer
la probabilité de tirer 1 carreau( pas plus d'explication)
La supposition faite, est qu'il n'est possible de tirer qu'un seul carreau (juste ou pas juste?)
1ère solution : en 1ère main je tire 1 carreau soit 13/52
en 2ème main, je tire 1 carte quelconque soit 51/51
solution : 13/52 x 51/51 = 663/2652 (schéma joint est carreau-carte)
autre solution qui ne donne pas la même réponse.
2ème solution : en 1ère main , je tire 1 carte quelconque soit 52/52
en seconde main, je tire 1 carreau soit 13/51
solution : 52/52 x 13/51 = 676/2652 (schéma joint est carte-carreau)
Pas sûr que les solutions soient bonnes.
question 1 : Demande de vérification (avec correction éventuelle)
question 2 : Est-il logique que les 2 solutions soient différentes?
Les dessins sont-ils arrivés?
Merci de votre aide.

re,
L'énoncé est de calculer le probabilité d'avoir 1 carreau ( ni plus ni moins)
tout en tirant 2 cartes d'un jeu de 52 cartes. 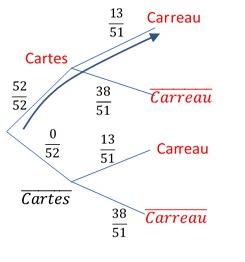
Re,
Attention,
Dans le cas que j'ai posé, on ne peut avoir qu'une seule carte de carreau et la suivante doit être une carte quelconque (mais pas un carreau).
on tire 1 carreau et une autre carte (mais pas de carreau)
voilà le soucis.
Dans le cas que j'ai posé, on ne peut avoir qu'une seule carte de carreau et la suivante doit être une carte quelconque
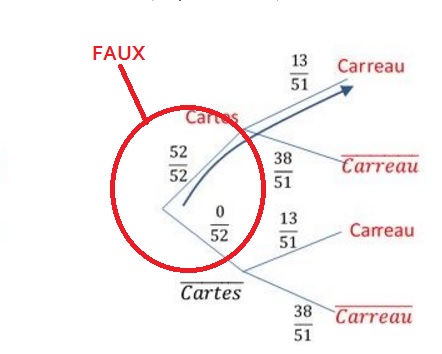
Faux.
Soit la première carte est un carreau, et la seconde dans ce cas ne doit pas l'être.
Soit la première n'est pas un carreau, et dans ce cas la seconde doit l'être.
Il y a donc 2 événements qui remplissent la condition.
voilà le soucis.
Aucun souci.
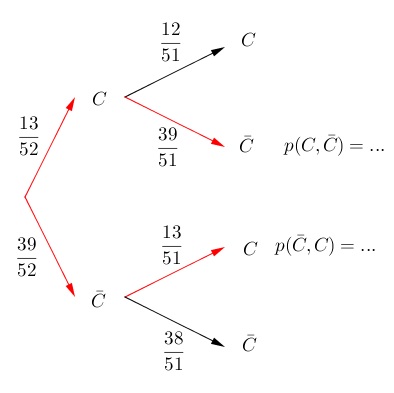
Les 2 "chemins" en rouge dans l'arbre ci-dessous remplissent cette condition.
Il n'y a plus qu'à faire les calculs.
Bonjour
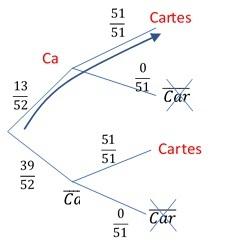
Ton arbre avec 2 issues :
On tire une carte ou on ne tire pas une carte, tu comprends pourquoi c'est une fausse piste que tu suis ?
Il n'y a pas que les probabilités qui sont fausses ! Les issues sont aussi fausses.
Il faudrait bien définir l'événement qu'on appelle C
C'est on tire une carte ou on tire une carte qui est un carreau ?
Tant qu'on ne définit pas correctement les éléments utilisés on n'est pas crédible dans sa démonstration
L'événement C n'étant pas vraiment défini, tout est possible.
J'ai vu le sujet avant que l'image soit supprimée. Il y avait des notions de combinaisons écrites avec C au lieu de ()
Cela me fait penser à un vieux sujet sorti des catacombes ou à un sujet venant de l'étranger et dans tous les cas, il est difficile de savoir quelles notions on peut utiliser pour résoudre cet exercice.
Un même calcul donnerait 2 résultats différents ? Dans quel galaxie ?
Tu comprends ce que tu écris ?
Mais, le schéma que vous aviez proposé, je l'avais déjà fait.
Je n'y peux rien, si la dernière réponse ne vous satisfait pas.
Montrez -moi votre solution, alors.
1ère solution : en 1ère main je tire 1 carreau soit 13/52
en 2ème main, je tire 1 carte quelconque soit 51/51
solution : 13/52 x 51/51 = 663/2652 (schéma joint est carreau-carte)
raisonnement faux
car lors de ce que tu appelles la 2e main si tu tires dans 51 cartes, tu peux encore obtenir un carreau, et dans ce cas, tu aurais 2 carreaux et non 1 carreau
donc raisonnement à abandonner
2ème solution : en 1ère main , je tire 1 carte quelconque soit 52/52
en seconde main, je tire 1 carreau soit 13/51
solution : 52/52 x 13/51 = 676/2652 (schéma joint est carte-carreau)
2e raisonnement tout aussi faux car tu peux aussi obtenir 2 carreaux par ce genre de tirages
donc raisonnement à abandonner également
quant à
D'accord que la seconde carte peut-être un carreau.
Mais, fonction de la réponse faite en classe ( c indice 51 exposant 1 = 51), est considéré comme une carte parmi les 51 cartes restantes
Ce qui donne comme résultat final 13 x 51 = 663/2652
Ce qui voudrait dire que l'on peut avoir 1 carreau et 1 carte quelconque.
Alors, comment obtenir 663 comme résultat ?
(suivant votre arbre, c'est pas possible)
La seule façon d'avoir 663, est 1ère branche 13/52(carreau) et 2 ème branche 51/51(carte quelconque restante, dont 12 carreaux + 39 autres).
J'espérais avoir comme réponse 663 , mais apparemment vous n'êtes pas très d'accord.
Alors qui a la bonne réponse?
Merci
Bonjour Mistral.
Les cartes se répartissent en deux groupes :
les carreaux : il y en a 13
celles qui ne sont pas des carreaux (cœurs, piques, trèfles) : il y en a 39 : les "autres".
Il ne faut pas confondre le deuxième groupe avec les cartes quelconques, qui sont 52.
Première possibilité : tirer un carreau, puis une "autre".
La probabilité de tirer d'abord un carreau est 13/52.
Cela étant fait, il reste 12 carreaux et toujours 39 "autres" sur 51 cartes en tout.
La probabilité de tirer ensuite une "autre" (qui ne soit pas un carreau) est 39/51.
La probabilité d'un tel tirage est donc 13/52 * 39/51 = 507/2652.
Deuxième possibilité : tirer une "autre", puis un carreau.
La probabilité de tirer d'abord une "autre" est 39/52.
Cela étant fait, il reste toujours 13 carreaux et 38 "autres" sur 51 cartes en tout.
La probabilité de tirer ensuite un carreau) est 13/51.
La probabilité d'un tel tirage est donc 39/52 * 13/51 = 507/2652.
Il est évident que ces deux possibilités ne peuvent pas se réaliser toutes les deux à la fois. La probabilité que l'une d'entre elles se réalise est 507/2652 + 507*2652 = 1014/2652 = 13/34 (environ 38,2 %).