Inscription / Connexion Nouveau Sujet
Démonstrations produit scalaire
Bonjour tout le monde !
Je n'arrive pas du tout à faire les démonstrations de mon devoir, je vous montre :
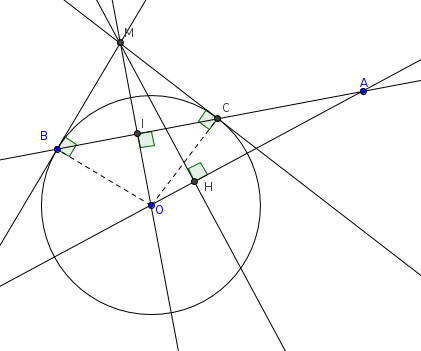
J est un cercle de centre O et de rayon R. La droite d passe par A et coupe le cercle en B et C. Les tangeantes menées par B et C au cercle J se coupent en M. La droite (OM) coupe (BC) en I et M se projette orthogonalement en H sur (OA)
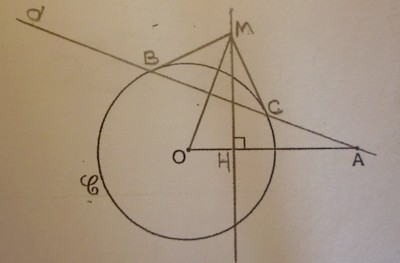
Démontrer que :
OH.OA = OM.OA = OM.OI
Démontrer ensuite que :
OM.OI = OM.OB = OB²
En déduire OH.OA = R²
Je n'ai jamais trop compris les produits scalaires "bruts", sans calculs, j'aimerai un peu d'aide. Merci !
Bonjour, OM.OA=(OH+HM).OA=OH.OA+HM.OA mais HM est perpendiculaire à OA donc HM.OA=0 et donc OM.OA=OH.OA
C'est pareil pour OM.OI=OM.(OA+AI)=OM.OA+OM.AI=OM.OA
Essaye de continuer sur le même principe : décomposition avec Chasles et élimination des produits qui sont avec deux vecteurs perpendiculaires.
bonjour
ça, c'est issu directement de la définition du produit scalaire que tu as vu en cours
montre ensuite que
ensuite
c'est issu directement de la définition du produit scalaire que tu as vu en cours
bonjour
j'ai complete ta figure et donc se calcule en projetant A sur (OM) ou M sur (OA)ainsi
et dans cette somme il y a un produit scalaire de deux vecteurs orthogonaux
donc ....
et dans cette somme il y a un produit scalaire de deux vecteurs orthogonaux
donc ....
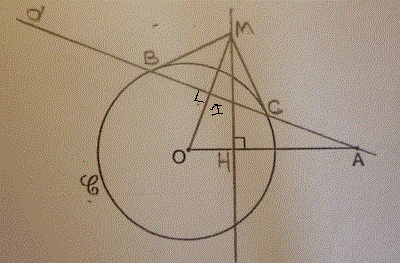
Merci beaucoup pour votre aide, et merci pour ta figure dhalte. Je commence à mieux comprendre comment ça marche maintenant. Je vais essayer de faire la démo pour OM.OI = OM.OB = OB², même si je sens que je vais avoir un peu de mal ^^'