Inscription / Connexion Nouveau Sujet
Des 0, -1 et 1 dans un tableau
Bonjour à tous, je suis en 3ème à Paris et je fais partie d'un dispositif qui permet de pouvoir rejoindre le lycée Louis-Le-Grand. Nous avons eu le premier cours de mathématiques et le professeur nous a donné comme devoirs plusieurs exercices. Voici l'énoncé du premier:
Dans un tableau de taille 3x3, on place des -1, 0 et 1.
Montrer que parmi les huit sommes définies par les colonnes, les lignes et les diagonales, deux sont égales.
Merci d'avance pour votre aide.
ben si c'est "internet" qui te fait tes exos, tu ne risques pas d'entrer et de suivre à Louis-le Grand....
donc va falloir remonter tes manches, réfléchir,faire des propositions, tester...etc....et en dernier recours appeler au secours ! mais une fois que tu pourras dire ce que tu as cherché et pourquoi ça fonctionne pas ou mal....
D'accord mais pour la répartition des chiffres, il doit y avoir trois (-1), trois 0 et trois 1 ou bien ... ?
Bonjour,
Je te suggère de te poser la question suivante :
"Quelles valeurs peut avoir chacune de ces sommes ?"
"Combien de valeurs différentes cela représente-t-il ?"
Chaque case vaut -1, 0 ou +1.
La somme des 3 cases peut-elle être 4 ? Non !
Mais 0 est possible... et quelles autres valeurs ?
Je suis entrain de chercher mais j'ai compris l'idée. Merci je vous donne le résultat si je finis par y arriver
Si tu ne disposes que de 7 valeurs à distribuer à 8 destinataires, au moins 2 recevront la même chose.
Quand 7 sont "servis" différemment, le 8ème reçoit la même chose qu'un des sept déjà servis.
Dans une famille de 3 enfants au moins 2 sont de même sexe !
Là où l'énoncé n'est pas "clair", c'est qu'il faut préciser au moins 2 sommes sont identiques, il peut y en avoir davantage !
Bonsoir,
Tu as pourtant bien avancé :
Tu as 6 totaux horizontaux et verticaux + totaux (diagonales)
Comme en variant au maximum les combinaisons tu en trouves 7
il y aura forcément deux totaux identiques.
A noter que tu peux même en trouver 7 (0) et le dernier 3 (1+1+1)
Juste, est-ce que tu peux ré-expliquer la dernière stp. J'ai pas très bien compris.
[PS: as tu trouvé la solution, toi ?]
Bon
Tu remplis ton tableau de 9 cases en mettant au hasard 0,-1,+1
Tu fais les totaux horizontaux
tu fais les totaux verticaux
tu fais les totaux des diagonales
Cela te donne 8 totaux
Comme tu as calculé toi-même qu'il n'y avait que 7 possibilités
il y en aura donc un déjà compté. FIN
Mon observation est qu'il peut même y en avoir 7 identiques.
si tu répartis -1,0et +1 de façon homogène et dans ce cas
tu auras six 0 +un en diagonale ,l'autre totalisant 3
J
Est-ce que ça marche si je fais ça ? :
1 1 0
1 0 -1
-1 -1 -1
Sachant que les résultats obtenu sont trois (0), un (1), un (-1), un (2), un (-2) et un (-3).
Oui c'est bon, mais tu dois préciser que c'est un exemple
et que tu as prouvé qu' avec 7 possibilités et 8 totaux,
2 au moins seraient égaux
Ok mais au début j'ai cru qu'il fallait exactement 2 sommes qui soient égales, c'est pour cela que j'étais dans le doute.
Bonsoir à tous
Je trouve que l'énoncé n'est pas assez précis
faut-il avoir obligatoirement 3 fois les nombres 0, 1 et -1 ?
et est-ce : Montrer que parmi les huit sommes définies par les colonnes, les lignes et les diagonales, deux seulement sont égales.
car on peut avoir au maximum 8 sommes égales à 0 (carré pseudo magique) ou avoir dans un même carré par exemple entre autres 2 sommes égales à 0, 2 sommes égales à 1 et 2 sommes égales à -2
par contre on ne peut pas avoir 2 sommes égales à 3 et à -3
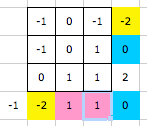
Je trouve également que l'énoncé n'est pas assez précis mais je dois rendre ce devoir et je ne verrai pas le professeur en question avant de devoir lui rendre.
tu dis dans ta rédaction comment tu as compris ton énoncé et tu le résous ainsi que tu l'as compris
quand il y a une ambiguité, c'est ainsi que l'on fait

 !
!
