Bonjour ,

Pouvez vous me corrigez ? et m'aider à faire la suite svp ?

ABCD désigne un rectangle tel que AB = 7,2 cm et BC = 5,4 cm.

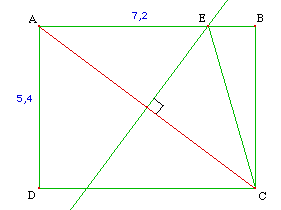
1) Dessiner en grandeur réelle, ce rectangle et sa diagonale [AC].

2) Calculer la mesure arrondie au degré de l'angle .

ABCD est un rectangle donc le triangle ADC est rectangle en D et on peut utiliser la trigonométrie.

tan ACD = coté opposé / coté adjaçant =  AD / DC  = 5.4 / 7.2  = 0.75

La calculatrice donne une valeur d'environ 36,869 ... ° .

L'angle mesure 37° ( au degré près).

3) Démontrer que les angles et sont égaux.

ABCD est un rectangle donc les droites (AB) et (CD) sont parallèles. (AC) est une sécante. Les angles et sont alternes-internes.

Si l'on a deux droites parallèles et une sécante alors les angles alternes-internes formés sont égaux.

Les angles et sont égaux.

4) La médiatrice du segment [AC] coupe la droite (AB) en E. Placer le point E et montrer que le triangle ACE est isocèle.

E est un point de la médiatrice du segment [AC].

Si un point appartient à la médiatrice d'un segment alors il est équidistant des extrémités de ce segment.

E est équidistant de A et de C donc EA = EC.

Si un triangle a deux côtés de même longueur alors il est isocèle.

5) En déduire une valeur approchée de la mesure de l'angle .


DCE = DCA + ACE
DCA = environ 37° d'après la premiere question
ACE = CAE car le triangle ACE est isocèle
CAE = ACD car les deux angles sont alternes-internes (voir question 3)
donc  ACE = ACD et ACE 37°
DCE = DCA + ACE 37 °  + 37 °   - DCE 74 °

Auriez vous une méthode plus courte celle là est tres longue ?

6)  a) en égalant les deux quotient trouvés au questions 2) et 3) on trouve l'équation : 35(90 - x ) 25 x
        résoudre cette équation sans justification

    b) en déduire la valeur commune des angles CEN et DEB arrondie au degrès près

Merci à tout ceux qui me corrigeront et aideront pour la question 6 A + tard