Inscription / Connexion Nouveau Sujet
distance d'un point à une droite
bonsoir, j'ai un exercice à faire mais je ne comprends pas ; voici l'énoncé
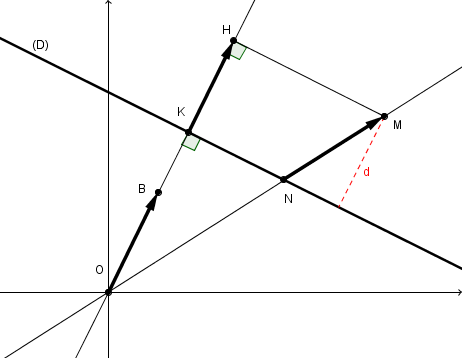
(O,i,j) un repère orthonormal . D la droite d'équation ax+by+c=0 et M est un point quelconque du plan de coordonnées (x,y) . on suppose que (OM) et D sont sécantes.
le but est de déterminer la distance de M a D.
B est le point de coordonnées (a,b). Le point N(x',y') est le point d'intersection de (OM) et D
K est l'intersection de (OB) et D
H est le projeté orthogonal de M sur (OB).
1) faire la figure
2) justifier que OB.NM= + - OBxKH
3) justifier que OB.NM= ax+by+c
4)justifier que KH= norme(ax+by+c)/)racine de a²+b²)
5) delta est la droite d'équation y=2x-1 et A le point de coordonnées (-8;3) . calculer la distance de A à delta.
pouvez vous m'aidez SVP
j'ai fait la figure et j'ai esayer de trouvé le 1) je trouve en utilisant la formule u et v 2 vecteur A,B,C 3pts u=AB et v=AC et H projeté orthogonal de C sur (AB) alors u.v=AH*AB mais je trouve : OB.NM=OHxAB
merci d'avance
2) OB.NM = OB*KH ? Le vecteur OB étant perpendiculaire à la droite D comme le vecteur MH, le vecteur NM se projette en HM dans la direction de cette droite, de sorte que je dirais
plutôt OB.NM = OB*HM .
Bonjour
je n'ai rien compris à tes explications
d'abord la 1 c'est juste faire "la" (une) figure avec des valeurs de a, b, x, y au hasard)
il n'y a aucun calcul
on doit justifier pourquoi le vecteur OB est orthogonal à (D) (cours) et on marque les angles droits sur la figure pour mieux y voir clair
ensuite la 2)
on utilise la propriété de la projection des vecteurs pour calculer le produit scalaire
dans ce que tu as écrit de l'énoncé il faut absolument distinguer ce qui est vecteurs et ce qui est nombre (mesures de longueurs)
je suppose qu'il était écrit :
justifier que
à défaut de savoir mettre des flèches (en LaTeX) tu écris "v" ou "vec" pour les vecteurs
vOB.vNM= +/- OBxKH
quelle est la projection du vecteur su la droite (OB) ?
terminé pour la question 2)
on passe à la question 3
cette question se résout en deux coups de cuillère à pot par la formule du produit scalaire avec les coordonnées des vecteurs
coordonnées de
coordonnées de
donc calcul "algébrique" de ce produit scalaire
et il se simplifie parce que N est sur D donc x' et y' satisfont à l'équation de (D)
exit question 3
question 4 :
on égale les deux expressions de la question 2 et de la question 3
question 5 : application numérique.