Inscription / Connexion Nouveau Sujet
DM fonction et triangle
bonjour, voivi mon exercice ;
Soit un triangle ABC tel que :
AB = 8 , AC = 6 et IC = 4, ou I est le milieu du côté [AB]. Le point G est le milieu de [IC].
f est la fonction qui à tout point M du plan associe le reel: f(M)= MA^2 + MB^2 - 2MC^2.
1) Démontrer que G est le barycentre de {(A,1) ; (B,1) ; (C,2)}.
2) Démontrer que f(M)= 4IC.GM + 1/2 AB^2 pour tout point M du plan.
3) Soit k un reel. On considère l'ensemble Ek des points M tels que : f(M) = k.
4) Determiner et représenter graphiquement les ensembles E0, E32 et E60.
5) a) Calculer BC.
b) Determiner le reel k tel que le point C appartient à l'ensemble Ek.
Voici mes résultats :
1) a + b + c doit être différent de 0. Vérifions : 1 + 1 + 2 = 4. Donc G est le Barycentre des points pondérés (A,1) (B,1) (C,2) tel que 1 GA + 1 GB + 2 GC = 0. Vérifions :
GA + GB + 2 GC = 1 (GA + GB) + 2 GC
I milieu de [AB] donc I isobarycentre de {(A,1) ; (B,1)} avec a+b = 1+1 = 2
donc GA + GB = (1+1) GI = 2 GI
D'ou GA + GB + 2 GC = 2 GI + 2 GC = 2 (GI + GC) = 2 * 0 = 0.
G est donc bien le barycentre de ce système pondéré.
2) D'après le théoreme de la médiane f(M) = 2 MI^2 + 1/2 AB^2 - 2 MC^2
= 2 MI^2 + 1/2 AB^2 - 2 ( MI + IC )^2
= 2 MI^2 + 1/2 AB^2 - 2 MI^2 - 4(MI.IC) - 2 IC^2
= 1/2 AB^2 - 4 IC (MI + 1/2 IC)
= 1/2 AB^2 - 4 IC (MG+GI+1/2 IC)
= 1/2 AB^2 + 4 IC.GM
= 4 IC.GM + 1/2 AB^2
4) Pour E0, f(M) = 4 IC.GM + 1/2 AB^2 = 4 IC.GM + 1/2 (AI+IB)^2
= 4 IC.GM + 1/2 AI^2 + AB + 1/2 IB^2
J'ai poursuivi mon calcul (qui est très long) jusqu'à obtenir = 4 [IM.IC -4]+AB + 16.
Et je suis bloquée. De plus je ne suis pas certaine que mon calcul soit exact et que j'ai pris la bonne voie pour répondre à la question. Pouvez-vous m'aidez ?
Et sinon est-ce que mes autres réponses sont exactes ?
pour le 1) si tu veux raisonner en termes de barycentres
G bary de C,2 et I,2
I bary de A,1 et B,1
comme 1+1=2, G bary de C,2 et de A,1 et B,1
I milieu de [AB] donc et
Je trouve qu'on pourrait en rester là pour résoudre la suite, mais ton énoncé veut introduire G, je ne sais pas pourquoi.
G milieu de [IC] donc et
Et, quitte à faire, autant ne conserver que le point G, mais là encore, il faut faire apparaitre G ET I. Bizarre, cet énoncé :
Et, pour finir, pourquoi alors ne pas faire intervenir les positions réelles des points données dans l'énoncé :
AB=8, donc
résolvons
on a immédiatement :
rappelons nous l'interprétation géométrique du produit scalaire :
soit H le projeté orthogonal de M sur (IC), alors nous avons entre le produit scalaire et les valeurs algébriques la relation :
si on choisit l'orientation d'un repère de(IC) tel que , alors puisque IC=4 d'après l'énoncé, on a
et notre relation vectorielle devient
Autrement dit, les points M qui répondent à l'équation sont ceux dont le projeté orthogonal H sur (IC) orienté répond à l'équation
Traitement du premier cas, tu pourras ensuite faire les autres
k=16
sur la droite orienté (IC) plaçons tel que
: les points
solutions de f(M)=16 sont ceux de la perpendiculaire à (IC) passant par ce point
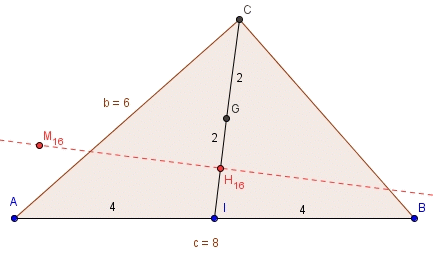
Merci beaucoup, J'ai trouvé pour les deux autres ensembles :
Pour E32 :
GH = 0.
Le point H est donc confondu avec le point G. L'ensemble E32 des point M tel que f(M) = 32 est donc la droite perpendiculaire à (IC) passant par G.
Pour E60 :
GH = 7/4.
L'ensemble E60 des points M tel que f(M) = 60 est donc la droite perpendiculaire à (IC) passant par H60.
Ensuite pour la question 5) :
a. En démontrant que le point appartenait au cercle de diametre AB, j'en ai conclu que le triangle ABC était rectangle en C. Ensuite j'ai appliqué le théoreme de pythagore et trouvé BC = 2 7.
7.
b. Je ne suis pas sûre de mon raisonnement :
Pour que C appartienne à Ek, le projeté orthogonal de M doit etre confondu avec C, donc GH = GC.
Avec IC.GC = k/4 - 8 ,j'en suis arrivée à la conclusion que k = 64 pour que C appartienne à l'ensemble Ek.
Est-ce exact ?
BC : correct
Pour E32 H=G
Pour E60, donc H entre G et C et GH=7/4
5) Le raisonnement pour trouver k est correct.
La valeur trouvée pour k est correcte.
Bravo



