Inscription / Connexion Nouveau Sujet
Dm Produit scalaire ,mecanique
Bonjour je rencontre beaucoup de probleme sur ce dem je ne comprens pas grand chose voila pourquoi je fait apelle a vous merci de votre aide .
enoncé :Un skieur remonte à vitesse constante une pente enneigée, tracté par une perche accrochée au câble d'un téléski, sur une
distance D entre 2 points A et B.
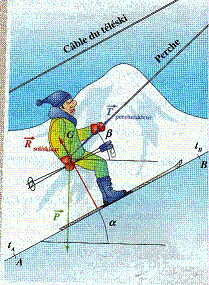
Il est soumis a 3 actions mécaniques concourantes en I, point d'intersection de la verticale passant par G (centre de
gravité du skieur) avec l'axe de la perche.
*Son poids (vecteur P),de norme P=mg, de direction verticale passant par G.
*l'action de sol sur les skis (vecteur Rsol/ski, perpendiculaire à la pente, car on peut négliger les frottements
du sol sur les skis.
*L'action de la perche sur le skieur (vecteur Tperche/skieur), dont on notera T la norme, dont la direction suit
l'axe de la perche.
La pente forme un angle de mesure alpha (en °,avec 0 "inférieur ou égal" a alpha "inférieur ou égal" a 90)avec l'horizontale.
La perche forme un angle de mesure beta ( en °, avec alpha<beta<90 ) avec l'horizontale.
Le travail de chacune des forces entre A et B est le produit scalaire du vecteur force par le vecteur AB: pour une force
par le vecteur F,Wab (vecteur F)=vecteurF.vecteurAB
Questions
1
a. Que peut-on dire du travail de la force vecteurRsol/ski.
b. Exprimer le travail du poids P en fonction de m,g,ABet de alpha. Quel est le signe de cos(alpha+90)?
Quel est le signe du travail du poids?
c.exprimer le travail du poid de l'action de la perche vecteur Tperche/skieur en fonction de T,AB,alpha et beta.
Quel est le signe de cos(beta-alpha) ? Quel est le signe du travail de Tperche/skieur.
2
Le skiur se déplaçant à vitesse constante, la variation de l'energie cinétique u systéme entre A et B est nulle. Or, d'aprés
le théoreme de l'énergie cinétique, cette variation est égale à la somme des travaux des action méca qui agissent sur ce
système.
On n'as donc:
Wab(veteurP)+Wab(vecteurT)+Wab(vecteurR)=0
Déduire de cette égalité et des expréssion obtenues au 1 l'expression T pour
m=80kg;g=9.81m.s-2;alpha=30° et beta=45°
Centre d'inertie
le centre d'inertie d'un systeme constitué de 2 solides de masses m1, m2 et de centre d'inertie G1,G2 est le barycentre du
systeme ((G1,m1),(G2,m2))
J'ai essayer d'attacher une image mes mon image et tros grosse donc je vous passe ce lien voila :
** lien effacé **
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]() [lien]
[lien]
merci de ton aide pour l'image ! un peu d'aide silvoulait
Franchement rien c'est difficille je suis deçu depuis ce matin sa me prens la tete ^^
Question 1)
"Que peut-on dire du travail de la force vecRsol/ski?"
Quelle est son expression (applique la définition donnée dans l'énoncé)?
on peut dire quele vecteur Rsol/ski est perpendiculaire à la pente car on peut négliger les frottements du sol sur les skis.
et donc, pour le calcul du travail ?
Le travail de chacune des forces entre A et B est le produit scalaire du vecteur force par le vecteur AB: pour une force
par le vecteur F,Wab (vecteur F)=vecteurF.vecteurAB
Wab (vecteur R) = vecteur R * Vecteur AB ?? Peut etre sa je ne c'est pas
l'action de sol sur les skis (vecteur Rsol/ski, perpendiculaire à la pente, car on peut négliger les frottements
du sol sur les skis.
une propriété sur le produit scalaire quand 2 vecteurs sont orthogonaux, ça ne te dit rien ? -> cf. cours de maths
NON sa ne me dit rien on a pratiquemen rien fait sur le produit scalaire
donc je repon pour la question 1a) JE sais que l'action de sol sur les skis (vecteur Rsol/ski, perpendiculaire à la pente, car on peut négliger les frottements
du sol sur les skis.
OR DAPRés la propriété sur le produi scalaire quand deux vecteurs sont orthogonaux
On a Wab (vecteur R) = vecteur R * Vecteur AB
dacord merci ! sinon c'est bon ? On Peut passer a la suite ?
je ne c'est pas desoler !!! sa me soule 8h ke je suis dessu je suis nul en math
il faut que tu calcules le travail du poids en utilisant la formule donnée.
Normalement, tu as vu également cette formule EN COURS DE PHYSIQUE, à savoir
Wa->B(vecF) = vecF.vecAB = F.AB.sin(alpha) où alpha est l'angle entre les vecteurs vecF et vecAB
Il ne te reste plus qu'à l'appliquer ici.
Wa->B(vecR) = vecR.vecAB = R.AB.sin(ALPHA)???? je comprens rien
je t'ai donné la définition générale du cours
dans le cas de R, Alpha=90° donc sin(Alpha)=0 donc W(R)=0 on l'a dit tout à l'heure.
procède de même pour P
mais je comprens pa se que tu fait je les jamais fait en cours !! voila ce dm est pour lundi et personne peut m'aider cher moi jvé avoir une mauvaise note
je ne sais pas comment mieux l'expliquer.
si ton prof t'as donné ce DM, c'est que vous l'avez vu en cours, sinon c'est qu'il avait envie de mettre 0 à tout le monde...
Tu peux toujours regarder dans ton livre de physique tout seul, les formules et les méthodes y sont forcément !
j'ai deja regarder dans mon livre ce matin mais je ne comprens pas !! bref je compter sur vous !!
Je t'explique:
dans le cas général (je n'utilise pas ici les notations de ton exercice), pour calculer le travail d'une force sur un solide se déplacant de A vers B:
cela se lit "le travail de la force F entre A et B est égale à F scalaire AB".
Par définition, le produit scalaire se trouve en calculant le produit des normes et du cosinus de l'angle formé par les vecteurs F et AB (angle noté alpha):
il faut donc pour calculer le travail:
- la norme de la force (F)
- la distance parcourue (AB)
- l'angle entre les vecteurs F et AB (alpha)
merci sa m'eclaircie un peu !! donc pour calculer le travail : il me faut la norme de R  x²+y² 5 ( je ne sais pas combien fait x et y )
x²+y² 5 ( je ne sais pas combien fait x et y )
ensuite la distance entre a et b on la conné pas enfin je crois !
et l'angle entre R ET AB c 90Degres
Puis pour la question 1b) on calcul la norme de P  x²+y²(je ne sais pa combien fait x et y) ensuite la distance entre a et b on la sera grace a la question precedente et son angle on ne c'est pas on c juste que LE vecteur P soNT pois de norme p=mg, direction vertical par G .
x²+y²(je ne sais pa combien fait x et y) ensuite la distance entre a et b on la sera grace a la question precedente et son angle on ne c'est pas on c juste que LE vecteur P soNT pois de norme p=mg, direction vertical par G .
Merci de ton aide !! mais alors que vaut Le vecteur P ?? je ne vois pas
le vecteur P vaut sa norme multipliée par un vecteur de norme un qui en donne la direction et le sens !
 commme tu a s du le voir plu haut je n'est pratiquement pas fait de cour sur le produit scalaire jauré aimé que tu me detaille plus par ce que depuis ce matin je suis sur la 1ere question jessaye mais je n'y arrive pas voila
commme tu a s du le voir plu haut je n'est pratiquement pas fait de cour sur le produit scalaire jauré aimé que tu me detaille plus par ce que depuis ce matin je suis sur la 1ere question jessaye mais je n'y arrive pas voila 
Donc c'est seulement ça pour la question 1b) ? Puis pour la question 1a) la reponse est : je sais que l'action de sol sur les skis (vecteur Rsol/ski, perpendiculaire à la pente, car on peut négliger les frottements
du sol sur les skis.
Or DAPRés la propriété sur le produi scalaire quand deux vecteurs sont orthogonaux
On a Wab (vecteur R) = vecteur R * Vecteur AB
donc le travail est nul
Enfin  .Donc ensuite pour la 1c on sait que *L'action de la perche sur le skieur (vecteur Tperche/skieur), dont on notera T la norme, dont la direction suit
.Donc ensuite pour la 1c on sait que *L'action de la perche sur le skieur (vecteur Tperche/skieur), dont on notera T la norme, dont la direction suit
l'axe de la perche. ensuite je dois suremen utiliser une formule du produit scalaire et conclure que le produit scalaire et nul .

 !! sa peut faire ça non : vecT=T*AB*(cos(beta-alpha))
!! sa peut faire ça non : vecT=T*AB*(cos(beta-alpha))
