Inscription / Connexion Nouveau Sujet
Dm Volume maximum d'une boîte
Bonjour j'ai un dm en maths et il y a une question ou il me demande '' Fais un tableau donnant l'aire en fonction de x et le volume en fonction de x puis la représentation graphique de la mesure du volume en fonction de la mesure x du côté des carrés découpés c'est un carré qui mesure 20 cm. Je c'est pas quoi faire. Aidez moi svp??
bonjour,
des carrés découpés c'est un carré qui mesure 20 cm
des carrés (combien?) découpés (comment?)
donne toi la peine de recopier intégralement ton énoncé pour pouvoir avoir de l'aide!!
Bonjour,
c'est vrai que "recopier" ce n'est sans doute pas compréhensible, ce mot français...
on ne scane ni ne photographie ses énoncés
on les recopie
tu tapes avec ton clavier le texte de l'énoncé
et seule la figure a le droit d'être jointe (sans texte)
et si tu n'y arrives pas, décrite (exactement et complètement, tous les codages etc au besoin en rajoutant toi-même des noms de points)
je te conseille de lire (c'est obligatoire) le règlement du forum
le message "à lire avant de poster" (avant de poster)
et la FAQ (icones en haut du bandeau)
On dispose d'un carré, la mesure du côté est 20 cm. A chaque coin il est envisagé de découper un carré identique, la mesure de son côté x n'est pas déterminé. on obtient alors le patron d'une boîte sans couvercle. On veut déterminer la mesure de x du côté à découper pour que la mesure du volume de la boîte obtenue soit la plus grande possible.
Sa c'est l'énoncer.
(comprendre, ne pas comprendre, sait, c'est ... l'expression française est un truc de toute façon un peu flou pour Subsub27)
ah bein voila ...
il suffisait de mettre les points sur les i.
et juste après cet énoncé tu as la seule question : "Fais un tableau donnant l'aire en fonction de x et etc"
ou tu as des questions précédentes que tu as peut-être faites, et qu'as tu trouvé à ces questions précédentes ?
Oui j'avais 2 partie une partie tableur que je dois faire maintenant et une partie calcul que j'ai rendu.
Fais un tableau donnant l'aire en fonction de x et le volume en fonction de x puis la représentation graphique de la mesure du volume en fonction de la mesure x du côté des carrés découpés c'est un carré qui mesure 20 cm
et cela les questions?
le côté de la boîte est 20-2x--> A(fond de la boîte)=....................
la boîte est un pavé sans convercle--> V=surface de base*hauteur (hauteur=x)
J'ai pas trouvé car il faut le faire sur la tableur et je n'y arrive pas je suis nulle en informatique!
pour faire sur un tableur (ce qui n'est pas écrit)!!, il faut déjà avoir déterminé les expressions de l'aire et du volume en fonction de x
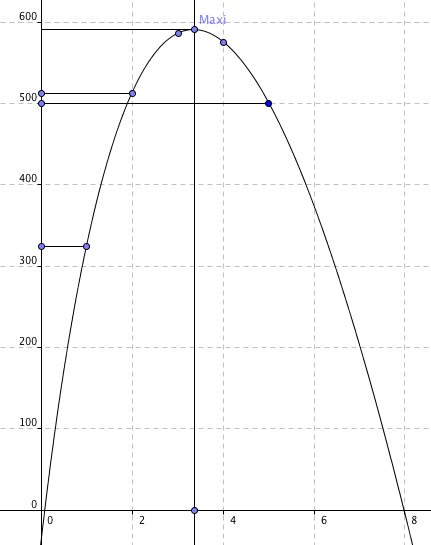
5-Estime à partir de la représentation graphique de la mesure du côté permettant d'obtenir une boîte dont la mesure du volume est maximum.
6-Fais la représentation graphique de la mesure de l'aire en fonction de la mesure x du côte des carrés découpés. y a-t-il proportionnalités?
volume de la boîte:
(20-2x)aucarréxX=x(20-2x)au carré
=(20aucarré-2(20x2X)+2xaucarré)X
=(20aucarré-40x2X+2Xaucarré)X
=(20aucarré-80x+2xaucarré)X
=(400-80x+2xaucarré)
=2xaucube-80Xaucarré+400X
(20-2x)aucarréxX=x(20-2x)au carré
=(20aucarré-2(20x2X)+2xaucarré)X
=(20aucarré-40x2X+2Xaucarré)X
=(20aucarré-80x+2xaucarré)X
=(400-80x+(2x)²)*x
=(400-80x+4x²)x
=4x^3-80x²+400x
Bonsoir à tous
Subsub27
Il y avait une partie calcul que le prof ma rendu il m'a dis c bon et une partie tableur.
par curiosité montre ce qui était bon, et ce n'est pas un tableur mais un tableau de valeurs en 2 lignes
la première avec des valeurs de x et la seconde avec les volumes correspondants en calculant
f(A)=4x3-80x2+400x
as-tu fait ce tableau ?
Bonjour mijo,
je doute de ce graphique ... pour une fonction V(x) = 4x^3 - 80x^2 + 400x
vu que pour x = 8 ça ne fait pas 0 !!
(un peu logique que ça ne soit pas 0 vu qu'aucune des dimensions de la boite ne vaut 0 pour x = 8 :
le fond à pour cotés 20 - 8 - 8 = 4 et la hauteur 8 donc le volume 4*4*8 = 128 !)
ça serait plutôt :
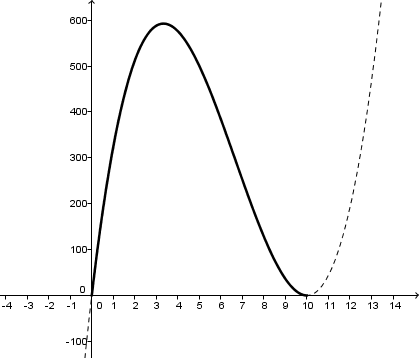
mais pour les questions incohérentes : énoncé à géométrie variable par petit bouts et dans le désordre, sans qu'on connaisse les résultats intermédiaires ni ce qui est vraiment attendu avec "un tableur"
alors qu'on a déja un tableau de valeurs paraît-il et que c'est exactement pareil.
.. moi j'ai jeté l'éponge depuis longtemps.
mais de là à donner des trucs faux ...
"le résultat" ?? aucune idée.
vu qu'on ne sait pas ce qu'on cherche vraiment
tantôt "un tableur", alors qu'on a déja un tableau mystère,
un tableur ne sert qu'à obtenir un tableau (de valeurs)
tantôt une question :
5-Estime à partir de la représentation graphique ...
mais :
1) c'est à toi de l'obtenir pour cette question là
soit à partir d'un tableau de valeurs (d'où le tableur ?) et les reporter sur du papier millimétré
soit directement avec ta calculette, ou avec un logiciel (ici j'ai utilisé Geogebra, mais on peut tout aussi bien utiliser Xcas ou Sinequanon etc)
2) et de chercher à utiliser ce graphique pour répondre aux questions demandées, quelles qu'elles soient.
Moi sur la fiche c'est écrit " Fais un tableau donnant l'aire en fonction de x et le volume en fonction de x puis la représentation graphique de la mesure du volume en fonction de la mesure x du côté des carrés découpés c'est un carré qui mesure 20 cm."
Il précise pas plus
c'est bien ce que je dis, un énoncé dont les questions changent d'heure en heure ... 
bein et le tableau tu l'as fait ou pas ??
et donc tu reportes les valeurs de ce tableau sur un graphique pour avoir la représentation graphique
et ça doit te donner quelque chose qui ressemble à la figure que j'ai donnée
et c'est tout pour cette question là du 17-02-16 à 00:34 (faut préciser la question horodatée à chaque fois ici, sinon on répond complètement à côté de la plaque)
Bonjour mathafou
Mon graphique mal fichu n'avait pour but que de montrer où se trouve approximativement le volume maxi cherché. Je pense qu'au niveau troisième, à partir du tableau, seul un encadrement de plus en plus serré des valeurs de x permet d'approcher au mieux la valeur maxi du volume