Inscription / Connexion Nouveau Sujet
Enigmo 113 : Gontran et Donald
Bonjour,
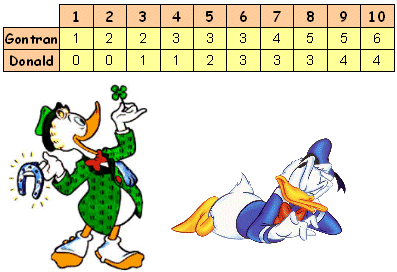
Gontran et Donald font une partie de "pile ou face" qui se déroule en 10 lancers. A chaque lancer, le gagnant marque 1 point.
Le tableau ci-dessous donne l'évolution du score des deux joueurs après chaque lancer au cours d'une partie : Gontran gagne 6 à 4 !
C'est bien connu, Gontran est un chanceux et ne perd jamais !
Ainsi, Gontran et Donald ont joué plusieurs parties, et Gontran n'a jamais été mené au cours d'une partie. Ils ont parfois été ex-aequo, en cours ou en fin de partie, mais à aucun moment Donald n'a mené.
Question : combien de parties (de 10 lancers) où Donald n'a jamais mené sont-elles possibles ?
Bonne recherche ! 
Bonjour,
sauf erreur Gontran le veinard peut gagner (ou au pire être ex-aequo avec Donald) sans être mené à aucun lancer, pour un ensemble de 252 parties...
Ici la tentation de faire un programme a été trop grande (plus sûr de ne pas oublier de cas et plus rapide aussi)!
Merci pour l'Enigmo.
Bonjour.
Il y a deux cent cinquante-deux (252) parties où Donald ne mène jamais.
Tableur pour un nombre pair de parties; autant de lignes et de colonnes plus une que de paires de parties
Première ligne : 1, 1, puis des 0
Formule en A2 : =A1+B1 à recopier dans le reste de la colonne.
Formule en B2 : = A1+C1+2*B1 à recopier dans le reste du tableau.
La case de colonne c et de rangée r indique le nombre de parties possibles de 2r lancers après lesquelles Gontran a une avance de 2*(c-1) points sans jamais été mené.
Gontran peut gagner 5 à 10 fois au cours d'une partie.
Pour une partie à 5 victoires, il y a (une combinaison de 5 parmi 10) parties possibles.
Pour une partie à 6 victoires, il y a (une combinaison de 6 parmi 10) parties possibles.
etc...
donc N = 10!/(5!5!) + 10!(6!4!) + 10!/(7!3!) ... + 10!/10!1!
N = 638
Bonsoir,
normalement, il existe 2^10 solutions ou Donald n'a jamais mené soit 1024 parties de 10 lancers
Bien à vous
Bonsoir
En suivant cette formule 
i=5 
10C10i je trouve 638 possibilités.
Voilà j'éspère ne pas être planté quelque part, et merci pour l'énigme
Bonjour,
je me suis trompé dans ma réponse.
Comme au premier lancer, il n'y a qu'une solution possible; la réponse est 2^9 solutions soit 512 parties où Donald n'a jamais mené !
J'ai donc donné l'ensemble des solutions pour tous les lancers (1024)
A bientôt
Je viens de m'apercevoir que je me suis planté, la formule que j'ai cité dans mon premier poste englobe toutes les possibilités dans les quels Gontran mène enfin de partie, mais j'ai pas filtré les possibilités dans les quels il perd au cour de la partie.
Je vais donc corriger ma réponse (par pure programmation) et dire 252 possibilités
Sur 1024 parties possibles (2 puissance 10), il y en a 252 pour lesquelles Donald ne mène jamais.
Merci pour l'énigme.
explication:
soit (i,j)un résultat de la n-ième partielle avec i
j et i+j=n
2 cas:
n est impair et j<i donc on multiplie par 2 chaque possibilité pour la (n+1)-ième partielle
n est pair et on peut avoir i=j et pour ce cas il n'y a qu'une possibilité au tour suivant
i+1,j)
donc on mutiplie par 2 et on retranche le nb de couples (i,i) pour avoir l'ensemble des résultats à la (n+1)-ième partielle
ce qui donne (je ne mets pas les ( ouvrantes et sachant qu'au premier coup on a forcément (1,0)
1*2*2-1)*2*2-2)*2*2-5)*2*2-14)*2=252
Bonjour
Le nombre de telles suites est 252
A comparer avec le nombre total de parties différentes :
On appelle J(n,d) le nombre de suites de n tirages qui donnent à Donald un gain de d
Alors le gain de Gontran est n-d
Si d<0 ou d>n-d, J(n,d)=0
De plus J(0,0)=1
Et pour finir, le nombre de suites de n tirages qui donnent le gain d est obtenu en partant des suites de n-1 tirages avec un gain d-1, où Donald gagne au tirage suivant
auxquelles on ajoute les suites de n-1 tirages avec un gain de d, où Gontran gagne au tirage suivant
J(n,d)=J(n-1,d-1)+J(n-1,d)
Le nombre de suites de longueur n où le gain de Donald est toujours à celui de Gontran est la somme sur d des J(n,d)
Je ne sais s'il existe pour J(n,d) ou pour sa somme une expression non récursive en n et d.
| d | ||||||||
| somme | 0 | 1 | 2 | 3 | 4 | 5 | ||
| 1 | n | 0 | 1 | |||||
| 1 | 1 | 1 | ||||||
| 2 | 2 | 1 | 1 | |||||
| 3 | 3 | 1 | 2 | |||||
| 6 | 4 | 1 | 3 | 2 | ||||
| 10 | 5 | 1 | 4 | 5 | ||||
| 20 | 6 | 1 | 5 | 9 | 5 | |||
| 35 | 7 | 1 | 6 | 14 | 14 | |||
| 70 | 8 | 1 | 7 | 20 | 28 | 14 | ||
| 126 | 9 | 1 | 8 | 27 | 48 | 42 | ||
| 252 | 10 | 1 | 9 | 35 | 75 | 90 | 42 |
Prochaine énigme : combien existe-t-il de parties différentes où Donald peut gagner un temps mais finit par perdre au bout des 10 lancés (ou être à égalité) face à son énervant cousin.
bonsoir jamo,
soit (x,y) le couple d'entiers naturels représentant les scores de Gontran et Donald,les couples possibles en fin de partie sont
(10,0),(9,1),(8,2),(7,3),(6,4),(5,5)
Donald ne menant jamais à l'issue de chaque lancer on a xy et le point M(x,y)est strictement sous la droite d'équation y=x+1
j'ai donc cherché le nombre de chemins monotones croissants joignant l'origine aux six terminaux possibles et ne traversant pas la droite d'équation y=x
je trouve
ce qui donne 252 possibilités
il y a donc sauf erreur dans mes calculs 252 parties possibles
merci pour cet intéressant énigmo.
Bonjour !
Voici ma réponse :
Il y a 252 parties possibles (de 10 lancers) où Donald n'a jamais mené.
Je n'ai pas le courage de faire de la théorie pour justifier ce résultat. Par contre cela m'interesserait de la connaître. Je peux simplement dire qu'il y a parties de 10 lancers possibles. Grâce à Maple je les ai simulé et compté qu'il y a en a 252 qui vérifient la condition du problème.
Merci !
Les probabilités pour Donald de gagner vont de 0/10 à 5/10 ce qui en séquence de 10 coups donne :
(Avec 0=gagné et 1 = perdu)--->0000000000 à 0101010101.
Je me réfère donc au mode binaire
Jamais Donald ne gagnera le premier coup d'une partie .
En binaire nous aurions 2 puissance 9 cas soit 512 parties mais on sait qu'en cumul jamais Donald ne sera devant Gontran par exemple la séquence pour Donald 0000111110 est impossible de même toutes les séquences supérieures à 0101010101
je trouve 90 séquences du premier type et 170 du second .
Donc 512-90-170 =maximum 252 parties
252 parties :
1 avec le score de 10 à 0
9 avec le score de 9 à 1
35 avec le score de 8 à 2
75 avec le score de 7 à 3
90 avec le score de 6 à 4
42 avec le score de 5 à 5
Je propose 252 parties sur 1024 possibles.
public class Main {
static private int wins = 0;
public static void main(String[] args) {
boolean[] plies = new boolean[10];
perform(plies);
}
private static void perform(boolean[] plies) {
plies[0] = true;
perform(plies, 1);
}
private static void perform(boolean[] plies, int index) {
if (index > plies.length - 1) {
wins++;
System.out.print("" + wins + ") ");
for (int i=0 ; i<plies.length ; i++) {
if (plies[i]) {
System.out.print("1");
} else {
System.out.print("0");
}
}
System.out.println("");
return;
}
int count = 0;
for (int i=0 ; i<index ; i++) {
if (plies[i]) {
count ++;
}
}
if (2*count < index) return;
plies[index] = false;
perform(plies, index + 1);
plies[index] = true;
perform(plies, index + 1);
}
}
Bonjour
-----Réponse proposée-----
Il existe 252 parties (de 10 lancers) où Donald n'a jamais mené
-----Méthode employée-----
Elaboration de l'arbre des scores à partir de la 10eme partie(10-0, 9-1, 8-2, 7-3, 6-4, 5-5), en remontant vers la première (1-0)
Il suffit alors, à chaque niveau, de faire la somme des branches et de remonter ainsi à la première partie pour que la somme soit égale à 252.
Pour éviter de trouver cette solution "à la main", il aurait été souhaitable de demander un plus grand nombre de lancers, par exemple 20 lancers => 184 756 parties, ou 100 lancers => 100 891 344 545 564 000 000 000 000 000 parties
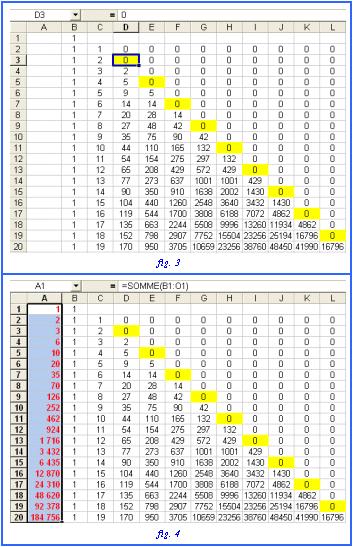
-----Méthode excel-----
On peut, en quatre images, présenter la procédure d'utilisation d'excel
fig.1 : mettre des 1 dans les cellules de la colonne B : [By = 1]
fig.2 : dans la cellule C2, faire la somme des 2 cellules B1 et C1 [C2=B1+C1]; puis étendre cette formule dans le reste du tableau : on crée ainsi le triangle de Jia Xian (XIe siècle), repris par Tartaglia puis Pascal (XVIIe siècle)
fig.3 : forcer à zéro les cellules D3, E5, F7... colorées en jaune [D3=1]
fig.4 : il ne reste plus qu'à faire les sommes lignes par lignes avec le résultat dans la colonne A [A1=SOMME(B1,Z1)]
La ligne N=10 fournit la valeur A10=252
-----Enigme dérivée-----
On peut aussi contraindre les deux joueurs à ne jamais être ex-aequo
Rudy
Bonjour ^^
Moi j'ai trouvé 6 parties possibles :
Gontran : 10/ Donald : 0 ;
Gontran : 9 / Donald : 1 ;
Gontran : 8 / Donald : 2 ;
Gontran : 7 / Donald : 3 ;
Gontran : 6 / Donald : 4 ;
Gontran : 5 / Donald 5 .
Voilà ^^ j'espère que c'est ça
Avec un petit bruteforce (oui petit, sur 1024 cas...), je trouve 252 solutions.
Merci pour cette sympatique énigme.
bonjour,
j'ai pu trouver la solution à l'aide du compilateur "Pascal" (dépassé je sais 
) ...
donc ma réponse est 353 parties possibles...
Salut jamo,
je trouve au total 198 parties possibles au cours desquelles Donald n'a jamais mené, en espérant ne pas en avoir oublié une ou deux au passage
Encore merci pour l'énigme !
Voila, donc j'ai cherché toutes les solutions et j'ai trouvé 2*3*3*3*3 = 162 possibilités !!
Ci joint un tableau des possibilités, 1 representant Gontran gagne cette manche et rien Gontran la perds
Clôture de l'énigme
La bonne solution est : 252 parties.
Pour les explications, je vous invite à lire celles détaillées ci-dessus qui utilisent des tableaux, je pense que c'est ce qu'il y a de plus simple.
mon programme a l'air de marcher bien dans le début mais il lui arrive quoiiiii ???!!!!!!!!! 353 au lieu de 252 rrrrrrrrrrr.....
Bonjour,
C'est une énigme très intéressante; le résultat dans le cas général (pour une partie en n lancers) est : ; on a bien
.
Il y a une démonstration très courte en interprétant par des chemins croissants suivant les lignes d'un quadrillage et en utilisant le lemme suivant:
Le nombre de chemins croissants allant de O(0,0) au point A(p,q) et ne traversant pas la droite (y=x) est égal à .
Le nombre de chemins de longueur n partant de O et ne traversant pas la droite (y=x) est alors égal à puisque un tel chemin se termine en A(n-k,k) avec
.
La démonstration du lemme est très astucieuse et utilise le principe de Désiré André. Le nombre total de chemins croissants allant de O à A(p,q) est égal à . A un chemin partant de O et traversant la droite (y=x) on associe bijectivement un chemin partant du point O'(-1,1) en symétrisant par rapport à la droite (y=x+1) la partie du chemin joignant O au premier point sur la droite (y=x+1). Comme il y a
chemins de 0' à A(p,q) on a bien le résultat annoncé.
Une remarque pour Rudi: pour n=100 on obtient (il faut calculer avec 32 chiffres significatifs!)
Bonjour,
Il y a bien 252 "évolutions des scores" possibles, qui correspondent à 1024×252 = 258 048 parties différentes, selon le résultat des lancés.
Je me disais bien que je n'avais pas tout compris ...
"Why simple when something difficult's possible?" 
Nombre de participations : 0
0,00 %0,00 %
0Temps de réponse moyen : 101:36:30.
Annuler
connectez vous