Inscription / Connexion Nouveau Sujet
Enigmo 291 : Soyons fous !
Bonjour tout le monde,
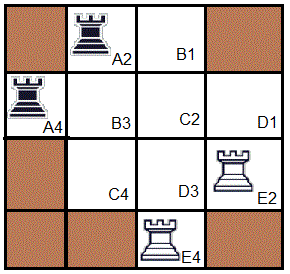
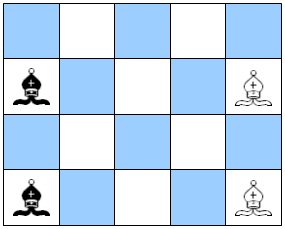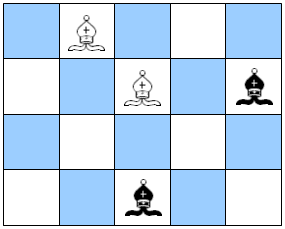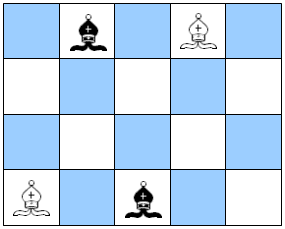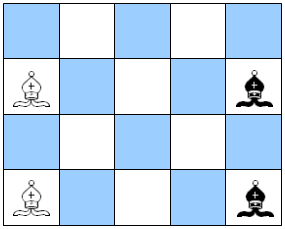
deux fous blancs et deux fous noirs sont sur un petit échiquier, initialement dans la position indiquée par l'image ci-dessous.
L'objectif est d'intervertir les fous blancs et les fous noirs, en respectant les règles suivantes :
- les fous peuvent se déplacer selon la règle aux échecs, c'est-à-dire en diagonale, d'autant de cases qu'il est possible ;
- deux fous de couleurs différentes ne peuvent pas se trouver en prise (donc pas sur une même diagonale).
Bien entendu, l'objectif est d'intervertir les fous avec le minimum de coups.
Question : Donner la plus petite liste possible des mouvements des fous afin d'intervertir les blancs et les noirs.
Pour la réponse, vous donnerez tous d'abord le nombre de coups, puis la liste des coups selon le modèle suivant :
1 : A2 B3
2 : E4 B1
3 : E2 D3
...
Et si vous pensez que le problème est impossible, vous répondrez "problème impossible".
Bonne recherche ! 
 Je pense que si le problème était possible, on aurait pu le trouver plus rapidement...
Je pense que si le problème était possible, on aurait pu le trouver plus rapidement...
J'arrive facilement à en positionner 3 sur 4 .. mais jamais le dernier.
C'est pourquoi, je dirais sans en être certain, que le problème est impossible.
 Bonjour
Bonjour
Normalement les fous sont sur une diagonale noire et une blanche
Dans cette énigme si les blancs et les noirs doivent être bougés
alternativement ,je ne vois pas de solution.
 sans conviction 20 coups
sans conviction 20 coups
1 a2-b3
2 e2-d3
3 b3-d1
4 d3-b1
5 a4-b3
6 d1-e2
7 b3-c4
8 b1-c2
9 c2-a3
10 c4-a2
11 e2-c4
12 e4-c2
13 c2-d1
14 c4-d3
15 a2-b1
16 d3-e4
17 d1-b3
18 b1-d3
19 d3-e4
20 b3-a2
j'espere ne pas avoir fait d'erreur...
 Bonsoir,
Bonsoir,
pas mieux que 18 coups (malgré mes espoirs parfois).
Il y a plusieurs variantes à 18 coups; en voici une :
01: e2-d3
02: a4-d1
03: a2-b3
04: d3-b1
05: d1-e2
06: b3-c4
07: e4-c2
08: c2-a4
09: b1-c2
10: c4-a2
11: e2-c4
12: c2-d1
13: a2-b1
14: b1-e4
15: c4-d3
16: d1-b3
17: b3-a2
18: d3-e2
Merci, jamo, pour ce problème très sympa.
(les deux étoiles réconfortent quant à la solution en 18 coups (minimale sauf erreur))
PS: Si j'ai le temps, que la solution fait bien 18 coups et que personne n'aura eu l'idée, je posterais la réponse en animation.
 Bonjour,
Bonjour,
le nombre de coups : 18 coups
la liste des coups :
1: A2 B3
2: E4 B1
3: E2 D3
4: B3 D1
5: B1 A2
6: D3 C4
7: D1 C2
8: C4 E2
9: A2 C4
10: C2 B1
11: A4 C2
12: C2 E4
13: C4 B3
14: E2 D1
15: B1 D3
16: B3 A2
17: D1 A4
18: D3 E2
Merci pour cette énigme !
 Bonjour,
Bonjour,
Encore un problème amusant à résoudre. Thanks !
18 mouvements à réaliser.
01: A2 B3
02: E2 D3
03: B3 D1
04: D3 C4
05: E4 B1
06: B1 A2
07: D1 C2
08: C2 E4
09: A4 C2
10: C4 E2
11: A2 C4
12: C2 B1
13: E2 D1
14: D1 A4
15: C4 B3
16: B1 D3
17: B3 A2
18: D3 E2
 Bonjour,
Bonjour,
18 coups
1:A2-B3
2:E4-B1
3:E2-D3
4:B3-D1
5:B1-A2
6 3-C4
3-C4
7 1-C2
1-C2
8:C4-E2
9:C2-E4
10:A4-C2
11:A2-C4
12:C2-B1
13:E2-D1
14 1-A4
1-A4
15:C4-B3
16:B1-D3
17:B3-A2
18 3-E2
3-E2
 Bonjour,
Bonjour,
Il y a des smileys qui sont apparus de façon inopportune dans ma réponse pour une raison que j'ignore.
Il convient de lire 6 3-D4 7: D1-C2 14
3-D4 7: D1-C2 14 1-A4 18: D3-E2
1-A4 18: D3-E2
 Bonjour,
Bonjour,
J'y perds mon latin. Je viens de réaliser que les signes: et D accolés sans espace blanc donnent un smiley!!!!
Les smileys de ma solution sont donc à remplacer par : D
 bonjour !
bonjour !
Je sais que ça sent très fort le poisson, mais je n'ai pas trouvé moins que 18 déplacements :
A2 B3
E2 D3
B3 D1
D3 C4
E4 B1
B1 A2
D1 C2
C4 E2
A2 C4
C2 B1
A4 C2
C2 E4
E2 D1
D1 A4
C4 B3
B1 D3
D3 E2
B3 A2
Je vous inviterai pour une bonne bouillabaisse 
Kidamicalement
 Bonjour et merci à Jamo
Bonjour et merci à Jamo
"Intervertir les fous blancs": Si je comprends bien , il faut permuter le blanc du haut et celui du bas? (on pourrait comprendre autrement, les blancs remplaçant les noirs..mais alors quel fou blanc pour quel fou noir? il manquerait une indication là-dessus)
"Autant de cases qu'il est possible": la position du copain fou est un obstacle infranchissable?
Avec ces règles du jeu, je trouve une solution en 10 coups:
1: A2-B3
2: E4-B1
3: E2-D3
4: B3-A2
5: A4-B3
6: D3-E4
7: B1-D3
8: B3-A2
9: D1-A4
10: D3-E2
 Bonsoir Jamo,
Bonsoir Jamo,
"problème impossible"
après avoir parcouru 2175 chemins impossibles (impasse)
ayant au maximum 23 coups.
Merci pour la recherche.
 Bonjour
Bonjour
Il semblerait qu'il n'y a pas de solution
( alors qu'à 1ère vue on aurait pensé le contraire )
A+
 Bonjour à tous.
Bonjour à tous.
Ma réponse : 18 coups
1:A2 B3
2:E2 D3
3:B3 D1
4 3 C4
3 C4
5:E4 B1
6:B1 A2
7 1 C2
1 C2
8:C2 E4
9:A4 C2
10:C4 E2
11:A2 C4
12:C2 B1
13:E2 D1
14 1 A4
1 A4
15:C4 B3
16:B1 D3
17 3 E2
3 E2
18:B3 A2
Merci pour l'énigme.
 Je reposte en raison des smileys intempestifs qui se sont glissés dans ma réponse
Je reposte en raison des smileys intempestifs qui se sont glissés dans ma réponse
Ma réponse : 18 coups
1: A2 B3
2: E2 D3
3: B3 D1
4: D3 C4
5: E4 B1
6: B1 A2
7: D1 C2
8: C2 E4
9: A4 C2
10: C4 E2
11: A2 C4
12: C2 B1
13: E2 D1
14: D1 A4
15: C4 B3
16: B1 D3
17: D3 E2
18: B3 A2
 Bonjour,
Bonjour,
problème impossible.
Je n'ai pas trouvé d'explication qui soit très claire, mais je suis persuadé qu'elle sera donnée.
Pour information, aux échecs féeriques, cette condition s'appelle Échecs Isardam.
Les problèmes sur échiquiers réduits existent également, mais on y conserve la notation classique dans laquelle la case A1 est toujours située en bas à gauche.
Mais ceci est dit en toute amitié.
Merci pour l'énigme.
 Bonjour,
Bonjour,
Je propose une solution en 8 coups :
1: A4-D1
2: E4-C2
3: E2-C4
4: D1-E2
5: C2-A4
6: A2-B1
7: C4-A2
8: B1-E4
Bon dimanche !
 21 coups :
21 coups :
Mouvement 1: a2-b3
Mouvement 2: e2-d3
Mouvement 3: d3-b1
Mouvement 4: b3-d1
Mouvement 5: e4-d3
Mouvement 6: d3-c4
Mouvement 7: b1-a2
Mouvement 8: d1-c2
Mouvement 9: c2-e4
Mouvement 10: c4-e2
Mouvement 11: a2-c4
Mouvement 12: e4-b1
Mouvement 13: a4-c2
Mouvement 14: c2-e4
Mouvement 15: e2-d1
Mouvement 16: c4-b3
Mouvement 17: b3-a4
Mouvement 18: b1-d3
Mouvement 19: d1-b3
Mouvement 20: b3-a2
Mouvement 21: d3-e2
A+
Torio
 Bonjcur,
Bonjcur,
Je trouve 18 déplacements. Les voici :
1 : A2 B3
2 : E4 B1
3 : E2 D3
4 : B3 D1
5 : B1 A2
6 : D3 C4
7 : A4 C2
8 : C2 E4
9 : D1 C2
10 : C4 E2
11 : A2 C4
12 : C2 B1
13 : E2 D1
14 : C4 B3
15 : B1 D3
16 : B3 A2
17 : D1 A4
18 : D3 E2
Merci pour l'énigme. 
 Si l'on impose de bouger alternativement un fou blanc et un fou noir (comme il serait normal au jeu d'échec), alors le problème est impossible. En autorisant de bouger plusieurs fois de suite des fous de même couleur, on peut faire en 11 coups (peut-être moins ?).
Si l'on impose de bouger alternativement un fou blanc et un fou noir (comme il serait normal au jeu d'échec), alors le problème est impossible. En autorisant de bouger plusieurs fois de suite des fous de même couleur, on peut faire en 11 coups (peut-être moins ?).
 Bonjour
Bonjour
Voici ma proposition en 18 mouvements.
Elle commence par les trois mêmes mouvements que ceux proposés dans l'énoncé.
1 : A2 B3
2 : E4 B1
3 : E2 D3
4 : B3 D1
5 : B1 A2
6 : D3 C4
7 : D1 C2
8 : C4 E2
9 : A2 C4
10 : C2 E4
11 : A4 C2
12 : C2 B1
13 : C4 B3
14 : E2 D1
15 : B1 D3
16 : B3 A2
17 : D1 A4
18 : D3 E2
c'est extrêmement subjectif, je sais, mais personnellement j'aurais accordé plus de deux étoiles à ce problème.
merci beaucoup pour cet enigmo, et à bientôt
 Bonjour,
Bonjour,
Je n'ai pas trouvé de solution, donc je réponds :
problème impossible
même si je n'ai pas trouvé pourquoi c'était impossible ... et ça ne l'est donc peut-être pas ...
 Bonjour sans problème de croisement de pièce il faut au 2 coups pour déplacer chacun des 4 fous.
Bonjour sans problème de croisement de pièce il faut au 2 coups pour déplacer chacun des 4 fous.
malgré les problemes de croisement, la solution en 8 coups
1:E4-B1
2: E2-D1
3: A2-C4
4: C4-E2
5: A4-C2
6: C2-E4
7: B1-A2
8: D1-A4
arrive au résultat souhaité donc il me semble impossible de faire moins!
 Salut jamo,
Salut jamo,
Je propose 18 coups :
1 : A2 B3
2 : E4 B1
3 : E2 D3
4 : B3 D1
5 : B1 A2
6 : D3 C4
7 : A4 C2
8 : C2 E4
9 : D1 C2
10 : C4 E2
11 : A2 C4
12 : C2 B1
13 : E2 D1
14 : D1 A4
15 : C4 B3
16 : B1 D3
17 : B3 A2
18 : D3 E2
Merci.
 Bonjour,
Bonjour,
En 8 coups je propose :
1: A2 B1
2: A4 D1
3: E4 C2
4: C2 A4
5: E2 C4
6: C4 A2
7: B1 E4
8: D1 E2
 18 coups
18 coups
E2 D3
A2 B3
D3 B1
B3 C4
A4 D1
D1 E2
E4 C2
C2 A4
B1 C2
C4 A2
E2 C4
C2 D1
C4 D3
A2 B1
D1 B3
D3 E2
B1 E4
B3 A2
Merci Jamo
 J'ai compté (pas à la main
J'ai compté (pas à la main  ) 2304 variantes à 18 coups (bon courage pour la correction)
) 2304 variantes à 18 coups (bon courage pour la correction)
A2 B3 ; E4 B1 ; E2 D3 ; B3 D1 ; D3 C4 ; B1 A2 ; D1 C2 ; C2 E4 ; A4 C2 ; C4 E2 ; A2 C4 ; C2 B1 ; E2 D1 ; D1 A4 ; C4 B3 ; B1 D3 ; D3 E2 ; B3 A2
...
Bravo à ceux qui ont fait l'énigme à la main et encore:
merci Jamo
Clôture de l'énigme
Voilà une énigme qui n'était finalement pas si facile !
Même si le principe était simple à comprendre (d'où les 2 étoiles pour la difficulté), trouver une solution n'était pas évident, et être certain qu'elle était minimale encore moins.
Bravo à ceux qui ont trouvé ! 
 Bravo à ceux qui ont trouvé
Bravo à ceux qui ont trouvé  .
.
J'aurais du insister plus...
En revanche, je conteste totalement la validité de la réponse de pdiophante qui a clairement abusé des  .
.
 Je ne trouve plus mes 11 coups, que j'ai sûrement révés !
Je ne trouve plus mes 11 coups, que j'ai sûrement révés ! 
Sans doute que beaucoup de participants ont essayé de bouger alternativement blancs et noirs, suivant l'habitude des échecs ? Auquel cas le problème est effectivement impossible
 Bonsoir,
Bonsoir,
chose promise, chose due !
NB: Le gif correspond à la solution que j'ai donné initialement, mais il en existe d'autres...
 Et un poisson bien mérité pour Alishisap qui n'a pas cherché plus loin que le bout de son nez, un !
Et un poisson bien mérité pour Alishisap qui n'a pas cherché plus loin que le bout de son nez, un !
Quoique ça m'étonnerais franchement que je sois parvenu à trouver une solution (et encore plus de trouver la meilleure) même si j'avais cherché plus longtemps étant donné la complexité de celle-ci.
J'étais dans le même cas que Nofutur : impossible de placer ce fichu dernier fou.
Je félicite chaudement tous ceux et celles qui ont résolu l'énigme !
PROMIS, j'y réfléchirais à deux fois à partir de maintenant avant de mettre "problème impossible".
 Bonsoir à tous!
Bonsoir à tous!
Avant de poster ma réponse , j'avais donné mon interprétation de l'énoncé, que je trouvais peu clair.
Il me semblerait opportun que Jamo précise un peu..
 Jolie animation, merci Manpower.
Jolie animation, merci Manpower.
Sans doute que beaucoup de participants ont essayé de bouger alternativement blancs et noirs, suivant l'habitude des échecs ?
Oui, et merci Jamo car son exemple levait le doute :
1 : A2 B3
2 : E4 B1
3 : E2 D3
Pour limiter le nombre branches à explorer (moins de 36000), mon programme mémorise le nombre de coups minimum pour toutes les positions rencontrés (100) et limite ainsi la recherche aux chemins les plus courts. Cela permet une exploration complète de l'arbre avec au final 2304 (28*32) variantes à 18 coups.
 Alishisap:
Alishisap:
Oui, mais j'utilise Xcas: ![]() [lien]
[lien]
Et comme je ne suis pas fier de ma programmation (trop confus), je préfère l'envoyer par mail, voir mon profil pour m'envoyer une adresse mail.
 Toujours pas de réponse à ma question:
Toujours pas de réponse à ma question:
Intervertir les fous blancs et les fous noirs peut signifier:
*intervertir les fous blancs et intervertir les fous noirs
*intervertir chaque fou blanc avec un fou noir, mais alors comment choisir ce fou noir parmi les deux?
J'ai donc penché pour la première interprétation.
 Salut Rogerd,
Salut Rogerd,
Pour moi, il n'y avait pas d'ambiguïté dans la question.
Et de toute façon, ta réponse (quelle que soit ton interprétation) ne respecte par cette règle :
deux fous de couleurs différentes ne peuvent pas se trouver en prise (donc pas sur une même diagonale)
 Merci Kidam pour la vérification de ma solution.
Merci Kidam pour la vérification de ma solution.
Il y a bien une faute: deux fous de couleur différente en B1 et A2.
Mea culpa.
 Bonjour,
Bonjour,
il faudrait vraiment que je lise les sujets autrement qu'en diagonale....j'ai zappé la deuxième règle....(sans celle la c'était vraiment facile....).
c'est rageant!
Nombre de participations : 0
Temps de réponse moyen : 138:26:17.