Inscription / Connexion Nouveau Sujet
Enigmo 297 : Les triangles raisonnables
Bonjour tout le monde,
nous appellerons "triangle raisonnable" un triangle dont les trois angles sont en progression arithmétique, et dont les longueurs des côtés sont en progression géométrique.
Pourquoi raisonnable ? Je vous laisse deviner ... 
Question : Trouver tous les triangles raisonnables.
Si vous pensez qu'il n'en existe pas, vous répondrez "problème impossible".
Si vous pensez qu'il en existe un ou plusieurs, il faudra pour chacun d'entre eux me donner les valeurs de ses angles et les longueurs de ses côtés.
Et s'il en existe plusieurs, il faudra bien tous les donner, d'une manière ou d'une autre !
Un triangle dont les longueurs des côtés sont nulles ne sera bien entendu pas accepté.
Bonne recherche ! 

 Une première remarque .. Si un triangle est solution, tous les triangles semblables à cette solution sont également solutions.
Une première remarque .. Si un triangle est solution, tous les triangles semblables à cette solution sont également solutions.
Si on considère uniquement la forme du triangle, je ne trouve qu'une solution qui est le triangle équilatéral.
Trois côtés égaux (raison égale à 1), valeur quelconque a.
Trois angles égaux (raison égale à 0), valeur égale à 60°.
 les angles sont en progressions arithmetiques donc
les angles sont en progressions arithmetiques donc
A<=B<=C et B =60 et C<120
donc sin A <= sin B <= sin C
et b*b=a*a+c*c-a*c
a/sin a = b/sin b = c/sin c donc
a <= b <= c
donc b*b = a*c
(a-c)2 = 0
donc a=c( et donc = b)
 Bonjour,
Bonjour,
Les triangles raisonnables sont les triangles équilatéraux.
Ce sont donc les triangles ABC avec
angle(A) = angle(B) = angle(C) = 60 degrés
et
AB = BC = CA = a
où a est un réel strictement positif donné.
Chaque valeur de a donne donc une solution.
Merci pour cette énigme, on regrette qu'il n'y ait pas d'autres solutions !
 Bonjour
Bonjour
Tout d'abord, une réponse triviale:
avec une suite arithmétique de raison nulle (donc suite constante), et une suite géométrique de raison unitaire (donc également suite constante), on obtient que tout triangle équilatéral est raisonnable.
Mais est-ce tout? peut-être pas...
Pour le vérifier, on doit écrire la progression arithmétique de raison pour les angles:
(où la valeur de se déduit directement de la contrainte sum la somme des angles du triangle),
puis la progression géométrique de raison k des côtés:
.
A la suite de quoi, il suffit d'écrire le théorème de Pythagore généralisé sur l'angle pour obtenir :
qui se réduit à , équation indépendante de b qui n'a de solution que pour k=1.
Si la seule solution est k=1, alors les seuls triangles raisonnables sont les triangles équilatéraux.
Puisqu'il faut en donner la valeur des angles et des longueurs de côté, ce sera donc: 60° pour chaque angle, et des longueurs (a=b=c) identiques strictement positives pour les trois côtés.
Merci pour cet énigmo !
 Bonjour à tous.
Bonjour à tous.
Sauf erreur de ma part, le seul triangle "raisonnable" est le triangle équilatéral : 3 anges de 60 degrés
(progression arithmétique de raison 0) et les 3 côtés ont la même longueur (progression géométrique de raison 1).
Merci pour l'énigme.
 Les triangles raisonnables sont TOUS les triangles équilatéraux
Les triangles raisonnables sont TOUS les triangles équilatéraux
( 3 angles à 60° et des côtés de longueur x)
Il y en a donc une infinité, mais TOUS sont équilatéraux.
La progression arithmétique est de raison 0
La progression géométrique est de raison 1
 Les triangles raisonnables sont exactement les triangles équilatéraux, et rien qu'eux.
Les triangles raisonnables sont exactement les triangles équilatéraux, et rien qu'eux.
Les angles d'un triangle raisonnable sont avec
. Si on range les sinus dans l'ordre croissant on trouve
où
et
.
Les côtés d'un triangle raisonnable dans l'ordre croissant sont avec
(plus d'autres inégalités conséquences de l'inégalité triangulaire).
La loi des sinus nous donne les équations et
. En multipliant terme à terme on obtient
, d'où
ce qui ne laisse comme possibilité que
.
 Bonjour Jamo,
Bonjour Jamo,
Tout triangle est raisonnable ssi il est équilatéral de longueur de côté non nulle.
Il est visiblement équilatéral, ton triangle de Legoland (Dk)
Merci pour l'énigmo.
 Le triangle équilatéral
Le triangle équilatéral
angle : 60° 60° 60° trois angles en progression arithmétique de raison nulle (r=0)
de coté a a a (a>0 a
 *) les longueurs des côtés sont en progression géométrique de raison 1 (q=1)
*) les longueurs des côtés sont en progression géométrique de raison 1 (q=1)
Il n'y pas d'autre solution.
Mais comme il n'y a pas de « progression » cette solution est limite, j'aurais pu répondre problème impossible.
bonjour et merci Jamo
 Bonjour
Bonjour
Tout triangle équilatéral convient est un triangle raisonnable
car
Les angles : A= B-r ; B ; C= B+r => B=pi/3 ; les côtés : a ; aq ; aq²
relation aux sinus
a/sin(B-r) = b/sin(B) = c/sin(B+r) => a/sin(pi/3-r) = 2aq/V3 = aq²/sin(pi/3+r)
=>
2.q.sin(pi/3-r) = V3 et 2.sin(pi/3+r) = V3.q
En multipliant on a
4sin(pi/3-r).sin(pi/3+r) = 3
=> cos(2.r) - cos(2pi/3) = 3/2
=> cos(2r) + 1/2 =3/2
=> cos(2r) = 1
=> r =0 (triangle équilatéral )
Et alors a=b=c et q =1
Toute suite constante est une suite géométrique de raison 1 =>
Tout triangle équilatéral est raisonnable
A+
 Bonjour,
Bonjour,
Seuls les triangles équilatéraux sont raisonnables.
Et pourquoi donc ?
On peut montrer que les angles sont 60 - x, 60, 60 + x.
On peut aussi décider que un des côtés de l'angle de 60° vaut 1.
Dans ces conditions, on peut distinguer deux cas:
Cas n°1 : B< (B²+1-B)<1
(B²+1-B)<1
 (B²+1-B)=rB
(B²+1-B)=rB
1=r²B
verifié uniquement si B=1
Cas n°2 : B>1
 (B²+1-B)=r
(B²+1-B)=r
B=r²
verifié uniquement si B=1
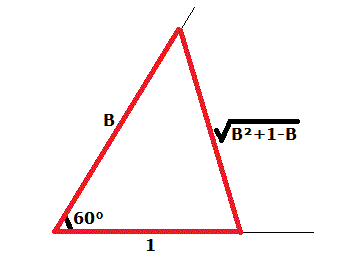
 Je disais ci-dessus que "Seuls les triangles équilatéraux sont raisonnables."
Je disais ci-dessus que "Seuls les triangles équilatéraux sont raisonnables."
En relisant l'enoncé, je ne suis pas sûr que cette formulation réponde précisement à la question posée:
"Si vous pensez qu'il en existe un ou plusieurs, il faudra pour chacun d'entre eux me donner les valeurs de ses angles et les longueurs de ses côtés. Et s'il en existe plusieurs, il faudra bien tous les donner, d'une manière ou d'une autre !".
Bien sûr, on peut aussi donner comme réponse : Un triangle est raisonnable si et seulement si ses trois angles sont égaux à 60°
Merci pour cette énigme !
 Bonjour !
Bonjour !
C'est évidemment le théorème d'Al-Kashi qui fixe les rapports angles/longueurs dans un triangle.
On écrit donc les trois relations et le fait que la somme des angles fait 180 degrés d'où 4 équations à 4 inconnues (les deux raisons et les deux premiers termes) d'où le système que Maple a résolu a ma place (par fainéantise, car à la main, il se fait bien) et j'obtiens que la seule solution possible est tous les triangles équilatéraux.
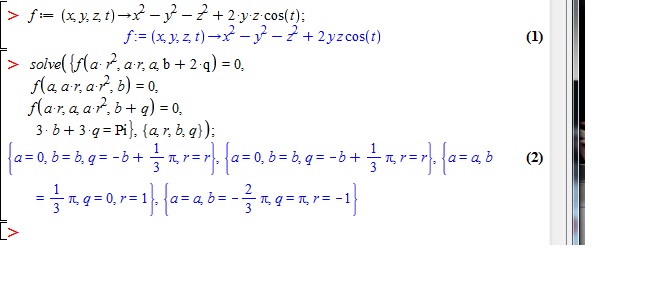
 Bonjour Jamo,
Bonjour Jamo,
L'énoncé n'interdisant pas les progressions arithmétiques de raison nulle, ni les progressions géométriques de raison unité, il y a une infinité de solutions, à savoir tous les triangles équilatéraux (et seulement eux). Ils se caractérisent , comme chacun sait, par :
- trois angles égaux à  /3
/3
- trois côtés égaux entre eux, de longueur a  ]0,+
]0,+ [
[
 Bonjour, Jamo! Bonjour, tous!
Bonjour, Jamo! Bonjour, tous!
Je propose comme solution...
les triangles équilatéraux, soient (60°, 60°, 60°) pour les angles et (a, a, a) pour les côtés (a réel, a>0).
On serait tenté de dire "problème impossible", mais j'ose croire que rien n'interdit qu'une progression arithmétique ait comme raison 0 et une progression géométrique 1!
Merci pour l'énigmo!
 Bonjour,
Bonjour,
après n'avoir trouvé nulle part pourquoi une progression arithmétique (ou géométrique) ne pourrait pas être constante, je dirais que la seule façon d'obtenir ce que l'on souhaite est pour des angles et des côtés égaux.
Le triangle équilatéral est l'unique triangle raisonnable! (donc angles égaux à 60 tous les trois et côtés de dimension quelconque, mais identique pour les trois).
Mon mois de réponses expresses à pris fin.... pour des raisons franchement indépendantes de ma volonté (personne ne sait comment revenir en arrière dans le temps? si oui ca m'intéresse...)
pour des raisons franchement indépendantes de ma volonté (personne ne sait comment revenir en arrière dans le temps? si oui ca m'intéresse...)
 Bonjour,
Bonjour,
J'ai pris une nuit de réflexion:
1/pour la progression des angles cela implique
que l'angle médian fasse 60°.
2/pour la progression géométrique des cotés cela implique
que les deux autres fassent aussi 60 ° (triangle équilatéral)
Donc les deux progressions seraient nulles.
 Bonjour à tous,
Bonjour à tous,
Tous les triangles équilatéraux conviennent, et ceux sont les seuls.
Résultat obtenu en utilisant la formule des "trois sinus", les formules d'addition et
sin ^2 x + cos^2 x =1.
 Bonjour et merci pour l'énigme !
Bonjour et merci pour l'énigme !
Je trouve qu'un triangle est raisonnable si et seulement s'il est équilatéral.
Autrement dit, les triangles raisonnables sont ceux dont les côtés sont égaux et strictement positifs et dont les angles sont égaux et mesurent radians.
Je pense qu'ainsi ma réponse est complète.
À bientôt pour la démonstration !
 Bonjour
Bonjour
il me semble que l'un des angles est pi/3.
les triangles équilatéraux correspondent au pb.
Pour ce qui est des autres...
 Bonjour,
Bonjour,
Je vais répondre : "Problème impossible"
Si on commence par se concentrer sur les angles, nous pouvons rapidement nous rendre compte que l'un d'entre eux sera nécessairement égale à  /3. Les deux autres seront donc égaux à
/3. Les deux autres seront donc égaux à  -r et
-r et  +r, r étant la raison de la suite arithmétique.
+r, r étant la raison de la suite arithmétique.
Il n'existe ainsi que 58 triplets d'angles qui auront une progression arithmétique.
Sur ces 58 triplets, aucun ne permet de construire un triangle dont les cotés ont une progression géométrique.
Merci pour l'énigme
 Rebonjour,
Rebonjour,
Voici la démonstration. Je précise que je travaille en radians.
Soit ABC un triangle raisonnable où .
Nous avons donc :
Dans (2)
(3) dans (1)
Nous n'avons pas assez d'informations pour déterminer et
, nous allons donc nous intéresser aux longueurs.
Soient .
BC est le plus petit côté (puisque ).
Et puisque ABC est un triangle raisonnable, alors :
D'après le théorème d'Al Kashi, on a :
Or,
Donc :
C'est une équation bicarrée. Soit . Alors l'équation équivaut à résoudre :
Ce trinôme admet pour discriminant 0 et pour racine double 1.
Donc ou
mais les côtés d'un triangle étant nécessairement strictement positifs pour qu'il existe, alors
.
Les côtés de ABC étant tous égaux, c'est donc un triangle équilatéral et ses angles sont égaux et mesurent radians.
Et pour vérification : les longueurs de ses côtés sont bien en progression géométrique puisque qu'on multiplie à chaque fois par 1 et ses angles sont bien en progression arithmétique puisqu'on ajoute à chaque fois 0.
 Les trois angles d'un triangle raisonnable sont
Les trois angles d'un triangle raisonnable sont avec
et on peut supposer
Autrement si on remplace
par
et par
La somme de ces trois angles est en radians égale à c'est à dire:
donc:
Appliquons la formule d'Al Kashi à notre triangle avec l'angle
Les côtés sont de longueurs avec
et
On se retrouve avec six possibilités qu'on peut grouper en paires:
1) ou
On a l'équation:
C'est à dire:
ou bien
Ces deux dernières équation n'ont qu'une solution réelle positive non nulle:
2) ou
On a l'équation :
C'est à dire:
ou bien
Ces deux dernières équation n'ont qu'une solution réelle positive non nulle:
3) ou
On a l'équation:
C'est à dire:
ou bien
Ces deux dernières équation n'ont qu'une solution réelle positive non nulle:
Ainsi dans un triangle raisonnable les longueurs des côtés sont en progression géométrique de raison égale à 1, c'est à dire que tous les côtés sont égaux et que donc un triangle raisonnable doit être équilatéral.
Réciproquement:
Un triangle équilatéral a tous ses angles égaux à
c'est à dire qu'ils sont en progression arithmétique de raison égale à 0.
En conclusion:
Les triangles raisonnables sont les triangles équilatéraux.
 angle :
angle :
de coté a a a (a
 *+ a>0)
*+ a>0)
et comme
angle : trois angles en progression arithmétique de raison nulle (r=0)
de coté a a a (a
 *+ a>0) les longueurs des côtés sont en progression géométrique de raison 1 (q=1)
*+ a>0) les longueurs des côtés sont en progression géométrique de raison 1 (q=1)
 Merci Jamo pour ces révisions de trigonométrie.
Merci Jamo pour ces révisions de trigonométrie.
Il me semble que l'ensemble des solutions est l'ensemble des triangles équilatéraux, ce qui donne une infinité de solutions;
Donc:
Trois côtés égaux à une longueur quelconque.
Trois angles de Pi/3.
 Bonjour,
Bonjour,
Je trouve qu'il n'existe qu'un seul triangle raisonnable (ou plus précisément, une famille de triangle). Il s'agit des triangles équilatéraux.
Les trois angles valent pi / 3 (progression arithmétique de raison 0. Les côtés sont tous égaux (progression géométrique de raison 1).
Merci pour l'énigme. 
 Bonjour,
Bonjour,
soient A,B,C les angles d'un triangle quelconque et a,b,c les côtés opposés
respectivement à ces angles.
Les angles sont en progression arithmétique cela veut dire que A=A, B=A+r et C=A+2r r étant la raison arithmétique
Comme A+B+C=180° on a A+(A+r)+(A+2r) = 180° il vient A+r=60°
mais la loi des sinus pour un triangle quelconque dit que a/sinA=b/sinB=c/sinC (1)
comme a,b,c sont en progression géométrique de raison R, on peut
écrire a=a b=a*R et c=a*R2
en remplaçant les facteurs de la relation (1) on obtient:
a/sinA = a*R/sin(A+r)= a*R2/sin(A+2r)
on en tire 3 relations a*sin(A+r)= A*R*sinA >>> R = sin(A+r)/sinA
a*sin(A+2r)=a*R2*sinA
a*R*sin(A+2R) = a*R2*sin(A+r) >>> R = sin(A+2r)/sin(A+r)
Les deux valeurs de R trouvées ne sont égales que si r = 0 donc R=1
Cela veut donc dire que les angles A=B=C=60° et que les côtés sont égaux.
La solution de l'énigme comporte tous les triangles équilatéraux dont la longueur des côtés est supérieure à zéro
Bien à vous
 Bonjour jamo,
Bonjour jamo,
Les triangles équilatéraux conviennent, et ce sont les seuls triangles raisonnables.
Démonstration :
Soient les trois angles d'un triangle raisonnable.
Comme leur somme vaut on a
: l'un au moins des angles d'un triangle raisonnable vaut
.
Ensuite, remarquons que si un triangle est raisonnable, il en est de même de tous les triangles qui s'en déduisent par homothétie.
On peut donc prendre pour unité, sans perte de généralité, la longueur d'un quelconque des côtés du triangle.
Soit donc un triangle raisonnable dont un des côtés de l'angle est de longueur 1 et dont les autres côtés sont de longueurs
.

Le théorème d'Al Kashi s'écrit , c'est-à-dire
(*)
La condition pour que les côtés soient en progression géométrique s'écrit soit , soit
, soit
.
En reportant dans (*) on obtient respectivement ,
et
.
Dans chaque cas, la seule solution positive est et donc aussi
, ce qui veut dire que le triangle est équilatéral.
Merci pour l'enigmo 
 Bonjour,
Bonjour,
Les triangles raisonables sont les triangles équilatéraux.
La condition sur les angles impose qu'un des angles soit de 60°. En appliquant le théorème d'Al-Kashi au niveau de cet angle on trouve que le coefficient de la progression géométrique entre les longueur est 1.
 Bonjour
Bonjour
Je propose : tous les triangles équilatéraux, et seulement eux.
(trois angles égaux à 60° donc trois côtés égaux, la longueur du côté quelconque)
 Bonjour
Bonjour
Après plusieurs calculs (et si je ne me suis pas trompé) je n'ai trouvé que les triangles équilatéraux qui répondent à cette énigme (donc avec une progression arithmétique de raison 0 pour les angles et une progression géométrique de raison 1 pour les longueurs).
 Bonjour
Bonjour 
Quitte à effectuer une homothétie, on peut considérer que les côtés du triangle en progression géométrique ont pour longueur 1, q et q².
Par la formule d'Al-Kashi on montre que les 3 angles du triangles ,
et
s'expriment en fonction de la longueur des côtés :
Par ailleurs si on trace dans un repère le petit côté de longueur 1 avec
et
, puis les cercles de centre respectifs
et
et de rayon q et q², alors
le point d'intersection de ces cercles permet d'obtenir tous les triangles de côtés en progression géométrique.
On voit alors naturellement apparaître les racines dérivées du nombre d'or . L'étude se limite ainsi à
et on observe également sans surprise une symétrie par rapport à 1.
Traitons arbitrairement le cas . On montre sans problème que
. Puis, comme on cherche des angles en progressions arithmétique, on impose que :
Une simple étude de fonction suffit à montrer que l'unique zéro est .
Par homothétie on en conclut que seul les triangles équilatéraux vérifient simultanément ces deux propriétés. (Si bien sûr on accepte comme réponse une progression arithmétique de raison nulle)
Merci pour l'énigme 
Clôture de l'énigme
Les seuls triangles raisonnables sont bien les triangles équilatéraux.
dpi : j'ai accepté ta réponse même si elle ne me semble pas très claire et très franche.
Et c'est donc sbarre qui remporte le mois d'avril ! 

 Sbarre
Sbarre
La poisse est fini.

(personne ne sait comment revenir en arrière dans le temps? si oui ça m'intéresse...)

 Merci Chatof
Merci Chatof
La poisse est finie ...
pas vraiment! en fait le jour de l'enigme je partais en vacances et a 3 km de l'hotel, je me suis arrete pour faire 2 courses et me suis fait fracturer ma voiture avec la totale (ordis; appareil photo et objectifs, gopro,... et meme cours de francais de mon fils qui passe le bac!). Apres avoir fait toutes les declarations, retour maison (puisque les clefs de ma fille etaient avec ses papiers avec adresse dessus!). Arrivee a la maison au milieu de la nuit et reponse pour l'enigme uniquement le lendemain au lever. Par chance j'ai mal dormi et me suis leve tot! Au moins le voleur ne m'a pas pique ca (meme si c'est passe tres pres; 30' de plus au lit et c'etait la deuxieme place...).
Félicitations sbarre pour cette première et belle victoire !
Je compatis pour ta mésaventure. J'espère que les choses vont s'arranger pour ton fils.
Pour le reste, c'est vrai que les assurances peuvent rembourser mais ne permettent jamais de récupérer le contenu des ordinateurs (tu avais fait des sauvegardes ?)
 Merci Godefroy,
Merci Godefroy,
les assurances ne remboursent pas un centime (a l'exception du dommage sur le véhicule: la vitre point barre!). Pour les ordis, le mien je m'en fiche un peu, mais c'est celui de ma fille qui a posé un énorme problème. Tout son boulot était dessus et pas de sauvegarde depuis un mois et là ca craint un max (heureusement son dernier projet avait été livré à son client quelques jours auparavant...). Pour mon fils seule sa gopro presque neuve l'a chagriné... (les cours ??? ouais bof ...). L'étape suivante a été de trouver pour ma fille un clavier en azerty! (on habite au Portugal et tous les marchands livrent en France voir Belgique et Suisse mais pas plus loin; on a fini par trouver LDLC qui livre à l'étranger si il y en a que l'info intéresse!).
Enfin une bonne galère quoi!
Nombre de participations : 0
Temps de réponse moyen : 56:36:53.


