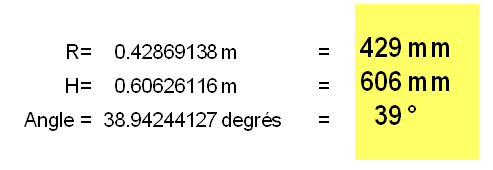Inscription / Connexion Nouveau Sujet
Enigmo 90 : Un problème d'abat-jour, la suite
Bonjour,
pour faire suite à l'énigme précédente ( ![]() Enigmo 89 : Un problème d'abat-jour ), j'ai décidé de proposer une autre forme d'abat-jour à mon décorateur : un simple cône de révolution !
Enigmo 89 : Un problème d'abat-jour ), j'ai décidé de proposer une autre forme d'abat-jour à mon décorateur : un simple cône de révolution !
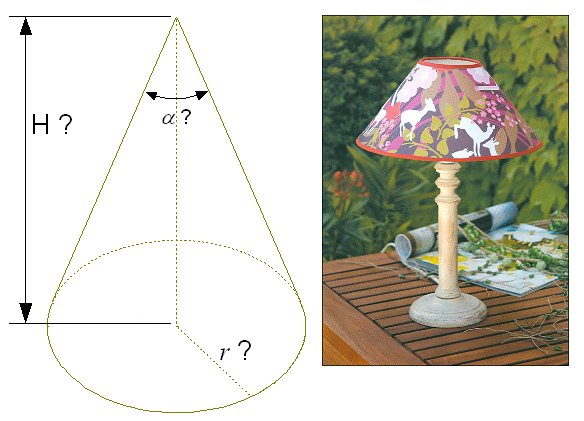
Là aussi et contrairement à la photo, le cône est fermé en haut, et seule la surface latérale est en tissu, et pas le disque de base. Les conditions sont les mêmes : on fixe la surface latérale à 1 mètre carré.
Question : quelles sont les dimensions du cône de révolution afin que son volume soit maximal, sachant que sa surface latérale fait 1 mètre carrée ?
Vous me donnerez 3 nombres en réponse : le rayon de la base et la hauteur du cône, avec une précision de 1 mm pour ces deux longueurs, ainsi que l'angle au sommet du cône avec une précision de 1 degré.
Bonne recherche ! 
 Re-bonjour,
Re-bonjour,
ici, avec les mêmes outils, je trouve :
r=42,9 cm
H=60,6 cm
=
71°
Le tout pour un volume maximal de 116675,015 cm3.
Merci encore.
 bonjour
bonjour
le rayon de la base est 857 millimètres
la hauteur du cône est 606 millimètres
l'angle au sommet est 60 degrés
 Salut jamo,
Salut jamo,
rayon r = 42,9 centimètres, hauteur = 60,6 centimètres,
angle alpha = 70,52 = 71 degrés.
en espérant que ce soit juste !
 Bonsoir Jamo,
Bonsoir Jamo,
Dans cet abat-jour conique, travaillons en mètres pour les distances (et nous convertirons en mm à la fin) et notons S le sommet, O le centre de la base et A un point de la circonférence de la base.
Grâce à un petit coup de Pythagore, on voit que SA, génératrice du cône, vaut
Quant à l'aire du cône, elle vaut
Une façon de calculer cette aire consiste à faire le patron plan du cône en le coupant selon la génératrice SA et en l'aplatissant. On obtient une portion de disque dont le rayon vaut SA. La circonférence complète de ce disque vaut 2 SA, mais nous n'en prenons que 2
SA, mais nous n'en prenons que 2 r, correspondant à la circonférence de la base du cône. Cela nous donne la proportion de disque à considérer :
r, correspondant à la circonférence de la base du cône. Cela nous donne la proportion de disque à considérer : et nous donne l'aire du cône :
.
Cette aire valant 1, nous obtenons la relation {*} :
On remarquera qu'en multipliant cette relation par r2, on obtient {**} :
Le volume du cône vaut .
Il sera maximal ssi l'est, et, comme ce nombre est positif, il sera maximal ssi son carré l'est. On veut donc rendre
maximal.
En utilisant la relation {**}, il suffit donc de rendre maximale.
Une étude classique de variations de cette fonction de r sur ]0 ; + [ nous donne un maximum pour la valeur
[ nous donne un maximum pour la valeur
En remplaçant dans {*}, cela nous permet de calculer la valeur de h correspondante :
En considérant ensuite le triangle SOA, rectangle en O, on a
et donc
En prenant les arrondis demandés, on obtient donc comme solution :
r  429 mm
429 mm
h  606 mm
606 mm

 71°
71°
C'est encore du bel abat-jour ! Il y a de la place chez vous Jamo...
Cordialement à vous tous
Alain
 Bonjour Jamo,
Bonjour Jamo,
ma réponse:
rayon de la base...r = 42,9 cm
hauteur du cône....h = 74,3 cm
angle au sommet.... = 71 degrés
= 71 degrés
volume du cône
Surface du cône
génératrice
rayon du cône
angle au sommet
j'ai trouvé
soit une dérivée
qui s'annule pour
 Bonjour,
Bonjour,
erreur de donnée, j'ai mis la génératrice au lieu de la hauteur
la hauteur est pourtant utilisée dans le calcul de l'angle au sommet
je corrige sans doute un peu tard, tant pis
 rayon de la base : 42.9 cm avec une précision de 1 mm
rayon de la base : 42.9 cm avec une précision de 1 mm
hauteur du cône : 60,6 cm avec une précision de 1 mm
angle au sommet du cônes: 71 degrés avec une précision de 1 degré.
 Enigmo 90
Enigmo 90
Salut jamo
Pour le rayon de la base 429 mm , pour la hauteur 606 mm
et pour l'angle au sommet 71°
 Je suis ravi de cette variante car,j'avais sur le site posé le même problème LE CHERCHEUR D'OR qui voulait savoir comment faire sa coupelle avec 1 m de tôle et un volume maximal.
Je suis ravi de cette variante car,j'avais sur le site posé le même problème LE CHERCHEUR D'OR qui voulait savoir comment faire sa coupelle avec 1 m de tôle et un volume maximal.
donc en retrouvant mes données:
Le cône maximum se construit en enlevant un secteur circulaire de 66°24 SOIT 360-66.24=293°76 quel est le diamètre du cercle complet pour obtenir 1 m2 de surface
+PI *X2/4 = 1*293.76/360 =1.2555 m
donc le coté du cône abat-jour (rayon du secteur) = 1.255/2 soit 61.27 cm
je trouve comme hauteur 35.42 cm
comme rayon de la base 50 cm
Dans ce triangle rectangle (révolution du cône) nous avons l'angle au sommet a tel que cos(a)= 35.42/61.27 = 0.578 soit angle a =54°7
l'angle au sommet du cône sera donc: 109°4
 Bonjour, Jamo
Bonjour, Jamo
Les dimensions du cône de révolution pour que son volume soit maximal sont:
H=607 mm
r=428 mm
 =70°
=70°
Merci pour l'énigme.
 bonjour jamo
bonjour jamo
aire latérale de l'abat-jour r et g en métres
hauteur du cône
volume du cône
on en déduit que V est maximum pour
puis que
et
r=42,9cm à 1millimètre prés par excès
H=60,7cm à 1millimètre prés par excés
 =71°à 1 degré prés par excés
=71°à 1 degré prés par excés
sauf erreur
merci pour cet enigmo
 Bonsoir,
Bonsoir,
je trouve personnellement la solution suivante:
R = 303mm
H= 429mm
et l'angle au sommet 70°,47
Bien à vous
 Bonsoir:
Bonsoir:
Le rayon de la base r 0,4287 m soit environ 429 mm
0,4287 m soit environ 429 mm
La hauteur H  0,6063 m soit environ 606 mm
0,6063 m soit environ 606 mm
L'angle 
 70,53° soit environ 71°
70,53° soit environ 71°
NB: je ne suis pas sûr que l'angle  soit comme l'indique la figure qui suggère tan(
soit comme l'indique la figure qui suggère tan( /2) = r/H
/2) = r/H
Si  correspond à l'angle du patron (étalé,ou "l'éventail", alors ce sera exactement (2
correspond à l'angle du patron (étalé,ou "l'éventail", alors ce sera exactement (2 )/
)/ 3.
3.
Merci pour l'énigme! ça sent le poisson...
 Bonjour Jamo et merci
Bonjour Jamo et merci
Je trouve que le volume est maximal pour
r=0,429 mètre à 1 mm près
H=0,606 mètre à 1 mm près
alpha=71 degrés à 1 degré près
 Bonsoir
Bonsoir
*  ra=1 donc r=1/a
ra=1 donc r=1/a
* a^2=h^2+r^2 donc h^2=a^2-1/(a^2* ^2)
^2)
* V=(1/3)*base*h=(1/3)* *1/(a^2*
*1/(a^2* *
* )*h
)*h
* ... On trouve que V est maximum lorsque
a^4=3/( )^2 donne a=0.742515
)^2 donne a=0.742515
r=0.42869 m
h=0.60626 m
r/h=tan( /2);
/2); =70.5287
=70.5287
Réponses: r=429 mm
H=606 mm
 =71 degrés
=71 degrés
Merci
Clôture de l'énigme
Dans ce problème, on peut encore remarquer que le rapport entre le rayon et la hauteur est égal à  2.
2.
J'ai eu l'idée de ce problème suite à un article lu il y longtemps je ne sais plus où (dans un magazine tangente je crois), où l'on cherchait le tipi indien optimal, qui présente le maximum de volume pour le minimum de toile. Et il se trouve que les dimensions des tipis vérifient à peu prés ce rapport de  2 ...
2 ...

J'avais pourtant la bonne réponse H=60,6cm la preuve c'est que j'ai calculé le volume avec la bonne valeur
je me suis simplement trompé de ligne à la copie et je m'en suis rendu compte 1 heure après.
de toute façon je me plie à la décision du juge
merci pour ces énigmes fort intéressantes
Nombre de participations : 0
Temps de réponse moyen : 110:22:33.