Inscription / Connexion Nouveau Sujet
Enigmo 1 : Périmètre minimum 
Bonjour,
voici la première énigme à jamo, la première Enigmo !
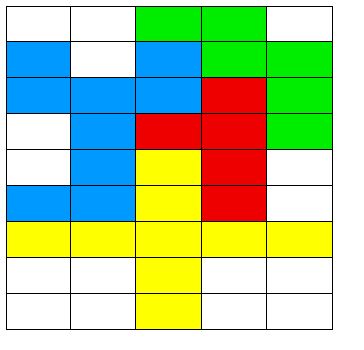
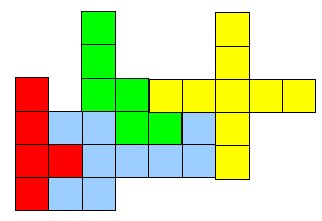
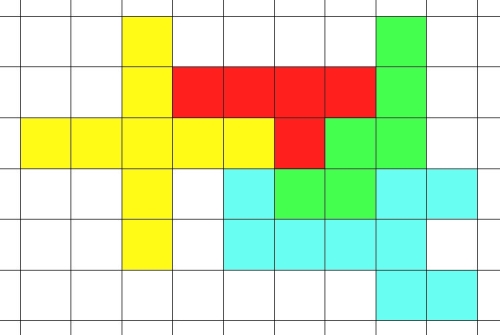
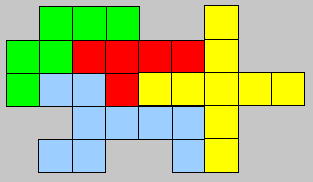
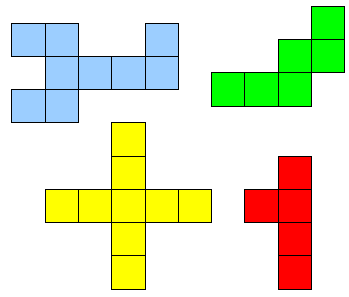
Assemblez les quatre pièces ci-dessous en une figure dont le périmètre soit le plus petit possible.
Vous donnerez la valeur du périmètre ainsi que la preuve en image.
Règles à respecter :
- ne pas superposer les pièces
- chaque pièce peut être tournée et retournée
- pas de trou complètement encerclé entre les pièces
- pour le calcul du périmètre, chaque petit carré à un côté égal à 1
A vos ciseaux !!
 sakut, bravo Jamo pour cette première Enigmo
sakut, bravo Jamo pour cette première Enigmo
je propose 36
Par contre comme j'ai pas d'apareil photo numérique, je ne peux pas photographier mon découpage^^ donc je fait un dessin avec le clavier:
X
X
X X
J J X X J O
J J J J O
J J K O O O O O
K K K K O
O
J'espère que c'est clair
Bonne journée
 Bonjour jamo
Bonjour jamo
Tout d'abord félicitation pour ton nouveau grade bien mérité !!  .
.
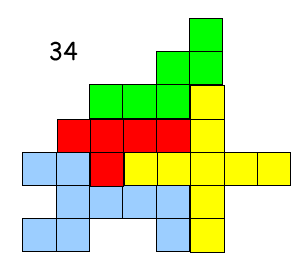
sans être sûr je réponds 34.
merci pour l'énigme  .
.
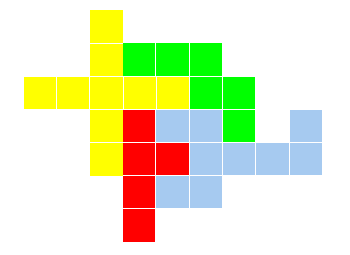
voici la preuve en image
 Bonsoir,
Bonsoir,
Et félicitations Jamo pour ta première énigme 
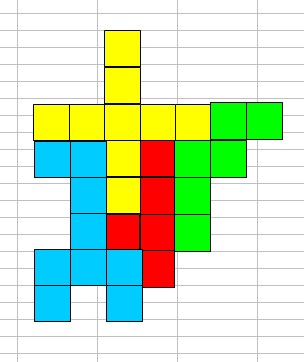
J'ai trouvé deux solutions possibles avec un périmètre de 36 :
 Bienvenue et merci à l'énigmatique Jamo.
Bienvenue et merci à l'énigmatique Jamo.
La somme des périmètres des 4 formes est 66. Le périmètre d'un assemblage est donc 66-2S, où S est la somme des longueurs des segments faisant frontière entre deux formes.
(Remarque au passage: le périmètre de l'assemblage est un nombre pair.)
Pour que l'assemblage ait un périmètre minimum, il faut donc que S soit maximum.
Je ne sais pas continuer autrement que par tâtonnement, en assemblant les formes découpées dans du papier.
J'arrive à faire un assemblage (et même plusieurs) où S=16 et je n'arrive pas à faire mieux.
Comme 66-2.16=34, je propose 34 comme périmètre minimum.
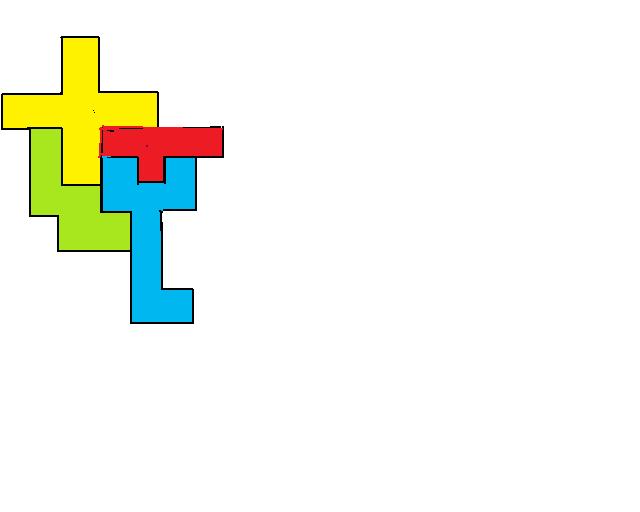
Ce n'est pas la note qui compte, c'est le résultat


J'adore le poisson, ça rend intelligent.
*challenge parti chez le géomètre-expert*
 Bon va pour 34 de périmètre
Bon va pour 34 de périmètre
sans conviction pour la meilleure solution mais en bougeant les pièces j'ai pas mieux 
 bonjour,
bonjour,
je propose 34 unités de longueur pour le périmètre minimun (sans conviction,plusieurs dispositions donnent le même périmètre mais est ce bien le minimun?)
00003
00003
2233333
0224311
002431
002441
0004111
0000101
(1)=bleu
(2)=vert
(3)=jaune
(4)=rouge
la pièce bleue a été retournée
merci pour cette distraction
 Bonjour,
Bonjour,
Le genre d'énigme que j'aime !
Ceci dit, je ne suis pas fier de moi.
Pas réussi à descendre en-dessous de 34 de périmètre.
A+
Voilà plus de 15 jours que l'énigme a été soumise, plus de réponse depuis 3 jours : il est temps de corriger ! 
Relativement peu de participations pour la 1ère Enigmo. Même si le principe en était évident et abordable même en école primaire (d'où l'unique étoile affectée à l'énigme), il est vrai qu'on n'est jamais certain de donner la bonne réponse dans ce genre d'énigmes (difficile à démontrer que le résultat obtenu est optimal)
Bravo à tous ceux qui ont trouvé la bonne réponse qui était bien un périmètre minimum de 34.
On peut d'ailleurs remarquer qu'il existe plusieurs solutions.
Si quelqu'un veut s'amuser à dénombrer le nombre de solutions, qu'il ne se prive pas ! 
keriatsu >> ta pièce verte n'est pas bonne, ce qui explique que ta réponse n'est pas acceptée. Comme quoi il aurait mieux fallu de découper les pièces ! 
Ansgard >> ta réponse est encore une illustration de ton extrême maturité. Ca ne mérite même pas que je te mettre un poisson, je préfère ignorer ce genre de manifestation. A l'avenir, merci d'éviter de venir polluer aussi les énigmes en plus des messages dans lesquels tu interviens déjà.
A la prochaine pour la prochaine Enigmo ou correction ... 
 Voici une des énigmes dont je doutais énormément de ma réponse, il en reste encore 3 qui me font peur, j'éspère que tout ira bien
Voici une des énigmes dont je doutais énormément de ma réponse, il en reste encore 3 qui me font peur, j'éspère que tout ira bien 
 Une question à jamo (et à vous tous) me tracasse;
Une question à jamo (et à vous tous) me tracasse;
Peut-on démontrer que 34 est effectivement le minimum?
J'ai une idée de démarrage. J'implore à l'avance votre clémence si, malgré votre aide, cette idée n'aboutit pas.
Par l'absurde: Supposons que le minimum est strictement inférieur à 34.
Il existe donc un assemblage où la somme S des longueurs des segments appartenant à une frontière commune à deux zones est supérieure ou égale à 17.
Comme il y a 4 pièces, le nombre de frontières communes à 2 zones est au maximum de 6.
Il semble clair (mais il faudrait une justification propre) qu'on ne peut faire un assemblage où chacune des 4 zones longe chacune des 3 autres.
Le nombre de frontières communes à 2 zones est donc au maximum de 5.
L'une de ces frontières communes utilise donc au moins 4 segments.
On prend donc les pièces 2 par 2 et on regarde si on peut les accoler de façon à avoir une frontière commune de longueur 4 ou 5 (on ne peut faire mieux?)
J'espère limiter ainsi les tâtonnements...
Merci d'avance pour votre aide.
Ansgard >> ta réponse est encore une illustration de ton extrême maturité. Ca ne mérite même pas que je te mettre un poisson, je préfère ignorer ce genre de manifestation. A l'avenir, merci d'éviter de venir polluer aussi les énigmes en plus des messages dans lesquels tu interviens déjà.

Tu verras jamo, tu finiras par noter aussi ce genre d'individus ne serait-ce que pour voir afficher en bas "45 notes attribuées sur 45 participants"

Parfois on en oublie...
rogerd >> j'avoue ne pas avoir d'idée pour démontrer que 34 est effectivement le minimum.
On pourrait imaginer un programme qui réalise tous les assemblages possibles ...
 J'espère que le courrier de Minkus ne m'est pas destiné? Je ne voudrais pas passer pour un "genre d'individu"?
J'espère que le courrier de Minkus ne m'est pas destiné? Je ne voudrais pas passer pour un "genre d'individu"?
A destination de jamo: merci d'avoir pris mes remarques en considération.
Tout-à-fait d'accord pour utiliser l'informatique et se fier aux résultats donnés par un programme.
Votre problème me paraît un bon exemple de ce qui pourrait déboucher sur une situation enrichissante;
* en faisant appel à ceux qui savent analyser une situation et diminuant le nombre de cas possibles (les "intéllos")
* en faisant appel à ceux qui savent mécaniser une situation abstraite (les "informaticiens").
Mais j'ai peur de ne faire partie d'aucune des deux catégories...
J'appelle donc à nouveau chacun des participants à s'attaquer à votre problème précis.
 Bonsoir Rogerd,
Bonsoir Rogerd,
je pense que Minkus parlait d'Ansgard et de sa réponse complètement loufoque (voir le post du 06/02/2008 à 14:31 et la remarque de Jamo à ce sujet dans le message de correction de l'énigme).
Ta question est très intéressante, au contraire (cependant, je n'ai pas d'idée pour y répondre  )
)
On pourrait aussi de poser une autre question : et si on autorise les "trous" dans l'assemblage, quel est le périmètre minimal qu'on peut trouver ? (périmètre exterieur, ou en prenant en compte le périmètre des trou)
 Bonjour
Bonjour
suite à ce que j'ai posté dans ce lien ![]() ENIGMA 12: La liberté affreuse !, et pour répondre à la demande de Rogerd je vais essayer d'expliquer les idées sur lesquels je me suis basé pour dire que la réalisation du programme est possible:
ENIGMA 12: La liberté affreuse !, et pour répondre à la demande de Rogerd je vais essayer d'expliquer les idées sur lesquels je me suis basé pour dire que la réalisation du programme est possible:
Avant tout je dois préciser que le language que j'utilise est le C++:
Pour commencer le programme la première chose qui vient à l'esprit c'est quels variables on doit utiliser pour représenter nos 4 figures, j'ai pensé donc à une class figure mais avant de definir ma class je vais expliquer quelques termes que j'utiliserai après:
une figure est l'assemblage de segments horizontaux et verticaux.
un segment est constitué de 2 points distincts
l'origine d'une figure est le point le plus haut de la figure situé à gauche, à partir de ce point est du numéro de la figure notre class sera capable de dessiner la figure.
et voilà maintenant le corps de la class figure:
class figure {
point origine;/*point est une structure qui aura la forme suivante:
struct point{
int x;
int y;
}*/
segment seg[];
int nseg;
*/une figure sera un tableau de "nseg"segments, un segment est une structure definit ainsi:
struct segment{
point P1;/*point de départ*/
point P2;/*point final*/
}*/
public:
void figure(point orig,int num)
{origine=orig;
if(num==0){/*on prendra la figure jaune par exemple comme figure num0, tout ce qu'on a à faire c'est la dessiner*/
seg[0].P1=orig; seg[0].P2.x=orig.x + 1; seg[0].P2.y=orig.y;
seg[1].P1=seg[0].P2; seg[1].P2.x=seg[0].P2.x; seg[1].P2.y=seg[0].P2.y - 2;
.
.
.
/*jusqu'à arriver à seg[11]*/
seg[11].P1=seg[10].P2; seg[11].P2=orig;
nseg=12;}
else if(num==1){/*on dessine la figure bleu*/}
else if(num==2){/*on dessine la figure bleu en faisant une rotation de 90°*/}
else if(num==3){/*on dessine la figure bleu en faisant une rotation de 180°*/}
else if(num==4){/*on dessine la figure bleu en faisant une rotation de 270°°*/}
else if(num==5){/*on dessine la figure bleu en inversant la face*/}
.
.
else if(num==8){/*on dessine la figure bleu en inversant la face et en faisant une rotation 270°*/}
.
.
.
else if(num==32){/*on dessine la figure rouge en inversant la face et en faisant une rotation de 270°*/}
}/*et voilà le constructeur de figure est terminé*/
/*on pourra ajouter d'autres variables comme:
segment seghaut[] /*seghaut contiendra les segments horizontaux dirrigé vers le haut*/
segment segbas[]
segment segdroite[]
segment seggauch[]
/* ces variables seront peut être utiles dans notre boucle de recherche à la suite*/
/* on ajoutera aussi les variables suivant que j'expliquerai leur utilité aprés*/
point Ph;/*c'est le point le plus haut dans une figure donnée*/
/*de même*/ point Pb;point Pd;point Pg;
};
________________________
maintenant notre class figure est bien définit, il reste une class figcomp qui aura à peu près le corp suivant:
class figcomp{
point orig;
segment seg[]:
int nseg;
figure fig[];/*qui contiendra les figures présent dans figcomp*/
int nfig;/*le nbre de figures présent dans dans figcomp*/
int perimetre;
/*pui on fait declarer les extrémité de la figcomp tout comme on a fait dans ce qui précède*/
public:
void figcomp(){/*dans le constructeur on fait initialiser par la figure 0 dans le point origine (14,17)*/}
void ajout(figure fig1)
{/*on ajoute une figue pour la première fois, en fixant son origine dans une position bien déterminé dont on trouvera une formule, y aura une grande bataille la dessus  */}
*/}
void tourne()
{/*cette fonction deplacera (voir tournera) la dernière figure ajouté dans la position suivante, cette fonction est aussi que celle qui la précède, voir un peu plus dur*/}
void suppr()
{/*cette fonction supprime une figure de la figcomp*/}
/*à chaque fois qu'on utilise une de ces fonction on met ajour nos variables privée*/
};
Les classes dont on a besoins sont définit il restera la boucle qui cherchera la solutions optimale qu'on sait déjà qu'elle est <=34, voici une idée sur les étapes de cette boucle:
1/On fixe L'origine de la figure 0 (jaune) dans le point (14,17)
2/On fait tourner une des 3 autres figure(pas la peine pour l'instant de faire une rotation de la figure ajouté ou de d'inverser sa face puisque la figure jaune et parfaitement symetrique)
3/On prend les 16 figures qui restes une par une, et on fait tourner chacune d'eux en partant de l'origine jusqu'à revenir à lui dans le sens d'une montre)
4/On prend les 8 figures qui restes une par une, et on fait tourner chacune d'eux autour de la figure composé en partant de l'origine jusqu'à revenir à lui dans le sens d'une montre.
Pour minimiser les calculs et éviter les répition, on pourra faire les tests suivants dans chaque étape à partir de l'étape 2:
-/supposant qu'on a utiliser la pièce 8 dans l'étape 2, et qu'on a teminer tout les cas possibles avec cette pièce, on passe alors à la pièce 9 dans l'étape 2, pour éviter les répitions, la pièce 8 ne doit en aucune étape qui suit avoir un contacte avec la pièce 0.
plus generalement: une pièce d'indice p qui est ajouté dans une étape n n'a pas le droit d'avoir un contact avec une pièces d'indices p'vérifiants les 2 conditions suivantes:
1)la pièce p' est ajouté dans une étape n' tel que n'< n-1
2)dans l'étape (n'+1) on a ajouté une pièce p1 tel que p1 > p.
Ces 2 conditions permetteront d'élliminer la répition des figures composés.
-/on calcul le périmetre minimal qui puisse être réalisé entre les extrémité de la figure composé en utilisant la formule suivante:
Per = (Pd.x-Ph.x)+(Ph.y-Pd.y) + (Pd.x-Pb.x)+(Pd.y-Pb.x) + (Pb.x-Pg.x)+(Pg.y-Pb.y) + (Ph.x-Pg.x)+(Ph.y-Pg.y)
si (Per>34) pa la peine de passer à l'étape suivante, il faut passer au cas suivant dans l'étape actuelle.
-/ enfin si on est dans la dernière étape on calcule le perimetre si jamais on trouve une disposition permettant de trouver un pèrimetre<34 (ce qui me surprendra) on l'affiche.Pour calculé le perimetre il suffit d'ajouter le peimetre de la figur ajouté à la figure composé - 2*la longueur des segments communs.
voici à peu près mon idée sur le programme qui malgré qu'il soit très compliqué me parait réalisable.
En tout cas comme je l'ai déjà dit dès que les vacances arrivent j'essayerai de le réaliser et je vous tiendrai au courant  ,.
,.
 Pour juste expliquer l'idée il m'a fallu 2 heures, vous pouvez donc imaginer ce qu'un tel programme necessite en matière de temps pour être réalisé, ca fait pousser les cheuveux blancs
Pour juste expliquer l'idée il m'a fallu 2 heures, vous pouvez donc imaginer ce qu'un tel programme necessite en matière de temps pour être réalisé, ca fait pousser les cheuveux blancs  .
.
 Merci à master_och pour sa recherche déjà bien détaillée.
Merci à master_och pour sa recherche déjà bien détaillée.
Je ne pratique pas le C++ mais on comprend les idées à la lecture .
Je pense pouvoir traduire cela en Maple.
Bonne idée de définir plusieurs exemplaires d'une même figure (après rotations ou symétries).
Comme prévoit master_och, il y aura une grande bataille pour choisir le point d'ancrage des figures à partir de la deuxième...
Gros travail en perspective!
 Moi je pratique pas Maple, mais si tu pourra traduire cette idée ce sera vraiment génial car ce qui te reste à faire est beaucoup plus difficile, en tout cas s'il y a quelque chose dans mon explication qui te parait un peu ambigu je serai près à reexpliquer.
Moi je pratique pas Maple, mais si tu pourra traduire cette idée ce sera vraiment génial car ce qui te reste à faire est beaucoup plus difficile, en tout cas s'il y a quelque chose dans mon explication qui te parait un peu ambigu je serai près à reexpliquer.
Bon courage !  .
.
 Bonjour!
Bonjour!
J'essaie de creuser les idées de master_och.
Déjà, un problème:
J'ai mes deux formes , définies chacune par une suite de segments et je veux les assembler. Je translate la deuxième de sorte qu'elle démarre sur un des sommets de la première. Comment vérifier qu'elle ne va pas passer au travers de la première?
Autrement dit: comment tester que les deux formes ne vont pas empiéter l'une sur l'autre?
 Peut-être une idée:
Peut-être une idée:
A chacune des 4 formes (pièce élémentaire du puzzle) on associe l'ensemble des points de la pièce qui sont à l'intérieur de cette pièce (en s'en tenant aux sommets des petits carrés qui forment la pièce). Dans l'exercice à traiter, ces ensembles sont assez réduits.
Pour que les deux pièces qu'on assemble d'abord ne se chevauchent pas, il faut et il suffit que le contour de la deuxième ne passe par aucun des points intérieurs à la première.
Je sens qu'on va y arriver!
 Bonsoir rogerd
Bonsoir rogerd
J'ai une autre idée qui me parait mieu:
2 piéces élémelntaires se supperposent ssi un segment vertical de la frontière de la première coupe un segment horizontal de la frontière de l'autre, et c'est déjà une utilité des variables seghaut[],segbas[], segdroite[] et seggauch[]que j'ai proposé dans la class figure.
supposant que seg1 et seg2 sont respectivement 2 segment vertical et horizontal, ces 2 segments se coupent ssi seg2.P1.x<seg1.P1.x=seg1.P2.x<seg2.P2.x et seg1.P1.y<seg2.P1.y=seg2.P2.y<seg1.P2.y .
Il faut quand même penser à minimiser les calculs car la vitesse du processeur est limité.
Pour l'instant on a environ 3 x (nbre de rotation autour de la figure de la pièce 0)x16 x (nbre de rotation autour de la figure de la pièce composé)x 8 x (nbre de rotation autour de la figure de la pièce composé) cas à traiter, chaque cas aura un certain nbre d'instructions élementaire à effectuer, donc on doit minimiser le nbre d'instructions du mieu qu'on peu car avec un proc de 3Ghz (par exemple)on pourra pas depasser 3x230~ 3x109 instructions/sec.
Essaies de tenir en compte cette contrainte  .
.
 Bonjour à tous.
Bonjour à tous.
Une autre idée:
On pourrait définir une figure, non pas par sa position dans le plan, mais par la suite des actions qu'on commet en parcourant le pourtour dans le sens horaire:
-1 pour "tourner à gauche", 0 pour "aller tout droit", +1 pour "tourner à droite".
On s'affranchirait ainsi des déplacements.
Quant à la figure "retournée", on l'obtient en échangeant les +1 et les -1.
A partir de là, j'ai des idées pour construire les assemblages.
A l'attention de Jamo: Si vous considérez que ces échanges n'intéressent que trop peu de mathiliens, n'hésitez pas à intervenir!
A l'attention de Jamo: Si vous considérez que ces échanges n'intéressent que trop peu de mathiliens, n'hésitez pas à intervenir!
Vous pouvez continuer, du moment que ça intéresse ne serait-ce que 1 ou 2 personne, je n'ai rien à dire ...

 Bonjour
Bonjour
J'ai pas très bien compris ton idée rogerd, mais bon si cela t'inspire n'hésite pas à essayer, mon idée n'est qu'une proposition  .
.
 Bonjour master_och
Bonjour master_och
Je précise en prenant l'exemple de la figure rouge. Elle serait définie par la suite:
0,0,0,+1,+1,0,-1,+1,+1,-1,+1,+1 ou bien par la suite
0,0,+1,+1,0,-1,+1,+1,-1,+1,+1,0 etc (tout dépend du point où on commence le parcours).
Es-tu d'accord jusque là?
 Re
Re
Oui sava j'ai compris ton idée, mais je vois pas comment ca simplifiera l'assemblage, peux-tu expliquer 
 Bonjour master_och
Bonjour master_och
Je veux assembler deux formes A et B associées à sA et sB, suites de nombres valant -1,0 ou 1.
A partir de sB, je définis (c'est facile) sB', analogue à sB, qu'on obtient en contournant B dans le sens antihoraire.
On choisit le point de départ imposé à la frontière commune, à la fois sur le contour de A et sur le contour de B. Cela fait pas mal de possibilités mais, pour la plupart, elles vont tourner court. En effet, si l'on veut que la frontière commune ait une longueur de 3 au moins (le nombre 3 m'intéresse vu les réductions du problème) il est nécessaire que les deux suites prennent la même valeur au point d'ancrage et au point suivant. Il est nécessaire aussi qu'au point qui est juste avant le point d'ancrage et au point qui est à la fin de la frontière commune, la valeur de sB' soit plus grande que sA. La condition est nécessaire mais pas suffisante (il reste des cas tordus de chevauchements), mais comme cette condition est très forte et vu l'exemple qu'on traite, je pense qu'il y aura peu de solutions et qu'on pourra éliminer visuellement les solutions parasites.
J'ai commencé de livrer ça à Maple. Pour l'instant, il sait dessiner une pièce quelconque à partir d'une suite associée dont les termes valent -1,0 ou 1. Je m'attaque à l'assemblage de 2 pièces.
Je te tiendrai au courant.
 En fait j'ai pas très bien compris, mais bon ca parait interessante ton idée. Je vais pas te gener en demandant des explication à tous, l'essentiel c'est que j'ai compris l'idée general, et surtout que je me sens plus à l'aise lorsque je compte sur mes propres reflexions plutot que d'apprendre les idées des autres.
En fait j'ai pas très bien compris, mais bon ca parait interessante ton idée. Je vais pas te gener en demandant des explication à tous, l'essentiel c'est que j'ai compris l'idée general, et surtout que je me sens plus à l'aise lorsque je compte sur mes propres reflexions plutot que d'apprendre les idées des autres.
Bonne continuation à toi  !
!
 2 pièces se superposent si on met l'une au dessus de l'autre
2 pièces se superposent si on met l'une au dessus de l'autre  , pour generer le programme il faut éviter ces cas ...
, pour generer le programme il faut éviter ces cas ...
Bonjour à master_och et à rogerd !
Il semble urgent d'utiliser des matrices...J'ai déja programmé un tétris mais le programme que vous semblez vouloir faire est 1000 fois plus complexe...
Voici le nombre de pièce possible en fonction du nombre de case (je ne pense pas avoir fait d'erreurs):
1 case -> 1 piece
2 cases -> 1 piece
3 cases -> 2 pieces
4 cases -> 5 pieces
5 cases -> 13 pieces
Il faudrait mettre ces différentes formes en un ensemble de chiffre et trouver un algo... ( 2 mots = 3000 heures de reflexion  )
)
matovitch
PS: Si c'est une suite quelle est-elle (pas de réponses trouvées sur le net...)
Nombre de participations : 0
Temps de réponse moyen : 105:13:07.