Inscription / Connexion Nouveau Sujet
Ensemble de définition
Hello 
Je regarde un exercice dans le livre "Method'S" (terminale S), et un moment il dit que l'ensemble de définition de f(x) = x
x est [0, +infini[.... et que x est défini sur ]0, +infini[...
Pouvez vous m'expliquer pourquoi ces ensembles de définition ?
Je vous remercie.
@+
Erwan
Bonjour,
la racine carrée est définie sur [0,+infini[ donc ce qui est dit dans ton bouquin est faux, (sauf s'il est dit "défini et dérivable sur...")
L'ensemble de définition d'une fonction c'est tout bête, c'est l'ensemble sur lequel on a que ta fonction est bien définie.
Par exemple ici, f(x) avec x qui est négatif, ne peut pas exister, car la racine carré d'un nombre négatif n'existe pas dans R (et ne se prolonge pas de manière unique dans C)
C'est le même principe que 1/x avec x qui est nul, ca n'existe pas.
A+
Merci Otto,
Toutefois, je vais recopier l'énoncé pour que çà soit plus clair :
(Chapitre 2 du livre^^) :
Déterminez la dérivée de f telle que f(x) = xx.
L'ensemble de définition est [0;+infini[, mais comme x n'est dérivable que sur ]0;+infini[, on ne peut appliquer les formules que sur ]0;+infini[,
Merci 
Oui, en fait ce que racconte le bouquin n'est pas extremement exact au niveau de la justification, mais c'est bien ca.
C'est ce que je te disais, l'ensemble de définition de f n'est pas celui de f'.
A+
On utilise la dérivée de u(x)v(x) soit u'(x)v(x) + u(x)v'(x).
On trouve après quelques calculs : f'(x)= 3/2x.
Au fé pourquoi ne peut on pas faire 0 ?!
f(x) = x.Vx
f(x) = x^(3/2)
f '(x) = (3/2).x^((3/2)-1)
f '(x) = (3/2).x^(1/2)
f '(x) = (3/2).Vx
-----
Je ne vois pas pourquoi on ne pourrait pas dériver en 0.
Même si la dérivée à gauche de 0 n'existe pas.
Moi je trouve
Mais ta solution est elle
ou
La racine carré de 0 est 0 donc existe
C'est la dérivé de qui est défini sur ]0;+OO[ car sa dérivé est
Dites moi si je me trompe
Skops
"Je ne vois pas pourquoi on ne pourrait pas dériver en 0."
On peut dériver à droite en 0 comme tu le dis JP.
L'idée, c'est que l'on défini en général la dérivée sur des ouverts, et [0,+oo) ne l'est pas, et (0,+oo) en est un, notamment c'est même le plus grand inclus dans le précédent.
C'est juste une petite subtilité.
En fait, pour ma part je répondais à une questio non posée, celle de la racine carrée et non de x->x*racine(x).
A+
Bonjour à tous
Erwan , si tu regardes bien ce qu'il y a ensuite dans le bouquin , ils mettent :
Le travail n'est pas fini ! : Il se peut quand même que f soit dérivable en 0 puisqu'elle y est définie.
Et la il démontrent la dérivabilité de f en 0
Puis ils mettent :
Conclusion : Il n'y a pas d'erreur , n'est pas dérivable en 0 et pourtant
l'est
Jord
ui Nightmare ^^,
j'ai de quoi bosser avec ce bouquin, en plus j'ai pris l'interro des lycées !
@+
Erwan
>erwan
pour compléter le post de NM de 14:24
un ptit dessin pour visualiser les dérivées en 0
Philoux
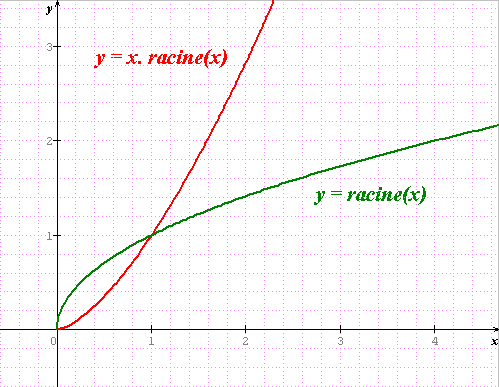
Euh Philoux, on ne voit pas les dérivées sur ton dessin ?! par ex (3/2)*x
Merci en tout cas.
Tu as raison erwan sur le fait que les (fonctions) dérivées ne sont pas indiquées.
En revanche, le nombre dérivé (qd il existe) en 0 est la pente (qd elle existe) de la tangente à la courbe.
ET ça, tu dois le "voir", voire l'estimer...
Tu saisis cette histoire de nombre_dérivé et pente de tangente ?
Philoux
J'ai du mal à saisir ceci :
" le nombre dérivé (en 0) est la pente de la tangente"
Je crois que je vais revoir mon cours 
>erwan
lis ceci 
Cours sur les dérivées et la dérivation, au paragraphe 5
Philoux
Dans ce cas présent, le nombre dérivé est bien 0 ?!
Pour quelle fonction ?
y = f(x) =x.racine(x)
ou
y = g(x) = racine(x)
Philoux
oui
je te fais des courbes complémentaires pour bien voir les fonctions dérivées
Philoux
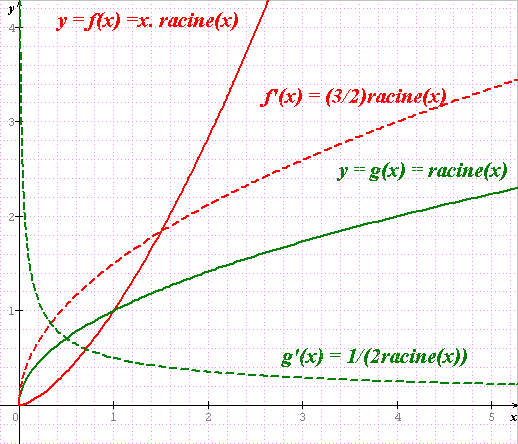
>erwan
Cette fois-ci, les courbes en pointillés sont les fonctions dérivées des fonctions initiales.
Tu vois que pour x=0 :
f'(0) = 0 d'où la tangente horizontale pour f
g'(0) n'existe pas et tend vers +oo, d'où la "tangente verticale" pour g
C'est plus clair ?
Philoux
oulà je confondais asymptote et tangente un moment lol
Je comprends mieux.
cool l'ile aux mathématiques 
Salut
Je reviens sur la non dérivabilité de la fonction racine carrée en 0
Je crois que cette non dérivabilité doit être montrée directement et non pas déduite du fait que la formule donnant cette dérivée n'est pas appliquable en 0
D'une façon générale , comme le rappelle Erwan , la dérivabilité doit être montrée avant d'appliquer la formule
jean-émile
J'ai encore deux questions :
N'est on pas en présence d'asymptotes plutôt que des tangentes ?
quand on regarde la fonction g et sa dérivée, elles ne sont pas du tout à proximité, elles ne partent pas d'un même point ?! pk dis t-on que c'est sa dérivée alors ?!
Je préfère bien comprendre tant qu'à faire lol et je ne veux pas vous importuner
Erwan, que sais tu des dérivées?
Jean Emile, très bonne remarque, c'est justement une erreur fréquemment commise, et en fait si la "formule" n'est pas définie en 0, ca ne montre rien. En général c'est une erreur souvent commise par les élèves et certains profs, et c'est important de le souligner.
>Erwan 17:18
vas sur le site en cliquant où il y a les ptites mains...
Les notions d'asymptotes sont aussi expliquées..
x=0 est asymptote verticale pour g'(x)
Philoux
Otto,
Je connais les formules mais je veux approfondir pour bien comprendre ce que c'est parce que j'ai fait çà "bêtement"...
Je vais trouver.
Merci
Ok, il faut que tu comprennes qu'avant que ce soient des formules, c'est un opérateur important:
A une fonction (dérivable) il te donne la fonction f' qui représente la variation de f.
f'(x)= coefficient directeur de la tangente à f au point x.
On peut facilement se convaincre que f'>0 sur I implique f croissante sur I et f'<0 sur I implique f décroissante sur I, où I est un intervalle de R.
Salut otto
...si la "formule" n'est pas définie en 0, ca ne montre rien...
Tu aurais des exemples et/ou des contre-exemples, stp ?
Philoux
Oui, il y'a le classique:
f définie sur R par
f(x)=cos(1/x)x²
f(0)=0
f est elle continue sur R*? en 0? dérivable sur R*?
Calculer f' sur R*.
f est elle dérivable en 0?
1) La fonction du premier message est un exemple.
2) La fonction f : x ----> x * |x| est définie et dérivable sur 
Elle est dérivable en 0 , malgré la formule
La dérivée en tout point x de : f ' : ----> (3 * |x|) / 2
jean-émile
ah j'ai bien compris ton post de
17:29 otto !
Merci beaucoup !
je dirais alors :
le cos(1/x) oscille entre -1 et 1 mais fois x² => continue en O (?)
f'(x)=2xcos(1/x)+sin(1/x)
f'oscille entre -1 et 1 => f non dérivable en 0 (?)
ahhhhhhhh tu veux me faire calculer limite (f(x)-f(0)/(x-0) qd x->0
xcox(1/x) qui td vers 0
donc f dérivable en 0 (?)
Je pencherai pour cette dernière formulation.
Philoux
C'est pas rigoureux, mais l'idée est là.
Notamment f'(x) ne tend pas vers 0 en 0 d'après la vraie définition de la limite (et pas une fausse qu'on pourrait trouver dans le Monier par exemple...) et pourtant f'(0) existe.
Notamment, on a un bel exemple de fonction dérivable mais non C1 et non prolongeable en une fonction C1.
f'(x) ne tend pas vers 0 en 0
on doit donc écrire f'(0) égale 0 ?
Philoux
Oui parce que c'est bel et bien égal.
Mais f' n'est pas continue en 0.
limite de f'(x) lorsque x->0
n'existe pas ici.
En fait ici, on doit avoir une singularité essentielle en 0, c'est à dire que si je me donne un nombre complexe z, alors je peux toujours trouver une suite (zn) qui converge vers 0 et telle que
f(zn)->z
C'est quelque chose d'extremement plus fort que de ne pas être continue en 0.
Tu peux vulgariser/traduire ou ça demande d'autres bases en pré-requis ?
Philoux
Salut,
oui j'ai traduit:
tu te donnes un nombre complexe, mettons z=i.
Alors si je prolonge f à C tout entier par la même formule:
f(z)=z².cos(1/z)
Alors je peux trouver une suite (zn) qui tend vers 0 et pourtant
f(zn) tend vers i
Si je me donne un autre nombre complexe, mettons w=4, alors je peux encore trouver une autre suite (wn) qui va tendre vers 0 et telle que
f(wn) va tendre vers 4.
Etc
Je peux le faire pour n'importe quel nombre complexe z.
Si ma fonction est continue alors pour TOUTE suite (zn) qui tend vers 0, f(zn) tend vers f(0).
La négation de ceci serait que IL EXISTE une suite (zn) qui tend vers 0 et telle que f(zn) ne tend pas vers f(0).
Ici j'ai quelque chose de pire:
je me fixe un z quelconque, et je peux lui associer une suite (zn) qui tend vers 0 et telle que f(zn) tend vers z.
C'est un théorème très puissant, et qui porte le nom de deux auteurs dont j'ai malheureusement oublié le nom, je vais essayer de le retrouver.
A+
otto
c'est quoi cette histoire de Monier :
Ici on a bien comme tu dis :
f '(x) = 2*x*cos(1/x) + sin(1/x) si x non nul
f '(0) = 0
f ' n'a pas de limite en 0
Je ne vois pas en quoi ça gêne ??
jean-émile
Il y'a Weierstrass qui est auteur de ce résultat, mais il me semble que ce théorème n'était pas exclusivement de lui. Enfin ce n'est pas très important.
Ici, voir que l'on a une singularité essentielle se voit en fait très facilement si on connait un peu de théorie des fonctions complexes.
Au voisinage d'une singularité isolée s, si on a une fonction complexe f et dérivable autour de s, alors on peut toujours développer f en "série de Laurent":
f(x)=
Zai(x-s)i
sur un petit disque D épointé et centré en s.
Ici on va prendre pour définition que s est une singularité essentielle si pour j<0, il existe un i<j tel que ai
0.
Mais on va éviter de trop rentrer dans des considérations de fonctions complexes.
A+
Annuler
connectez vous