Inscription / Connexion Nouveau Sujet
ensemble de points
bonjour a tous si vous pouviez m'aider please mercii d'avance
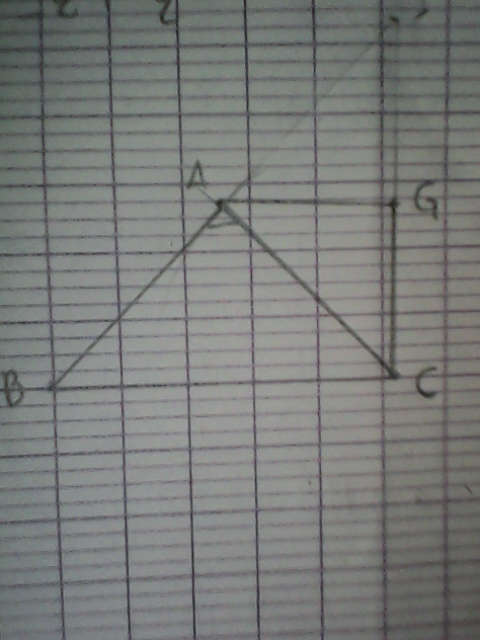
soit ABC un triangle rectangle isocele en A tel que AB=AC=3a avec a appartient [1,+[
a)determiner l'ensemble des points M du plan tels que
4MA2(au carre) -2MB2-2MC=-36a2
pour cette question j'ai resolu jusqu'a trouver MA*2AI=0 d'ou l'ensemble des points M du plan est une droite passant par A perpendiculaire a la direction du vecteur AI
b)||4MA -3MB+2MC||=||2MA-MB-MC||
la j'ai considerer G=bar {(A,4),(B,-3),(C,2)} et H {(A,2),(B,-1)(C,-1)}
et j'ai trouver 3MG=-2/3AI
c) 4MA2-2MB2+2MC2=-36a2
c'est la que je comprend pas j'ai introduit des point mais je vois pas
Bonjour Piwpamw.
Pour moi votre en énoncé comporte au moins une erreur :
4MA2(au carre) -2MB2-2MC=-36a2 soit 4MA² - 2MC² - 2MC = -36a2
En effet il y à trois longueurs à la puissance 2 (MA, MB et a) et une longueur à la puissance 1 (MC).
Le bon texte ne serait il pas :
4MA^2 -2MB^2-2MC² =-36a2 ?
Cordialement.
Phj69
bonjour a tous si vous pouviez m'aider please mercii d'avance
soit ABC un triangle rectangle isocele en A tel que AB=AC=3a avec a appartient [1,+[
a)determiner l'ensemble des points M du plan tels que
4MA2(au carre) -2MB2-2MC=-36a2
pour cette question j'ai resolu jusqu'a trouver MA*2AI=0 d'ou l'ensemble des points M du plan est une droite passant par A perpendiculaire a la direction du vecteur AI
b)||4MA -3MB+2MC||=||2MA-MB-MC||
la j'ai considerer G=bar {(A,4),(B,-3),(C,2)} et H {(A,2),(B,-1)(C,-1)}
et j'ai trouver 3MG=-2/3AI
c) 4MA2-2MB2+2MC2=-36a2
c'est la que je comprend pas j'ai introduit des point mais je vois pas
ce barycentre n'existe pas ...!
Matheuxmatou j'ai mi ||3MG||=||2MA+(-MA-AB)+(-MA-AC)||=2MA-MA-MA-AB-AC
=-(AB+AC)=-2*AI avec I milieu de[BC]
||2MA+(-MA-AB)+(-MA-AC)||=2MA-MA-MA-AB-AC
je vois mal comment tu peux avoir une norme (réel positif) égale à un vecteur !
et si tu ne sais pas utiliser le Latex (bouton en bas "aide au latex") tape v(AB) quand tu veux parler du vecteur , et AB quand c'est la distance
C vrai que je suis pas spécialiste en barycentre et pour le a?
ça n'a rien à voir avec la manipulation de barycentre... c'est que c'est incohérent... tu as une norme de vecteur qui est égale au vecteur ... ça n'a aucun sens
Bonjour Piwpamw.
Question a :
Soit M(x,y) on peut calculer
MA^2=x^2+y²
MB^2=x² = (3a-y)²
MC^2= (3a+x)^2 + y^2
4MA^2 -2MB^2-2MC² =-36a2 devient
4[x^2+y²] -2[x² = (3a-y)²] -2[(3a+x)^2 + y^2]= -36a
Au bout du compte on a y=x, donc M appartient à la médiatrice de BC.
Cordialement.
Phj69
Oui Mathieu c ce que j'ai mis c'est juste que je ne comprend pas comment mettre les signes...mercii encore
@ phj69
faudrait définir un repère si tu veux passer aux coordonnées... et je ne crois pas que ce soit le but de l'exercice.
Oui Mathieu c ce que j'ai mis c'est juste que je ne comprend pas comment mettre les signes...mercii encore
mais ils sont bons tes signes et tes manipulation de vecteur... ce qui est faux c'est que tu confonds norme et vecteur !
tu arrive à la même chose que moi à 16:37 si tu ne perds pas les normes en route
Phj69 pourriez vous m'expliquer je comprends pas ce que vous avez fait ...ce que j'ai fais c'est faux donc?
et pour :
c)4MA2-2MB2+2MC2=-36a2
décompose tout en passant par le point H barycentre de (A;4)(B;-2)(C;2)
@Piwpamw
reste sur la méthode que tu as amorcée et oublie les coordonnées pour l'instant...
ce que tu as fait au (a) est juste
Bonjour Piwpamw.
Question a :
Soit M(x,y) on peut calculer
MA^2=x^2+y²
MB^2=x² = (3a-y)²
MC^2= (3a+x)^2 + y^2
4MA^2 -2MB^2-2MC² =-36a2 devient
4[x^2+y²] -2[x² = (3a-y)²] -2[(3a+x)^2 + y^2]= -36a
Au bout du compte on a y=x, donc M appartient à la médiatrice de BC.
Cordialement.
Phj69
cela est totalement faux... 3a est la distance AB, pas l'ordonnée de B
D'accord ...j'ai trouver 4MH^2+4HA^2-2HB^2+2HC^2=-36a^2
bien
reste à calculer AH² ; BH² et CH²
résultats incohérents et non homogènes... on ne peut avoir du "a" et du "a²"... c'est comme si on ajoutait des longueurs et des aires !
et si tu trouves AH = 0 ... c'est que H est en A ! c'est la cas ?