Inscription / Connexion Nouveau Sujet
Exerci 3eme difficile
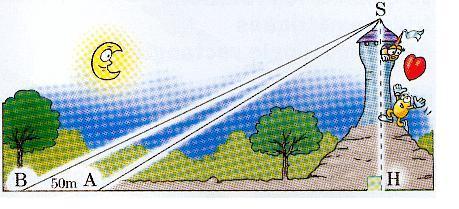
On veut déterminer la hauteur de la tour. Pour cela, on vise S d'un point A situé à une distance inconnue du pied de la colline. On effectue une deuxième visée en un point B situé à 50m de A, les points S, A et B étant dans un même plan vertical.
= 21° et = 18°
On pose SH = x.
1. Exprimer AH en fonction de x et de tan .
2. Exprimer BH en fonction de x et de tan
3.Exprimer AB en fonction de AH et AB et montrer que 50= x×tan -x× tan
4.calculer et
5.En déduire la valeur exacte de x
6.En déduire la hauteur de la tour en arrondissant votre résultat au m.
Il n'y a pas de question 4 desolé je me susi tromper
On veut déterminer la hauteur de la tour. Pour cela, on vise S d'un point A situé à une distance inconnue du pied de la colline. On effectue une deuxième visée en un point B situé à 50m de A, les points S, A et B étant dans un même plan vertical.
= 21° et = 17.8°
On pose SH = x.
1. Exprimer AH en fonction de x et de tan ASH
2. Exprimer BH en fonction de x et de tan BSH
3.Exprimer AB en fonction de AH et AB
5.En déduire la valeur exacte de x
6.En déduire la hauteur de la tour en arrondissant votre résultat au m.
bonjour,
tanx=côtéopposé/côté adjacent
1) triangle SAH rect en H
tan 21°=.../...--> AH=...
2)triangle SBH rect en H
tan 18°=.../...--> BH=...
3)AB=50=BH-AH=..........
à résoudre
tanx=côté opposé/côté adjacent
exemple dans SAH :
SAH=21°
SH=côté opposé=x
AH= côté adjacent
tan21°=x/AH
AH=x/tan21°
Pouvez-vous m'aider j'ai trouver pour tanASH=ah/hs
AH=tanASHxSH = ASH=tan 69= Ah/hs j'ai moi meme pas ocmpris ce que j'ai écrit je susi perdu réexpliqué moi dés le début
 :?
:? :?
:? :?
:?




