Inscription / Connexion Nouveau Sujet
Exercice 1/2 du DM de maths
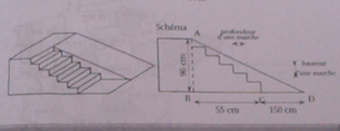
On souhaite construire une structure pour un skatepark consituée d'un escalier de six marche identiques
permettant d'accéder a un plan incliné dont la hauteur est égale à 96 cm. Le projet de cette structure est
présenté ci dessous.
-Normes de construction de l'escalier :
60 < 2h + p < 65 ou est la hauteur d"une marche et p la profondeur d'une marche, en cm.
-Demandes des habitués du skatepark :
Longeur du plan incliné (c'est-à-dire la longeur AD) comprise entre 2.20m et 2.50m
Angle formé par le plan incliné avec le sol (ici l'angle BDA) comprise entre 20° et 30°
1) Les normes de construction de l'escalier sont-elles respectées?
2) Les demandes des habitués du skatepark sont-elles satisfaites.
Bonjour j'arrive pas à faire cette exercice je doit le rendre pour lundi Merci ! 
Bonjour,
comme le nombre de marches de la figure est exact (6) et pas "de principe" tu peux compter directement sur la figure combien de "hauteur de marche" il y a dans les AB = 96 cm de haut et donc calculer la hauteur h d'une marche
pareil pour la profondeur p (largeur) d'une marche, à partit du nombre de marches sur BC
puis calculer 2h+p et donc répondre à la question 1.
pour la question 2, calculer (c'est un bien grand mot  ) la mesure de BD.
) la mesure de BD.
et donc la longueur de l'hypoténuse AD (Pythagore)
puis (trigo à réviser) l'angle ABD
Donc l'hauteur d'une marche = 96/6 = 16 Donc 1 marche = 16cm.
La largeur d'une marche = 55/6 = environ 9.16
2x16+9.16 =41.6
Donc les normes des escaliers ne sont par respecter.
Pour la question 2: 55+150 = 205cm.
Mais pour le reste il faut dire que le triangle est rectangle mais je ne me rapelle plus trop ^^
Ou sinon Merci ! 
compte attentivement combien de "largeurs" il y a ...
moi je n'en compte pas 6.
mais je ne me rapelle plus trop
(et ça sera mieux mémorisé si tu fais l'effort de le chercher dans ton cours et de le reviser que si on te le donne "tout cuit")
Pythagore et trigo dans un triangle rectangle, c'est à connaitre par coeur
(le triangle est rectangle "par hypothèse" : parce qu'une verticale et une horizontale sont perpendiculaires "par définition")
Ah oui désoler, il y'a 5 Longeurs Donc c'est 55/55 Donc 11cm chacuns
Du coup 2x16+11 = 43cm Donc ce n'est toujours pas respecter.
J'ai chercher mais je trouve toujours pas comment prouvez que c'est rectangle avec 2 mesures ^^
OK pour la 1.
Q2 : ????????
tu n'as pas à prouver qu'il est rectangle !!!
il est rectangle PAR DEFINITION
parce que toute verticale (AB) est forcément perpendiculaire à une horizontale (BD), c'est la définition même
(la distance "verticale" AB est ... verticale, par définition !!)
et donc SACHANT qu'il est rectangle tu dois juste appliquer Pythagore et la trigo pour répondre aux question posées et pas à d'autres :
mesure de AD
mesure de l'angle
Donc on sait que le triangle est rectangle alors
AD² = AB² + BD²
AD² = 96² + 205²
AD² = 9216 + 42025
AD = √51241
AD = environ 226.36cm
Donc 2.26m
On sait que le triangle est rectangle donc
COS 205/226 = ARCOOS(205/226) = 24.89 donc 24.9°
On sait que 2.26m est compris entre 2.20m et 2.50m et que 24.9° est compris entre 20° et 30°
Mais malheureusement la demandes des habitués du skatepark ne sont pas satifaisantes car elle ne sont pas
dans les normes de construction de l'escalier
Tu peut me dire si c'est juste ou sinon merci beaucoup pour ton aide ! 
c'est numériquement juste, mais la rédaction est aussi loufoque que d'écrire 1 = 2
COS 205/226 non.
cos(BDA) = BD/AD = 205/226 il n'y a aucun "cos 205/226"
ARCOOS(205/226) = 24.89 non
donc BDA = arccos(205/226) ...
l'angle BDA n'est pas un cosinus, c'est deux lignes séparées sans "=" entre les deux
ecrire que cosinus arcos c'est écrire que 1 = 2 (que 205/226 = 24.89)
ecrire cos 205/226 c'est confondre un angle et son cosinus.
enfin la phrase de conclusion n'est pas en accord avec ce qui est textuellement demandé dans l'énoncé
2) Les demandes des habitués du skatepark sont-elles satisfaites.
les demandes c'est juste et uniquement :
-Demandes des habitués du skatepark :
Longeur du plan incliné (c'est-à-dire la longeur AD) comprise entre 2.20m et 2.50m
Angle formé par le plan incliné avec le sol (ici l'angle BDA) comprise entre 20° et 30°
Ces demandes là sont bien satisfaites.
Que le constructeur de l'escalier (question 1) refuse de leur fabriquer cet escalier est une autre histoire qui n'a rien à faire dans cette question 2.
toi tu rajoutes une question 3 : les habitués du skatepark auront-ils leur structure telle qu'ils la demande et aux normes
et effectivement la réponse à cette question là sera non.



