Inscription / Connexion Nouveau Sujet
exercice
bonjour j'ai cet exercice mais je n'arrive pas a demontrer
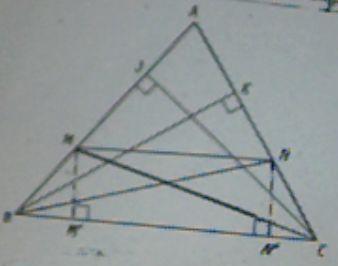
demonstration d'euclide du theoreme de thales dans un triangle
la droite (MN) est parallele a la droite (BC)
1) a justifier que les triangles BMC et BNC ont la meme aire c'est a dire : A(BMC)= A(BNC)
j'ai dit : A(BMC) = A (BNC) puisque ces deux triangles ont ici la meme base [BC] ET DES HAUTEURS IDENTIQUES mm' et NN'
b en deduire que A(AMC) = A(ANB)
2)a demontrer que A(AMC)/ A(ABC) = AM/AB
b demontrer que A(ANC)/ A(ABC) = AN/AC mais la ils ont du se tromper dans l'enonce ca peut pas etre A(ANC) ce serait plutot ANB
3) deduire des questions precedentes que AM/AB = AN/A
tu devrais écrire CJ pour les deux expressions (plutot que de mettre h à la 2eme).
Donc maintenant si tu divises ces 2 expressions tu vas pouvoir simplifier plein de choses, et il ne restera que ce que l'on te demandait 
La 1)a. tu y as déjà répondu (tu donnes la réponse dans ton premier message), pour la b) tu peux remarquer que:
(et pareil avec l'autre triangle)


