Inscription / Connexion Nouveau Sujet
Exercice : Application du produit scalaire (Theorème d'Al-Kashi)
Bonjour,
Je ne parviens par à résoudre un exercice dont voici l'énoncé :
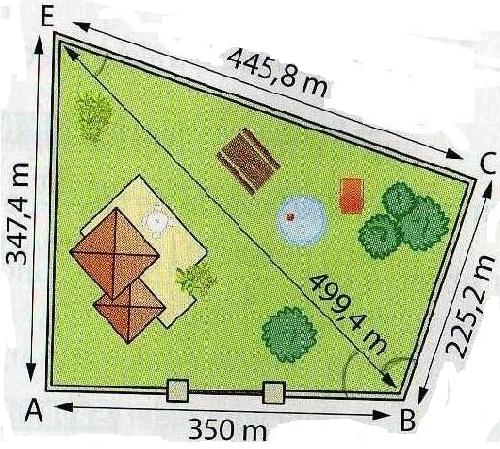
Un propriétaire souhaite mesurer la distance entre deux extrémités opposées de son terrain (AC sur la figure), malheureusement, sa maison l'empêche d'effectuer cette mesure.
1)A l'aide des mesures connues, calculer la longueur AC.
J'ai essayé d'utiliser le théorème d'Al-Kashi dans ABC mais il me manque la mesure de l'angle B.
J'ai ensuite essayé de trouver la mesure de l'angle ABE et EBC pour les additionner et en déduire la mesure de l'angle B mais j'obtiens une mesure approximative en degrès qui risque de fausser le résultat final.
Y a t-il un moyen plus exact pour résoudre cet exercice ?
Al-Kashi dans ABE --> angle ABE
Al-Kashi dans BCE --> angle EBC
puis angle B = ABE + EBC
puis Al-Kashi dans ABC --> longueur AC
utilise Al-Kashi pour trouver la mesure de l'angle B1 dans le triangle BEC
Fais de même avec le triangle ABE pour obtenir B2
Tu auras l'angle B
Chauchy77 : Aucune autre information n'est présente dans l'énoncé.
GGenn et pgeod : C'est ce que j'ai fait mais je doute de la précision du résultat. Existe t-il un autre moyen ?
bonsoir,
je ne saisis pas bien ton problème de précision: avec une calculatrice moderne tu peux calculer un arccos (ou un arcsin) sans souci particulier de précision.
si les degrés t'ennuient, utilise les radians.
Une mesure à deux chiffres après la virgule suffit ?
J'ai oublié comment convertir en radian.s.
Ici l'angle B mesure 107.16°.
Pas d'autres moyens.
Les valeurs d'angles sont à exprimer avec suffisamment de décimales.
La valeur de la longueur recherchée l'est au dm près pour des distances de l'ordre de 500 m.
Donc en conservant des angles en degrés décimaux avec seulement 3 décimales,
ça va le faire.
Pour te contrôler, tu fais le même calcul en travaillant dans
le triangle ACE et en déterminant cette fois l'angle E.
pourquoi convertir?
tu demandes à ta calculatrice l'angle en radians ! c'est plus simple 
personne ne te demande d'utiliser les degrés.
d'autre part les calculs intermédiaires n'ont pas à être arrondis.
on te demande une longueur (là tu dois faire attention aux chiffres significatifs, surtout en physique)
mais tous les angles et les autres longueurs intermédiaires calculés ne doivent pas être tronqués durant les calculs.
(tu peux les tronquer si tu les indiques sur ta copie, mais pas dans les calculs)


