Inscription / Connexion Nouveau Sujet
Exercice Produit Scalaire 1ere S
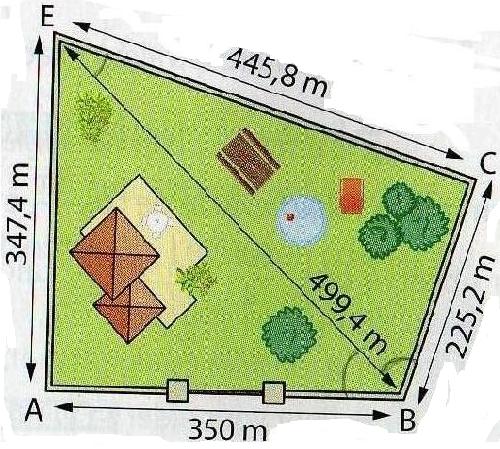
Bonjour , je suis actuellement bloqué sur un exercice sur le produit scalaire , Voici le schéma avec les données ci dessous .
J'ai réussi la première partie ou on me demande de calculer AC grace au théorème d'Al-Kashi .
J'ai trouvé AC = 469.02 m et L'angle B = 107.26°
Seulement j'arrive pas a trouver le bon calcul pour la seconde partie :
Le propriètaire a vu sur le cadastre que son terrain avait une aire de 1110 m² . Vérifier si cette valeur correspond aux mesures qu'il a effectuées .
On me dit en Aide : Utiliser le résultat démontré dans la partie précèdante ; l'aire d'un triangle ABC est : S = 1/2 AB*AC*Sin A = 1/2 BC*BA*Sin B = 1/2 CA*CB*Sin C
J'ai donc penser qu'il fallait utiliser cet formule dans les triangle ABC et AEC et j'ai choisis la formule suivante pour ABC : 1/2 BC*BA*Sin B
Seulement je trouve un résultat trop élevée : 37635.29572
Merci
Bonsoir,
A=350*347,4/2+1/2*445,8*225,2*sin (arccos(493,139^2-445,8^2-225,2^2)/(-2*445,8*225,2))=...m^2
ABE=arcsin(347,4/racine(350^2+347,4^2))
AEB=arcsin(350/racine(350^2+347,4^2))
493,139
493,139^2=445,8^2+225,2^2-2.445,8*225,2.cosC
Atriangle ECB=1/2*445,8*225,2*sin (arccos(493,139^2-445,8^2-225,2^2)/(-2*445,8*225,2))
Annuler
connectez vous