Inscription / Connexion Nouveau Sujet
Exercice, Produit scalaire
Bonjour, j'ai un exercice à faire et je bloque sur un calcul.
Je dois exprimer vecteur AE scalaire vecteur FB de deux manières différentes.
Et lorsque je le calcule avec le projeté orthogonal, je ne trouve pas le même résultat qu'avec la formule u.v = (1/2)(-|u|² - |v|² + |u+v|²) (tous ça en vecteur)
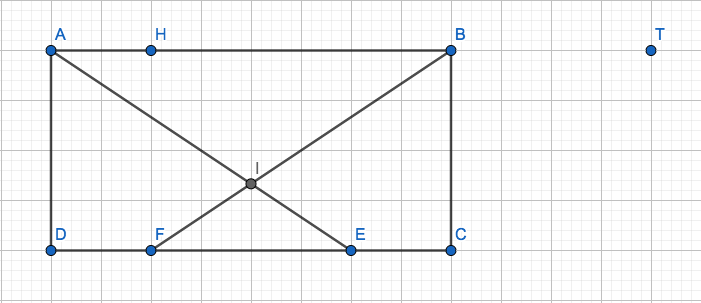
voici l'énoncé de mon exercice et la figure en pièce jointe : ABCD est un rectangle de sens indirect tel qu'indiqué sur le schéma ci-contre (qui n'est pas en taille réelle) tel que AD = 2 et DC = 4 E et F sont des points du segment DC tels que DF=EC=1 On appelle I l'intersection des droites (AE) et (BF) et AE=racine de 13.
Les points T et H n'étaient pas présents sur la figure d'origine, c'est moi qui les ai crées.
J'ai donc trouvé cela pour calculer AE.FB :
-Avec le projeté orthogonal :
je crée un point H tel que AH= 1 et H ∈ [AB]
AE.FB=AE.(FC.CB)
=AE.FC+AE.CB
=DE.FC+HB.CB
=9+0=9
- Avec la formule :
Je crée un point T tel que T ∈ (AB]) , BT=2 et AT=6
AE.FB=(1/2)(-|AE|² - |FB|² + |AE+FB|²)
=(1/2)(-26+|AT|²)
=(1/2)(-26+36)
=5
Puisque je ne trouve pas le même résultat, j'ai dû faire une erreur quelque part, mais je ne vois vraiment pas où est ce que je l'ai faite.
Aidez-moi s'il vous plaît, merci beaucoup 
La question entière est : En exprimant AE.FB de deux manières différentes, déterminer la valeur exacte de cos (EIB) puis une valeur approchée de l'angle EIB à 0,01 ̊près.
J'ai trouvé
AE.FB = AE*FB*cos(EIB)
5 = racine de 13 *racine de 13 * cos (EIB)
cos(EIB)=5/13
et
arccos (EIB) =67,38°
Est-ce correct ?
Bonjpur,
je pense qu'il faudrait supprimer complètement ces histoires de projetés orthogonaux pour les calculs des produits scalaires
vu que bon nombre d'élèves le comprennent de travers (un autre demandeur = même erreur et répétée plusieurs fois en plus) et projettent n'importe quoi sur n'importe quoi
alors que c'est uniquement le projeté d'un des vecteurs sur la droite support de l'autre et aucune autre droite !!
en remplaçant AE.CB
par HB.CB on aurait projeté AE sur la droite (AB) qui n'est pas le support du vecteur CB
correct est de projeter AE sur le support (BC) de CB, donc en BC.CB
ce n'est pas pas une histoire de "ne pas y penser" mais une histoire d'erreur de raisonnement à la base... (projeter AE sur n'importe quoi)


