Inscription / Connexion Nouveau Sujet
Exercice suites
Bonjour, j'aimerai obtenir de l'aide sur cet exo.
Un employeur envisage de proposer deux plans de rémunération mensuelle à un nouveau salarié à son embauche en janvier 2020.
Le salaire sera de 1900 € au départ avec deux options possibles :
-A : chaque année, une augmentation de 60 €.
-B : chaque année, une augmentation de 2.5 %.
1) On définit, la suite ( Un) de premier terme U0 = 1900 correspondant à l'option A et noté Un le salaire à l'année 2020 + n
a) donner les cinq premiers termes de la suite
b) exprimer Un+1 en fonction de Un en justifiant
c) exprimer Un en fonction de n en jsutifiant
2) Même questions avec cette fois ci une suite Vn pour l'option B Un employeur envisage de proposer deux plans de rémunération mensuelle à un nouveau salarié à son embauche en janvier 2020.
Le salaire sera de 1900 € au départ avec deux options possibles :
-A : chaque année, une augmentation de 60 €.
-B : chaque année, une augmentation de 2.5 %.
1) On définit, la suite ( Un) de premier terme U0 = 1900 correspondant à l'option A et noté Un le salaire à l'année 2020 + n
a) donner les cinq premiers termes de la suite
b) exprimer Un+1 en fonction de Un en justifiant
c) exprimer Un en fonction de n en jsutifiant
2) Même questions avec cette fois ci une suite Vn pour l'option B
3) Quelle est l'option la plus intéressante au bout de 10 ans ?
Alors pour la a) j'ai fais U2 = U0+60 = 1900+60 = 1960 puis U2 = U1+60 et ainsi de suite jusqu'à U5. Je ne sais pas si cette formulation est bonne.
et pour les deux autres questions je ne sais pas comment m'y prendre.
Je propose Un+1 = n+60 pour la 1b) et Un+1= n+2.5/100 pour la 2b).
Bonsoir
Qu'avez-vous écrit pour ? Que c'était le précédent
faites de même le précédent de
Que pouvez-vous en déduire ? nature de la suite
terme général
Je ne comprends pas ce que voulez vous dire dans le précédent de Un+1, je n'ai fais aucun calcul pour la b.
Et c'est une suite arithmétique où la raison est 60
question 1 b le précédent de est
.
Pour obtenir vous ajoutez à
, 60. c'est bien ce que vous avez fait pour obtenir
à partir de
.
on en déduit que
est une suite arithmétique de raison 60
Ce n'est pas ce que vous avez dans votre cours pour le terme général d'une suite arithmétique
Il est d'ailleurs surprenant que le premier terme n'apparaisse pas
He bien le premier terme est 1900? et la formulation que je vous ai proposé dans la c n'est pas bonne ?
C'est une suite arithmétique je vous avais écrit
Cela devrait vous permettre de retrouver la relation
D'accord. Je viens de remarquer que j'ai mis le sujet en double j'en suis désolé.
Du coup la 2)a) ce serait U1= U0+2.5/100= 1900+2.5/100= 1900.025 ?
Ca me parait bizarre comme résultat
Si cela vous ennuies pas, nous pouvons reprendre demain ? Car j'ai peur de vous déranger aussi tard. C'est déjà aimable à vous de m'aider
Le pourcentage est appliqué à quelque chose
Si on a une évolution au taux alors le coefficient multiplicateur est
un article de 100 euros en soldes à 20 % ne coûte pas 100-0,20 mais c'est-à-dire 80
ou si vous préférez 1 kg de farine 10% de farine en plus cela ne vous donne pas 1,010 mais 1+0,1 soit 1,1
À demain après-midi
Non le salaire n'est pas de 100 euros le pourcentage s'applique sur le salaire pas sur 100 pris pour des calculs rapides
Avant de continuer pour le 2), je voudrais votre validation pour cette partie ?
* Modération > Image effacée. Merci d'utiliser les outils mis à ta disposition pour écrire les formules mathématiques  *
*
1)a) U1=U0+60=1900+60=1960
U2=1960+60+2020
U3=2080
U4=2140
U5=2200
b) Un+1=Un+60. On en déduit que la suite (Un) est une suite arithmétique de raison 60.
c) Le terme général d'une suite arithmétique de 1er terme U0 et de raison r est Un=U0+nr
Par conséquent, Un=1900+60n.
Pourquoi des comportements différents
Si, dans , vous faites
ou 3 cela m'étonnerait que vous trouviez ce que vous avez écrit. Que vient faire l'année ici ?
La question c est correcte
en a) on vous demande les cinq premiers termes
en b) cela était correct. Elle permet d'affirmer que la suite est arithmétique
en c) le terme général en fonction de
Donnez les cinq premiers termes le seul correct était
en b) u_{n+1}=u_n+60, cela était correct. Elle permet d'affirmer que la suite est arithmétique
La question c est correcte
Très bien, passons au 2 si vous le voulez bien.
C'est le même concept mais avec une augmentation en pourcentage
Donc pour calculer U1, j'ai fais U1= 1900*2.5/100=47.5 Et donc 1900+47.5=1947.5. Est-ce cela ou une autre formulation
C'est cela, mais à la longue c'est pénible
Il vaut donc mieux passer par le coefficient multiplicateur . Icelui est 1,025 pour une hausse de
Donc je fais n*1.025, pour les 5 premiers termes.
Ensuite la b) serait Vn+1=Vn*2.5/100 ou Vn*1.025
C'est une suite géométrique de raison 2.5/100 ou 1.025
et la c) Vn=1900*2.5/100n ?
Il faudrait choisir
Vous avez bien vu que pour passer de à
vous avez multiplié par 1,025
donc on passe d'un terme au suivant en multipliant par
c) non ce n'est certainement pas cela que vous avez dans le cours. Il serait bien avant de faire un exercice de connaître le cours
Bonjour,
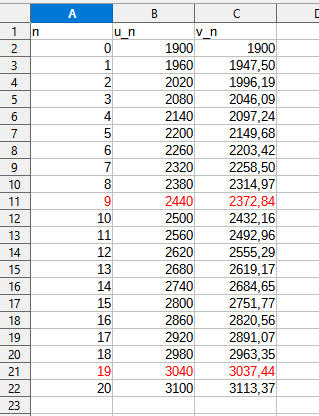
V9= 2372.8 et U9= 2440 (U9=1900+60*9 et V9=1900*1.0259).
On en déduit que l'option A est la plus intéressante au bout de 10 ans
4) V20=3113.4 et U20=3100
A partir de la 20ième année, l'option B devient plus intéressante.