Salut,

Par définition d'une fonction strictement croissante, celle-ci ne peut être périodique (un raisonnement par l'absurde devrait faire l'affaire).
Donc les fonctions de R dans R qui sont à la fois croissantes et périodiques sont les fonctions constantes...

bonjour : )

Mouchki penserait-il par exemple à ce qui suit en disant "parce que on peut avoir une fonction croissante discontinue et alors périodique" ?

f(x) = tan(x) avec I = R - {Pi/2 + k.Pi} (k dans Z)

Mais f n'est pas alors une fonction de R dans R.

@J-P
Que prouve l'exemple de la fonction tangente ?

@ alb12

Je n'essaie pas de prouver quoi que ce soit.
J'essaie juste de comprendre ce qu'a voulu dire Mouchki par son "parce que on peut avoir une fonction croissante discontinue et alors périodique"

Or, il me semble bien que avec f(x) = tan(x) avec I = R - {Pi/2 + k.Pi} (k dans Z), on a f est discontinue mais est croissante dans I (qui n'est pas connexe) et f est bel et bien Pi périodique.

Non ?

Mais, comme je l'ai noté, f n'existe pas alors partout dans R.

J'aurai du écrire :  "f est n'est pas continue dans R" au lieu de" f est discontinue ..."

--> J-P :

Peut-être plutôt f(x) = x - E(x) ?

Il n'existe de pas de fonction de discontinue qui soit croissante et périodique.

Mais oui on peut très bien imaginer l'erreur que Mouchki a faite.

La fonction tangente n'est pas croissante sur .

il me semblait que J-P affirmait que tan est croissante sur son ensemble de definition.
Probablement une erreur de ma part.

A nouveau, la fonction tangente n'est pas croissante sur , ceci, par définition même d'une fonction croissante.

En effet, alors que .

La restriction de la fonction tangente à un des intervalles avec , i.e. une des composantes connexes de , est en revanche croissante et même bijective de cet intervalle .

Je ne vois pas en quoi préciser que n'est pas connexe est utile.

Lire :
La restriction de la fonction tangente à un des intervalles avec , i.e. une des composantes connexes de , est en revanche croissante et même bijective de cet intervalle sur .

@J-P
Je te dis que tan n'est pas croissante sur son domaine de definition.
Tu me réponds: tu peux me dire là où elle serait décroissante ?
Ta conception de la negation est etonnante !

@mdr_non
bonne chance avec J-P c'est un specialiste ...

Et si au lieu de faire ton malin comme d'habitude, on attendait ce que Mouchki pensait avec son "parce que on peut avoir une fonction croissante discontinue et alors périodique  " ?

Juste pour savoir.

La fonction tangente est croissante dans chaque intervalle connexe où la fonction existe.

Et bien entendu, ce n'est pas vrai en considérant des valeurs de la variable prises dans des intervalles non connexes.

Bien entendu

salut

soit f une fonction croissante et périodique de période t

soit x un réel tel que f(x), f(x + t/2) et f(x + t) existent  (ouf!!)

f est périodique donc f(x + t) = f(x) (1)

f est croissante donc f(x) f(x + t/2) (2)

(1) + (2) => f(x + t) f(x + t/2)


donc f est constante ...


de toute façon par définition (de croissance et décroissance) ça n'a pas de sens de parler d'une fonction (dé)croissante sur un ensemble non connexe : ex classique : la fonction inverse ...

Ne suffit-il pas que les ensembles de depart et d'arrivee soient ordonnes pour parler de ces notions ?

Attendons l'avis d'un specialiste.

Il n'y a aucun problème de définition.

On peut parler de la monotonie d'une fonction définie sur , avec une partie quelconque de , en particulier (e.g. les suites numériques).

carpediem a voulu dire autre chose.
Par exemple, lorsqu'on caractérise des fonctions monotones grâce à la notion de dérivabilité, les théorèmes sont faux si la partie de considérée n'est pas un intervalle.

E.g. : Si est un INTERVALLE, et une fonction dérivable sur , alors est constante sur ssi est nulle sur .
Ce théorème est faux si est une réunion d'intervalles disjoints.

Dans mon précédent message je considère bien évidemment à valeurs réelles.

Plus généralement et pour répondre à alb12 qui de toute façon connaissait la réponse,
Si et sont deux ensembles ordonnés, et , on définit très bien la monotonie de .

est croissante si .
etc.

"carpediem a voulu dire autre chose. "

Ah bon ????

Trouvé ici :




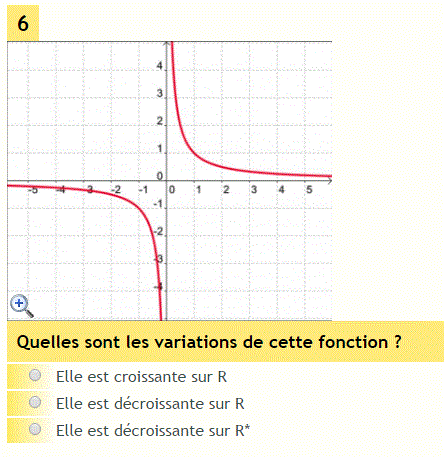
Il faut choisir la bonne solution dans les 3 proposées.

Je ne cautionne ni ne réfute ce qui précède, je me contente de pointer que tous n'ont pas la même opinion sur le sujet et que tous n'utilisent visiblement pas les mêmes définitions.

Comme si ce n'était pas évident.
Même si chacun pense que ce sont les définitions qu'il utilise les correctes et aucune autre.

Je rejoins carpediem (une fois n'est pas coutume) dans ses propos.

Et recopie donc ce que j'ai déjà écrit :

Tous n'ont pas la même opinion sur le sujet et tous n'utilisent visiblement pas les mêmes définitions.

Comme si ce n'était pas évident.
Même si chacun pense que ce sont les définitions qu'il utilise les correctes et aucune autre.

chacun jugera les references de J-P. Ridicule.
mdr_non a donne la definition.
Celle qui permet de montrer aux lyceens que la fonction inverse
n'est pas monotone sur son ensemble de definition.
Et d'insister sur l'importance de travailler sur des intervalles
quand on utilise le signe de la derivee.

Trouvé sur internet....(un site sérieux je vous l'assure....)


conclusion : il y a plusieurs règles d'accord appliquées par les enseignants de Français

ouais enfin dans ce cas on peut penser à "une bête erreur classique" ou faute d'inattention ...

par contre il est évident que le site que présente J-P est peu recommandable pour faire des math ...


ensuite il est clair que tout le monde s'accorde sur la définition de mdr_non ... mais qui montre toutes ses limites dans le cas d'ensemble non connexe voir mon post et ne permet pas de dégager des propriétés d'une fonction)

maintenant dans le cadre de l'apprentissage

1/ il y a une définition précise en seconde (qui n'est absolument pas contradictoire avec celle de mdr_non)

f est croissante sur l'intervalle I : pour tout réels u et v de I : u < v => f(u) f(v)

ce qui suppose implicitement que :

I est connexe
f est définie sur l'intervalle I

ce qui permet de dégager réellement ces définitions de variations (et permet de poursuivre en mathématiques sans désaccord avec des définitions plus généralistes)

Complément à mon message précédent.

Et pareil pour les mathématiques... évidemment

ce n'est pas le seul cas où une definition de lycee est modifiee apres le bac.
ce qui ne signifie pas que les enseignants ne sont pas d'accord.

carpediem,

J'ai l'impression que tu n'as pas lu mon message.

Citation :
1/ il y a une définition précise en seconde (qui n'est absolument pas contradictoire avec celle de mdr_non)

f est croissante sur l'intervalle I : pour tout réels u et v de I : u < v => f(u) f(v)

ce qui suppose implicitement que :

I est connexe
f est définie sur l'intervalle I

mdr_non @ 04-07-2016 à 12:19

Il n'y a aucun problème de définition.

On peut parler de la monotonie d'une fonction définie sur , avec une partie quelconque de , en particulier (e.g. les suites numériques).

Bonjour
en gros, pour éviter que les élèves de lycée n'écrivent des sottises du genre "la fonction inverse est décroissante sur ]-oo, 0[ U]0;+oo[", au lieu de "la fonction inverse est décroissante sur ]-oo, 0[ et sur]0;+oo[", on ne leur définit plus les variations que sur un intervalle ?
Sinon, si JP admet comme règle nouvelle d'orthographe toutes les fautes qui émaillent livres (y compris scolaires de français, hélas, bouclés dans la précipitation pour cause de réforme précipitée) et sites internet, sé plu la péne de sembété a écrir corekteman !

Le seul endroit où j'avais limité à un intervalle c'est bien à la fin de ce même message où je parlais du théorème qui caractérise les fonctions dérivables monotones.
Mais sinon, dans les définitions de fonctions monotones, est une partie quelconque de .

Soient une partie de et .

est croissante si .


Et ensuite dans le deuxième message j'ai parlé plus général encore en parlant d'ensembles ordonnés, ce qui permet alors de dire que par exemple la fonction : est croissante.

mon intervention faisait référence aux programmes de seconde, où apparemment on ne définit que sur un intervalle les notions de fonction croissante ou décroissante

mdr_non : je ne sais si tu es prof ... mais un apprentissage est progressif (quand on apprend à additionner on n'apprend pas ce qu'est un groupe additif !!!)

on découvre et on apprend des objets et des définitions précises ... qui permettent de travailler !!! (plus exactement que nos élèves puissent travailler !!!)

donc pour être plus explicite : ta (qui est la définition d'une fonction monotone sur deux ensembles ordonnés (notion qui n'est pas enseignée au lycée d'ailleurs)) n'a aucun intérêt au lycée car elle conduit par exemple à ce que relève lafol et conduit à de graves erreurs didactiques et pédagogiques ...

ensuite au fur et à mesure que les connaissances s'accumulent on peut effectivement faire évoluer les définitions pour les généraliser ou les donner dans un cadre plus formel ou général ... à celui qui les comprend et les digère ... comme le relève alb12


ça me gène de parler de fonction dérivable sans parler de fonction continue, de parler de loi binomiale ou autre sans même définir ce qu'est une variable aléatoire (de façon formelle dans une certaine mesure ^{de proba !!!}) ... mais je suis fonctionnaire donc :

1/ je fais ce qu'on me demande de faire ...
(2/ je compose avec ... dans une certaine mesure !!)
3/ je me satisfais de voir des élèves répondre (un peu) )à la philosophie actuelle des math au lycée : savoir modéliser une situation, puis répondre à la question par un raisonnement (élémentaire) ou un calcul (souvent approché)


bien entendu ça me désole car ça ne prépare nullement les personnes "brillantes" (à qui il faudrait donner un os sérieux à ronger et qu'on pénalise au profit de la masse et c'est bien sur vrai dans toutes les disciplines) ... mais c'est la loi ...

on ne fais quasiment plus de math au lycée ... et il faut faire avec ... enfin sans !!!

Non je ne suis pas prof et c'est peut être la raison pour laquelle je ne suis pas clair dans mes propos.
J'avais l'impression d'avoir été clair mais j'ai bien parlé de deux définitions de fonctions monotones : une pour le lycée et une générale.

1) Pour une fonction réelle définie sur une partie quelconque de .
On peut effectivement imposer à cette partie d'être un intervalle (ce n'est qu'un cas particulier de partie de ). Mais ça ne dure pas tout le lycée puisque ça ne comprend alors même pas le cas des suites réelles.

Soient une partie de et .

est croissante si .


2) Pour une fonction définie et à valeurs dans des ensembles ordonnés.

Soient et deux ensembles ordonnés et .

est croissante si .

Celle-ci je ne l'avais écrite qu'en éco à la remarque d'alb12.

au lycee les fonctions sont evidemment definies sur des parties de R.
la monotonie en principe ne s'etudie que sur des intervalles.