Inscription / Connexion Nouveau Sujet
Fonctions etc
J'ai un devoir en maths a rendre lundi et je n'y arrive pas en fait le sujet c'est une plaque de carton rectangulaire qui mesure 10dm sur 8dm et pour faire une boite on a découpé des quatre petits carrés aux quatres coins du rectangle et les questions sont auxquels je suis arrivés sont:
Dans la partie 1
dans cette partie on decoupe des carrés de 2dm de côté)
1) dessiner à l'échelle 1/10 le patron de la boîte
2) représenter en perpective cavalière la boîte obtenue
3) calculer son volume en litre,puis,en cm3
Dans la partie 2: (on decoupe des carrés de 2,5 dm de côté)
1) calculer en litres, le volume de la nouvelle boîte obtenue.
2) par rapport à la boîte de la partie précédente,le volume a t il augmenter ou diminué?
3 exprimer cette variation de volume sous la forme d'un pourcentage
Partie 3 c'est a partir de là que j'y suis pas arrivé !!)
On appelle la x la longueur (en dm) des cotés des quatre carrés découpés.
1) donner sous forme d'encadrement toutes les valeurs possibles pour x
2) déterminer sous sa forme développée,la fonction V exprimant le volume de la boîte en fonction de x
3) retrouver le résultat de la partie 1 en calculer V(2) (détailler les étapes du calcul)
Partie 4 : on veut savoir quelle valeur de x le volume V(x) de la boîte est maximum.
1) dresser un tableau de valeurs de V(x) en fonction de x pour une quinzaine de valeurs régulièrement reparties.
2) on veut tracer la représentation graphique de la fonction V.
Sur une feuille de papier millimétré construire un repère orthogonal tel que:
- en abscisse,1 cm represente 0,5 dm
- en ordonné, 1 cm représente 5 dm3 ( je ferais le "2)" seule avec vos résultats)
3) déterminer par la lecture graphique la valeur de x pour laquelle le volume de la boîte semble maximum ( faire apparaître les pointillés sur le graphique)
4) a l'aide d'un outil de calcul (calculatrice ou tableur) déterminer avec le plus de précision possible la bleue de x pour laquelle le volume de la boîte est maximum
Merci beaucoup d'avance sachez que si vous répondez vous me sauvez la vie!! 😭😭😭
Bonjour,
Partie 3
1) L'encadrement de x (exprimé en décimètre dm) est le suivant 0 
x 4
4 vient de 8/2
2) La longueur de la boîte sera L(x)=10-2x, la largeur l(x)= 8-2x et la hauteur h(x) = x
Le volume de la boîte sera donc V(x) = L(x) * l(x) * h(x) = (10-2x) * (8-2x) * x
En développant on trouve V(x) = 4x3 - 36 x2 + 80x exprimé en dm3 si x en dm
On vérifie que pour x=0 et x=4, on a un volume V(x) nul
3) Pour x = 2 dm on a donc V(2) = 32 - 144 + 160 = 48 dm3 (soit 48 L ou 48*103 cm3): on vérifie que l'on a le même résultat qu'en partie 1)
Fais aussi la vérification avec x=2,5 dm de la Partie 2
Partie 4
1) J'utilise Excel pour cela avec un pas pour x de 0,25 dm
Voir image ci-dessous (excuses pour la difficulté de lisibilité)
2) A toi de faire
3) On voit que le maximum se trouve aux alentours de x = 1,5 dm
4) En prenant un pas pour x de 0,01 dm autour de 1,5, je trouve avec Excel que le maximum serait pour x = 1,47 dm et vaudrait alors 52,5137 dm3
On peut approfondir encore en prenant un pas pour x de 0,001 dm autour de 1,47
Sauf erreur de ma part
Bon courage
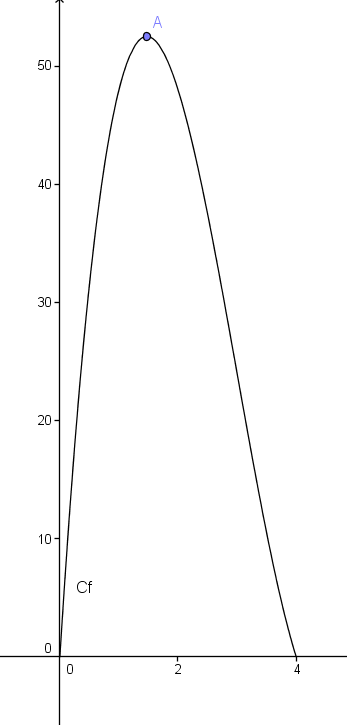
Voici la courbe de la fonction V(x) tracée sous Geogebra avec les échelles demandées
On retrouve que le point A pour lequel le volume est maximal a pour abscisse environ 1,47 dm
Tu apprendras plus tard qu'en étudiant la fonction dérivée appelée V'(x) de la fonction V(x), on peut déterminer les valeurs minimales et maximales de la fonction initiale (ici V(x)) qui sont telles que la fonction dérivée (ici V'(x)) est nulle
En faisant cela sous Excel, je trouve que xmax = 1,472474768 dm qui donne un volume Vmax = 52,51380432 dm3
Annuler
connectez vous