Inscription / Connexion Nouveau Sujet
géométrei dans l'espace ; sphère ; tangentes
Bonsoir à tous
voici un pb qui me paraît difficile. Pouvez-vs m'aider à le résoudre svp, merci.
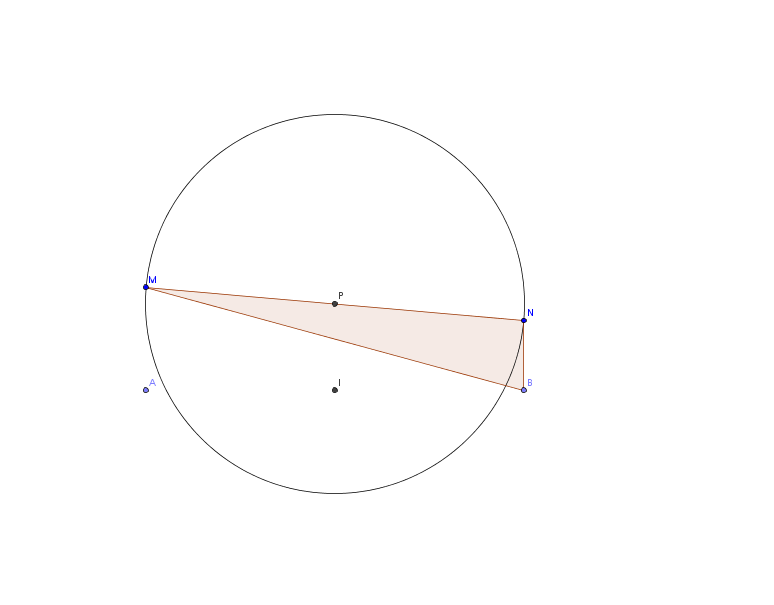
On considère, dans l'espace, un segment de droite [AB], de longueur 2a, de milieu I, et deux demi-droites [Ax) et [By), orthogonales, et dont le segment [AB] est la perpendiculaire commune.
On prend sur [Ax) un point variable M, et sur [By) un point variable N.
On pose AM = x ; BN = y.
1/ Evaluer, en fonction de a, x et y, la longueur d du segment [MN].
Prouver que les points A et B sont sur la sphère de diamètre MN.
2/ Trouver le lieu géométrique du point P, milieu de [MN] (c'est-à-dire l'ensemble des points P, milieux des segments [MN]) lorsque les points M et N varient dans les 4 cas ci-dessous :
a/ M est fixe et N décrit la demi-droite [By)
b/ M et N décrivent resp. [Ax) et [By), d'une manière arbitraire et indépendamment l'un de l'autre
c/ M et N décrivent resp. [Ax) et [By), le rapport restant constant
d/ MN reste égal àne constante donnée, arbitraire, supérieure à 2a.
3/ On se propose de trouver le lieu de P lorsque (MN) reste tangente à la sphère S de diamètre [AB].
a/ On suppose déterminée une tangente MN à la sphère S, et on appelle K le point de contact ; montrer que les triangles MIA et MIK d'une part, NIB et NIK d'autre part sont égaux.
En déduire une relation nécessairement vérifiée par x, y et a si (MN) est tangente à la sphère S.
b/ Montrer que pr M donné, il existe effectivement, ds le plan MBY, une droite (MN), et une seule, tangente à la sphère S.
En déduire qu'il est suffisant que x, y et a vérifient la relation trouvée au § a pour que (MN) soit tangente à la sphère S.
c/ Trouver le lieu géométrique du point P en déterminant son équation par rapport à deux axes convenablement choisis, resp. parallèles à [ax) et [By).
J'ai répondu à la 1ère question ainsi :
[AN] est l'hypoténuse du trg ABN, rectangle en B, dc :
[MN] est l'hypoténuse du trg MAN, rectangle en A, dc : .
C'est après que les difficultés commencent. Pouvez-vs m'aider à avancer svp.
D'avance merci.
1/ Si l'on coupe la sphère de diamètre MN par le plan NBM, l'intersection est un grand cercle de la sphère et B est sur ce grand cercle (pour bien le voir, tu peux faire une figure à plat du plan NBM). Même raisonnement pour A.
2/a Le plan NBM est fixe et tu peux encore raisonner sur ta figure à plat.
Bonsoir Priam
L'obtention d'un grand cercle de la sphère de diamètre [MN] qd on la coupe par le plan MNB, d'accord.
Ce que je ne comprends pas, c'est que A et B étant fixes, M et N variables, comment B et A peuvent-ils être nécessairement SUR la sphère de diamètre [MN]?
Ne faudrait-il pas prouver que A et B vérifient l'équation de la sphère dt on a déterminé le diamètre, en fixant une origine arbitraire , I par ex ? Si on peut écrire cette équation à partir des éléments dt on dispose ??
Je cherche ds ce sens là !
Oui, mais ce n'est pas nécessaire.
As-tu fait la figure à plat du plan MBy, avec le triangle MNB et le point P ?
Bonjour Priam, bonjour à tous
j'avoue que j'ai un peu de mal avec cette méthode.
Par contre, en supposant que l'espace est rapporté à un repère orthonormé d'origine A, j'ai réussi, en posant :
A : (0;0;0) ; B : (2a;0;0) ; M : (0;0;x) ; N : (2a;y;0) ;
à établir analytiquement que A et B appartiennent à la sphère de diamètre MN et de centre P.
J'ai aussi traité la question 2a. ma réponse est que ds ce cas, P aura tjs même abscisse et même cote, dc que le lieu cherché est une droite pasant par , et parallèle à [By).
Est-ce juste ?
merci de me dire
Q2b.
par un raisonnement similaire à celui que j'ai eu pr la Q2a, on a :
M : (0;0;x+ ) et N : (2a;y+
) et N : (2a;y+ ;0), (
;0), ( ;
; )
) [-x;+
[-x;+ [
[  [-y;+
[-y;+ [.
[.
P a dc pr coordonnées :
P aura tjs même abscisse a. Le lieu de P sera alors la plan comprenant I, et perpendiculaire au plan défini par (AB) et [By)
Est-ce juste ? merci de me dire
Bien que je ne sache pas ce que sont lambda et µ, je vois que ta conclusion est exacte : le lieu de P est le plan médiateur du segment AB.
Une remarque : tu appelles la cote du point M ..... x. Ce n'est pas dans les usages !
Bonjour Priam :
le plan médiateur, voilà, c'est le terme que je cherchais.
 et
et  sont les variations de mesure de AM et BN lorsque M et N varient en position sur leurs demi-droites resp., x et y étant des mesures initiales.
sont les variations de mesure de AM et BN lorsque M et N varient en position sur leurs demi-droites resp., x et y étant des mesures initiales.
tu appelles la cote du point M ..... x. Ce n'est pas dans les usages !
Excuse-moi, ça peut prêter à confusion, mais bon...tu arrives à me suivre, en + du tps que tu me consacres, tu es doublement méritant, merci

j'essaie de finir la Q2 ce soir, je pense avoir trouvé pr 2c, et j'ai commencé à réfléchir à 2d. Je posterai tt ensemble, avant d'attaquer la Q3 qui me paraît + difficile
Bonjour à tous, 
Je suis ton topic depuis le début pppa; Priam, que je salue, t' ayant répondu avant que je ne réagisse, je me suis bien gardé d' intervenir par la suite...
Juste quelques petits commentaires:
- On a et
; il aurait été logique de prendre pour repère
orthonormé direct où:
Dans ce repère, on a ce qui est tout de même plus pratique pour la suite.
- On nous parle au début de l' énoncé de demi droites et
Si bien que et
.
Et que les lieux de dans 2) et 3) sont des portions de droites, de plans, de courbes...
-Un prolongement possible de cet exercice:
Quel est le lieu de point de contact de la tangente
à la sphère ?

Bonsoir Cailloux, Bonsoir Priam
merci pr vos interventions.
Effectivement, mon choix de repère n'est pas judicieux.
Veux-tu que je reprenne l'exercice en me "basant" sur le repère que tu proposes ?
Sinon pr la Q2c j'ai trouvé : le lieu de P est la portion de droite incluse ds le plan mentionné à la Q2b, passant par I, de pente , en fait incluse je pense ds le quart de plan délimité par la demi-droite parallèle à [Ax) partant de I, et la demi-droite parallèle à [By) partant de I
Pr la Q2d, j'ai trouvé que le lieu de P est un segment de droite, inclus ds la même portion plan que celle mentionnée ci-dessus (q2c, valable pr la q2b aussi je pense ??)
qui joint :
- le milieu de [MN] lorque ce segment est inclus ds le plan défini par (AB) et [By), i.e qd M est confondu avec A
et
- le milieu de [MN] lorque ce segment est inclus ds le plan défini par (AB) et [Ax), i.e qd N est confondu avec B,
MN = d conservant la même mesure au fur et a mesure que M s'éloigne de A et que concomitament N se rapproche de B
Est-ce exact ?
Merci de me dire 
Bonjour pppa:
Je me place dans mon repère....
2)c) Oui, une demi droite issue de d' équation
avec
,
et
dans le repère
du plan d' équation
2)d) Je ne te suis pas bien:
On a donc
et (qui est bien positif puisque
)
et avec
et
Les coordonnées de vérifient donc:
appartient donc à l' intersection d' un "quart de cylindre" d' axe
(la première équation et les 2 dernières inéquations) et du plan d' équation
Il s' agit du cercle de centre et de rayon
du plan d' équation

Bonsoir Caillox
je comprends ce que globalement tu écris pr a Q2d ; la seule chose que je ne comprenne pas, cest prquoi les coordonées de P vérifent x²+y²+4a² = k² ; ce nombre est le carré de la distance MN, il mesure une distance. Certes P est le milieu de {MN], mais prquoi les coordonées de P doivent vérfier cette "équation" ? je ne comprends pas.
Merci de me dire
Bonjour pppa,
prquoi les coordonées de P vérifent x²+y²+4a² = k²
Je n' ai jamais écrit cela, regarde bien:
Effectivement
Dnas 2)d), D' une part, l' énoncé nous impose
Donc
et d' autre part (depuis le début de l' énoncé), les cooordonnées de
Ces coordonnées vérifient donc:
Autrement dit en posant
Autrement dit encore,
et il y a les autres conditions:

Bonjour Cailloux
merci pr tes éléments de réponse pr la Q2d. C'est compris.
ma réponse pr la Q3a.
Les triangles MIA et MIK ont le côté [MI] en commun.
[IA] et [IK] sont 2 rayons de S, dc IA = IK
[IA]  (AB) et [IB]
(AB) et [IB]  (AB)
(AB)
et
[AM)  (AB) et [BN)
(AB) et [BN)  (AB)
(AB)
dc
MIA trg rtg en A, d'hypoténuse [MI]
et
MIK trg rtg en K, d'hypoténuse [MI], puisque [MK]  (MN) et (MN) tg à S en K, dc perp. au rayon de S aboutissant en K, soit [IK].
(MN) et (MN) tg à S en K, dc perp. au rayon de S aboutissant en K, soit [IK].
De tt cela, il résulte en appliquant le tm de Pythagore :
MA² + IA² = MI² = MK² + IK² = MK² + IA²
On en déduit :
- MA = MK = x
- MIA et MIK sont deux trgs ayant leurs 3 côtés égaux chacun à chacun, , dc ces 2 trgs sont égaux.
Les triangles NIB et NIK ont le côté [NI] en commun.
[IB] et [IK] sont 2 rayons de S, dc IB = IK
[IB]  (AB) et
(AB) et
[BN)  (AB) dc
(AB) dc
NIB trg rtg en B, d'hypoténuse [NI]
et
NIK trg rtg en K, d'hypoténuse [NI], puisque [NK]  (MN) et (MN) tg à S en K, dc perp. au rayon de S aboutissant en K, soit [IK].
(MN) et (MN) tg à S en K, dc perp. au rayon de S aboutissant en K, soit [IK].
De tt cela, il résulte en appliquant le tm de Pythagore :
NB² + IB² = NI² = NK² + IK² = NK² + IB²
On en déduit :
- NB = NK = y
- NIB et NIK sont deux trgs ayant leurs 3 côtés égaux chacun à chacun, , dc ces 2 trgs sont égaux.
Par contre pr la relation entre a, x et y, j'ai réfléchi + d'un 1/4 h, je ne vois pas...qqc de remarquable; peux tu me mettre sur une piste stp ?
Q3b : sans grande conviction, et non achevé puisqu'il me manque la relation à trouver à la question précédente :
L'intersection de S et du plan (MBY) est soit, suivant le position de M :
- le demi-grand cercle ABK qd M est en A
- un secteur circulaire comprenant K
- le point K
- l'ensemble vide.
Je cherche à établir qu'il existe un point de tangence K du côté [MN] du trg MBN avec S, mais je n'arrive pas à établir que ce soit nécesasirement le cas.
Peux-tu me donner des pistes pr répondre à la question stp ?
Q3c : j'ai recopié l'énoncé in extenso ; je suppose qu'on cherce le lieu de P lorsque (MN) varie comme tangente à S. Comprends-tu comme moi ? Si oui,peux tu aussi me donner des pistes pr trouver la solution stp.
Merci d'avance.
Quelques réflexions pr essayer d'avancer (même si ça va pas me mener bien loin) d'abord parce que ça m'intéresse et aussi pr que tu n'aies pas l'impression que je me repose sur toi.
Je parle de la Q3b
pr un point M donné sur ]Ax), sauf à ce que m soit rejeté à l'infini sur ]Ax), (MB) coupera S en deux points distincts. en faisant varier N sur [BN), (M et B restant fixex), à partir de B, l'ensemble des points d'intersection de (MN) avec S comprendra tjs deux points, jusqu'à atteindre une position limite, fonction de l'emplacement de M sur [Ax) et du rayon a de S, position UNIQUE qui réduira l'ensemble des points d'intersection de (MN) avec S à un seul point K. Au-delà de cette position de N su [BN), l'ensemble des points d'intersection de (MN) avec S sera l'ensemble vide.
(MN) étant nécessairement incluse ds le plan (MBY), est-ce que cette analyse suffit pr répondre à la question ?
Bj Priam
Ah oui : 
On sait que (Q1) MN² = x² + y² + 4a²
J'ai établi ds la 1ère partie de la q3a les égalités des 2 trgs,d'où il résulte que
MN = x+y
Dc (x+y)² = x² + y² + 2xy = x² + y² + 4a²
soit 2xy = 4a² ou xy = 2a².
Dc on est en présence d'un produit de deux variables égales à une constante.
J'ai déjà vu ça qq part 
Est-ce que ça va m'aider à répondre à la Q3b 

merci Priam
il faut absolument que je sache reconnaître au 1er coup d'oeil ce type d'écriture ; je Pense que je m'en souviendrai maintenant
Dc x ne peut pas être nul, soit M ne peut pas être confondu avec A...
Quand x tend vers 0, M tend vers A et MN tend à être parallèle à l'axe By. Les points P et N sont rejetés à l'infini.
Résultat analogue si y tend vers 0.
Bj Priam
oui d'accord, puisqu'on considère une tg donnée à la sphère, j'ai compris
Maintenant, je ne comprends pas (encore) ds quelle mesure la détermination de cette hyperbole peut me permetre de répondre à la Q2b
merci de me dire
Pour répondre à la Q3b, je dirais ceci :
Du point M, on peut mener une infinité de tangentes à la sphère S, qui forment un cône de révolution ayant M pour sommet.
Le plan MBY coupe ce cône suivant deux génératrices, qui sont deux tangentes à S. Mais, comme les axes Ax et By sont limités à des demi-droites, il n'y en a qu'une qui soit utile le cadre du problème.
Réciproquement, si on a la relation xy = 2a², MN est tangent à S :
On sait que MN² = x² + y² + 4a², expression qui est égale à (x + y)² - 2xy + 4a².
Du fait de la relation ci-dessus, on a MN² = (x + y)², soit MN = x + y.
Or, x et y sont les longueurs de tangentes à S issues respectivement de M et de N.
MN, dont la longueur est égale à la somme de celles de ces deux tangentes, est donc composée de celles-ci et est tangente à S.
Cailloux, que je salue bien, évoquait le lieu du point de contact K de MN avec la sphère S.
C'est un grand cercle de celle-ci (ou plutôt un demi grand cercle) de diamètre AB, incliné de 45° par rapport à chacun des deux axes Ax et By.
Merci bcp Priam 
sur la preuve de l'unicité de la tg à S, j'ai compris (j'aurais jamais pensé au cône de révolution de sommet M).
Sur l'inclinaison du demi grand cercle à 45 °, j'avoue que j'ai pas trop compris pr l'instant, mais comme c'est complémentaire au sujet, je préfère, si vs êtes d'accord qu'on termine avec la Q3c.
Je reviendrai après sur ce point complémentaire.
Merci pr votre aide.
Priam, Cailloux
si vs pouviez m'aider à terminer cet exercice, je vs en serais reconnaissant.
Les axes convenablement choisis, je ne vois pas.
Le lieu de P, apparemment ce serait une droite ? (je réponds pas complètement au hasard, mais d'après un schéma).
Après je me demande comment utiliser le fait que la relation entre x et y et a nous donne l'équation d'une hyperbole ?
Merci de m'aider
Dans l'hypothèse 2/b, le point P, qui a pour coordonnées (x/2; y/2; 0) dans le repère orthonormé de directions Ax, By et AB avec I pour origine, se promène dans le plan médiateur du segment AB en fonction des valeurs des deux variables x et y.
La contrainte pour MN énoncée à la question 3 se traduit par la condition xy = 2a².
Les coordonnées de P deviennent alors X = x/2 et Y = y/2 = (1/2)(2a²/x) = a²/x.
L'élimination de x conduit à Y = a²/2X , à compléter par Z = 0.
C'est l'équation d'une hyperbole équilatère.
Bj Priam
Dc le repère judicieux ici, c'est de prendre I comme origine du repère, de façon à ce que la cote reste nulle, c'est bien ça ?, de sorte que P se "promènera" ainsi tjs ds le plan médiateur de [AB], et aura une cote constante égale à 0 ?
En supposant que j'ai bien compris, à partir de tes éléments de réponse (pr lesquels je te remercie  ), voici ma rédaction de la Q3c :
), voici ma rédaction de la Q3c :
On a vu à la Q3a que lorsque (MN) est tangente à S, on a xy = 2 a².
Ds le r.o.n.
Pr :, ce qui revient à écrire xy = 2a², dc l'équation du lieu de P ds ce r.o.n. est
ce qui est l'équation d'une hyperbole équilatère.
_______________________________________________________________
Une rapide recherche internet sur G m'a amené sur un site qui écrit :
l'équation réduite de l'hyperbole équilatère est de la forme : x² - y² = a².
Ds un repère tourné d'un huitième de tour, (soit 45 °), son équation devient :
Est-ce en rapport avec l'inclinaison à 45 ° dt tu me parlais hier matin ?
je pense que oui...???
Merci de me dire si tu es d'accord avec ma rédaction ou ce qui ne va pas.
Oui, c'est bien, à part une chose : tu as fait une confusion entre x et y, coordonnées des points M et N, et x/2, y/2 qui sont les coordonnées du point P. C'est pour éviter cela que j'avais utilisé les lettres X, Y pour désigner les coordonnées de P.
Ainsi, la relation (x/2)(y/2) = a²/2 donne pour P Y = a²/2X.
A propos de l'inclinaison de 45° : oui, il y a un rapport. Tu pourrais t'en rendre compte en faisant une figure à plat du plan méditeur de AB, avec l'hyperbole et la trace du plan du lieu du point K. A noter que les points P et K sont confondus quand x = y = aV2.
tu as fait une confusion entre x et y, coordonnées des points M et N, et x/2, y/2 qui sont les coordonnées du point P. C'est pour éviter cela que j'avais utilisé les lettres X, Y pour désigner les coordonnées de P.
J'avais bien noté ces notations différentes, mais j'avoue que je ne comprenais pas trop mais que je pouvais m'en sortir par mon raisonnement, là d'après ce que tu m'écris, il semble que ça ait une importance, mais je ne comprends tjs pas ...
Ds le r.o.n. d' origine I, on est bienn d'accord que
Si non je comprends pas
 (pr l'instant)
(pr l'instant) 
Bonjour Priam
Donc le produit des coordonnées de P vaut a²/2.
je suis d'accord ; j'ai l'impression qu'on dit de fait la même chose mais avant de clore définitivement ce topic je veux être sur que je n'interprète pas mal.
N'hésite pas à me dire si j'écris des bêtises (sans vouloir abuser de ton tps)
ds le r.o.n.
Ds ces conditions:
on a la relation xy = 2 a²
les coordonnées de P sont
Et c'est là que je veux être sûr qu'on est bien d'accord et que finalement on dit la même chose :
Puisque
(1) s'écrit
Mais ne faut-il pas exprimer cette équation en "fonction", ou à partir des termes qui sont les coordonnées variables de M et de N, i.e. en remplaçant X par x/2 et Y par y/2, auquel cas on en revient à
NB : je ne cherche pas à avoir raison à tt prix ou à avoir le dernier mot, juste à bien comprendre et que ce ce soit bien clair pr moi.
merci pr ta patience.
Le mieux serait peut-être de définir le lieu de P par des équations paramétriques, avec x comme paramètre (par exemple) :
X = x/2
Y = y/2 = (2a²/x)/2 = a²/x.
Pr m'en tenir à l'énoncé, je veux juste savoir si l'équation demandée (celle du lieu de P, dc l'hyperbole) est tt aussi valable qd je reprends les parties variables des coordonnées de M et de N que lorsqu'on écrit l'équation avec les chgts de variables comme tu l'as fait avec X et Y, et que je comprends.
Maintenant je comprends aussi ou pense comprendre ce que tu suggères ; c'est une approche - je trouve - plus "mécanique" ou "cinématique" de la question, pr laquelle [MN] serait assimilé à un système matériel lié qui reste tangent à S, dt le milieu décrirait une courbe paramétrée (ou paramétrable) : si ce que j'écris n'est pas idiot, on dépasse qd même le cadre de l'énoncé. Je préfère m'en tenir à ce dernier qui m'aura permis d'approfondir ou de clarifier bon nombre de choses.
Dc je me permets de te demander, et ce sera p.e. la fin de ce topic, si ce que j'ai écrit ds mon message de 10 h 06 ce matin est juste ou erroné.
Merci de me dire.
Bonsoir pppa,
Dans ton repère d' origine , on a les coordonnées de
suivantes pour toutes les questions de ton énoncé:
Cela signifie que appartient au plan d' équation
, autrement dit le plan
En général, dans les différentes questions, on impose à et
des conditions qui se traduisent par une relation liant
et
, relation qui va lier
et
Le lieu de sera en général une courbe ou une portion du plan
Et on a:
ou encore
Dans cette question 3) et
sont liés par la relation
qui traduit le fait que
est tangente à la sphère.
On en déduit immédiatement que:
ou encore
Sans oublier que ,
et
donc que ,
et
On a donc affaire à une branche d' hyperbole du plan
Mais pour répondre à ta question:
Mais ne faut-il pas exprimer cette équation en "fonction", ou à partir des termes qui sont les coordonnées variables de M et de N, i.e. en remplaçant X par x/2 et Y par y/2, auquel cas on en revient à
Non:
Il faut au contraire éliminer les
C' est ce qu' on a fait.

Bonjour Cailloux
Merci pr ces éléments de réponse ; j'ai du mal à "accepter" la fin, mais j'y réfléchis.
Cailloux, excuse-moi, je ne veux en aucun cas t'obliger à quoi que ce soit mais si tu as du tps d'ici ce soir et que tu y as convenance, pourrais tu regarder mon sujet 380716 ; personne ne semble (pouvoir ou vouloir) s'y intéresser. Je suis persuadé que pr toi ce sera une formalité.
Merci bcp d'avance  .
.
Et tte aide sera la bienvenue .. 
Bonjour cailloux
Il faut au contraire éliminer les x et y
Je ne suis pas convaincu


 (ce qui ne signifie que je prétende avoir raison ou que tu aies tort), ou disons que j'ai (encore )du mal à comprendre ce dernier point)
(ce qui ne signifie que je prétende avoir raison ou que tu aies tort), ou disons que j'ai (encore )du mal à comprendre ce dernier point)
Est-ce que en fait
il faut au contraire éliminer les x et y
Oui finalement je commence à être un peu + convaincu...oui, on écrit l'équation du lieu de P, dc de la branche d'hyperbole, ds le PLAN rapporté au repère
ce qui me gêne/gênait, c'est qu'on peut tjs exprimer Xp en fonction de x et Yp en fonction de y, qui sont les données de départ, mais qui (ne) servent (que) à se repérer ds l'espace ds lequel se situe S. Mais à la Q3c, on change de repère et d'espace ( l'énoncé dit bien DEUX axes) et on écrit l'équation du lieu de P selon ce nouveau repère et l'espace qui lui est associé (en l'occurrence un plan, dc un espace de Dim 2) ; ah je suis de + en + convaincu..

C'est ça ; peux-tu me confirmer stp ?
Bonjour pppa,
C' est un peu ça; comme je te l' écrivais plus haut, dans cet exercice, et dans toutes les questions, les lieux de sont inclus dans le plan passant par
centre de la sphère et perpendiculaire à
Dans cette question 3)c), il se trouve que le lieu de est une courbe.
Dans le repère de ce plan, si
et
sont les coordonnées de
, cette courbe est nécessairement caractérisée par une relation liant
et
du genre
S' il subsiste des et
, on est bien embêté pour voir ce dont il s' agit.

cette courbe est nécessairement caractérisée par une relation liant Xp et Yp du genre F(Xp;Yp)=0
Ca je ne comprends pas ; la relation n'est elle pas

Mais c'est bien sûr.. 
Bon bah je crois que je peux considérer ce sujet comme globalement compris.
très instructif..
A bientôt, avec grand plaisir.
Merci à Priam et à Toi du tps que vs m'avez consacré 
Ah oui c'est vrai, on en avait parlé ; bon ça ns fait 2 sujets en instance (la descro de BigJo et le prolongement de ce sujet).
NB : ce pb est extrait de l'épreuve du bac qu'on faisait passer en fin de 1ère en 1962, qd il se passait encore en 2 parties pr les principales matières. (pr les 2 exercices, je me suis débrouillé tt seul).
Je vs parle d'un temps
que les moins de 55 ans
ne peuvent pas connaître
le bac en se temps là....