Bonsoir,

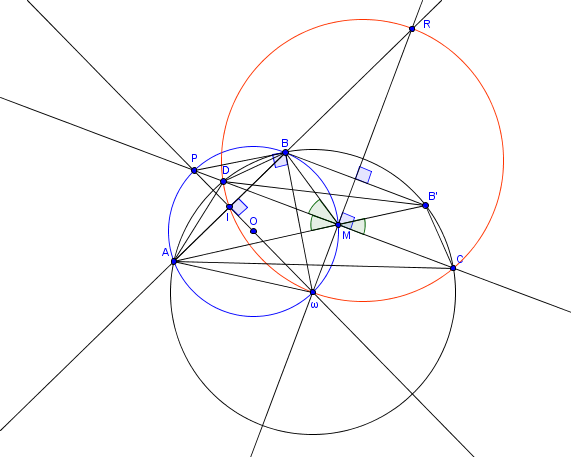
D' abord une figure:



On a

Les points et sont donc cocycliques et ton quadrilatère est inscriptible dans un cercle (ce n' est pas un trapèze...)

C' est un début...

Bonjour

Lorsque tu mets MA.MB , c'est un produit scalaire ?

Pour prouver que CD // BB' , intéresse toi à la nature du triangle BMB', ensuite la bissectrice issue de M dans ce triangle, et à la "position relative" de cette bissectrice par rapport à la bissectrice intérieure de AMB

Re

Montrer que les triangles DMB et CMB' sont isométriques

Bonsoir Cailloux, Bonsoir Zorrito

merci d'avoir commencé à intervenir rapidement.

Le schéma de  cailloux va bien m'aider ; c'est clair
1/ le quadrangle ACB'D n'est pas un trapèze, mais l'ordre du schéma de Cailloux est le même que le mien et pas celui de l'énoncé
2/ avec géogébra c'est mieux !

je vais commencer à réfléchir (demain) à partir de ce que vs m'avez écrit

>> Zorrito : d'après le chapitre duquel;provient le pb, oui il s'agirait de produit scalaire, il faudrait donc lire , en tt cas je le considère comme tel et ça me paraît cohérent, j'ai recopié l'énoncé tel que.

>>Cailloux : excellent WE ; alors ça t'inspire ?? Un peu ... bcp  .... passionnément
moi c'est limite à la folie (mdr)

Bonjour à tous, et en particulei aux participants à ce pb

J'ai analysé les premiers éléments que vs m'avez fournis.
Voici ce que je pense avoir compris :
B' est ds le prolongement de [MA] et M est le milieu de [CD]
Donc (AB') et (CD) sont sécantes en M (1) avec , d'après l'énonce :
MB' = MB
MC² = MD² donc MC = MD
et MC² = MC MC = MC MD = MA MB = MA MB' (2)

De (1) et (2) je conclus que la puissance de M par rapport à un cercle passant par A et B' est la même que celle d'un cercle passant par C et D,
par conséquent (??, est ce que le raidonnement est correct?), A, B', C et D sont cocycliques et le quadrangle joignant ces 4 points en inscrit ds un même cercle.

Mais j'ai 2 questions :
1/ici on ne considère que des mesures ou des distances en valeurs 'naturelles', sans considération de mesure algébrique, or il me semblait que la puissance d'un point M par rapport à un cercle tel que une droite passant par M coupe le cercle en P et Q par ex est égale à ?
2/Cailloux, comment as-tu déterminé C et D sur le schéma pr que les 5 points A B B' C D tombent harmonieusement sur le même cercle ? Pr mon schéma j'avais fait des calculs avec des mesures de MA, MB et des racines carrées pr trouver C et D ; j'ai aps l'impression que ça ait été aussi compliqué pr toi ? Est-ce qu'il y a une propriété  que j'ai oubliée qui tient au fait que c et D sont sur la bissectrice intérieure de
Ds l'attente de vos réponses ou commentaires je vais considérer que ce que j'ai fait est bon ou compris pr essayer d'avancer

Merci bcp pr votre aide (et vos aides futures, je vais en avoir besoin, mais je suis sûr que grâce à vous je vais finir par tt comprendre , enfin j'espère!!!

Bonjour
je faisais des recherches sur les conditions de cocyclicité des 4 points A b C D et comment déterminer .
J'ai pas (encore trouvé) mais par contre je ne suis plus surpris par le fait qu'on demande ce qu'est le quadrangle A B' C D ds cet ordre ; il s'agiit d'un quadrilatère CROISE inscriptible ds pr les raisons qu'on a vues.

Ca m'avance pas bcp mais c'est déjà + clair !

bonsoir

j'ai trouvé sur internet
http://www.maths.ac-aix-marseille.fr/debart/geoplan/triangle_pt_caract.html
la condition nécesaire et suffisante pr qu'un quadrangle soit inscriptible




"ABCD est inscriptible si et seulement si IA × IB = IC × ID.
IA × IB est la puissance du point I par rapport au cercle circonscrit au quadrangle".

Ce qui correspond à ce qu'on a établi pr A, B',C,D
avec M
Reste à trouver  l'équivalent de M pr A,B,C et D
à moins qu'on puisse en faire la preuve autrement

et je ne fais pas le lien entre   milieu de l'arc AMB et centre du cercle ds lequel ABCD est inscrit

Merci de m'aider à avancer

Bonjour,

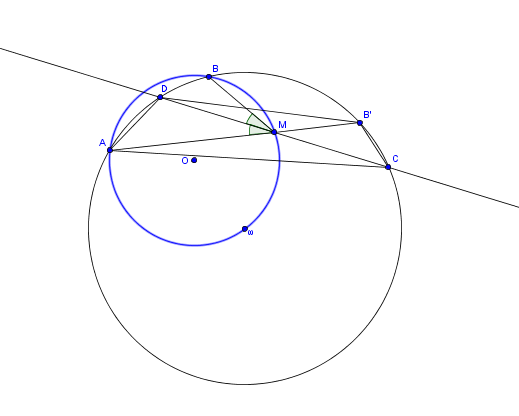
Un nouveau dessin:



La perpendiculaire en à est la médiatrice de mais aussi la bissectrice extérieure de

Les triangles et sont non seulement isométriques (à prouver) mais aussi symétriques par rapport à cette médiatrice.
Si bien que et sont symétriques par rapport à cette médiatrice.

recoupe en et on a:



On en déduit que est le milieu de l' arc de qui ne contient pas

Autrement dit appartient à la médiatrice de

La médiatrice de (qui est aussi celle de ) recoupe en diamétralement opposé à (puisque est droit)

Donc , milieu de l' arc , est le centre du cercle défini par les points et qui passe aussi par et

Une petite réciproque permet d' écrire que le lieu de et est ce cercle de centre passant par et

Bonsoir Cailloux ( et aux autres lecteurs ed ce sujet)

merci pour le schéma et les explications qui me font avancer dans la résolution du pb.

Voici comment je démontre que les triangles (trg ds la suite) MBD et MB'C sont isométriques et la cocyclicité de A, B , C et D.

On a MC² = MD², donc MC = MD (1) (en distance) et MB = MB' (2)
(CD) est la bissectrice intérieure de , donc = ; de +, et sont opposés par le sommet M, donc ils sont égaux et = (3).

De (1),(2) et (3) on déduit que les trgs MBD et MB'C sont isométriques, soit l'un est l'image de l'autre par une isométrie, en l'occurrence une symétrie axiale. M étant le point commun à ces 2 trgs, on en déduit que M appartient à l'axe de symétrie cherché.

Sachant que MC = MD et que (CD) est la bissectrice intérieure de issue de M, l'axe de symétrie cherché est la perpendiculaire à (CD) passant par M, soit la bissectrice extérieure en M de . Enfin B' étant l'mage de B par cette isométrie, [BB'] est coupé orthogonalement en son milieu  par la bissectrice ext de , qui est dc la médiatrice de [BB'], ce que confirme l'égalité MB = MB'.

Conclusion :
on sait que :
- MC = MD
- MB' = MB
- C et D d'une part, B' et B d'autre part sont symétriques par rapport à un même axe de symétrie

donc B appartient au même cercle que que B', C et D dont on sait qu'ils sont cocycliques avec A, par conséquent A, B , C , D sont sur un même cercle.

J'essaie amintenant de prouver que ce cercle a pr centre .

Il y a 2 points que je ne comprends pas ds ta démonstration ; peux tu me réexpliquer stp :

1/  P médiatrice  de [AB]

2/ à la médiatrice de [CD] et de [BB'], donc
   B = B' et C = D.
   Mais comment en déduit-on que est le centre du cercle passant par ces points ? Car je me dis on a aussi MB = MB' et MC = MD pour autant M n'est pas le centre du cercle qui passe par ces points.

Peux-tu m'expliquer stp ?

Merci d'avance

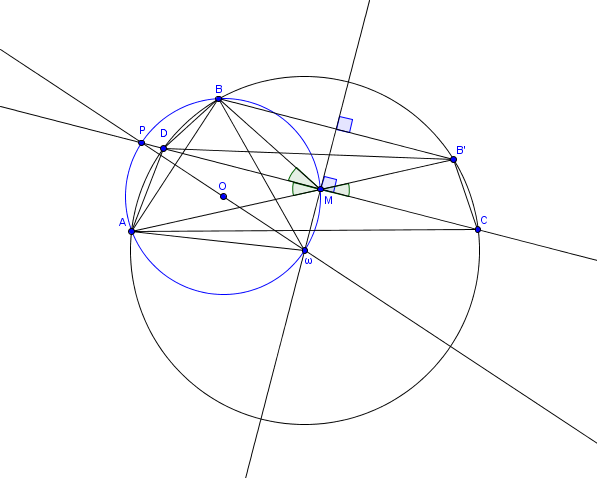
Re bonsoir pppa,

Un dessin allégé:


1)Avec , est le milieu de l' arc (situé du côté de la corde qui ne contient pas )

est donc axe axe de symétrie pour cette corde donc la médiatrice de

2) On sait que et sont cocycliques.

Appelons provisoirement le centre du cercle en question .

appartient à la médiatrice de donc à la médiatrice de ainsi qu' à la médiatrice de puisque

intersection de la médiatrice de et de celle de est donc en

et on a:



Bref les 5 points appartiennent à un cercle de centre

Non ?

Un dessin pour la 2) que je trouve plus facile...

Bonjour Cailloux,

Ca y et j'ai compris comment on explique que est le centre du cercle  qui passe par A, B , C et D. Pr ça il me fallait comprendre prquoi P est un diamètre ( le trg PM est rectangle en M, donc son hypothénuse P est un diamètre de , et connaître le théorème (que j'ai retrouvé ds un livre de cours) qui dit que tout diamètre perpendiculaire à une corde  [AB] passe par le milieu de cette corde  et par le milieu des arcs qu'elle sous-tend (P et ) ; en fait c'est en lisant le théorème "aà l'envers" que j'ai compris ; du coup je prouve aussi que milieu de de l'arc AB du côté de M.

Avant de passer à la question 2 on demande de déduire de tt ce qui précède les lieux de C et D lorsque M décrit en entier, et là il me reste une question : comment as tu fait pr positionner c et D t.q. MC² = MD² = MA.MB ; moi sur mon schéma j'ai dû faire des calculs bien compliqués et apparemment pas toi. peux- tu m'expliquer comment tu as fait  et est-ce que ça peut m'aider pr répondre à la question ; merci d'avance

Bonsoir Cailloux

je relisais ce que tu écris pr essayer de conclure la 1ère question.
En fait : A et B sont fixes, tandis que C et D dépendent de la position de M, variable, du fait de la relation MC² = MD² = MA.MB.

Quelle que soit la position de M sur ( ou qd M décit en entier pr reprendre les termes de l'exercice), A, B C et D seront cocycliques sur le cercle de centre , avec A et B fixes.
J'en conclus que les lieux de C et D qd M décrit seront toujours l'intersection de la bissectrice intérieure de avec le cercle de centre .
Je me pose qd même la question : qu'est ce qui se passe qd M = A ou M = B ? Je crois que le triangle AMB est dit aplatin mais comment positionner sa bissectrice intérieure passant par M ? et MA.MB sdoit être égal à 0 ? Donc MC² = MD² = 0 ; alors les points C et D seraient confondus avec M, lui même confondu avec A ou B ?
Est-ce que ça te paraît  juste ?

Bonsoir pppa,

Citation :
on demande de déduire de tt ce qui précède les lieux de C et D lorsque M décrit en entier

Ah! je n' avais pas vu 21h36

Si la sécante issue de est tangente par exemple en au cercle :

Les points et sont confondus et on a bien

La droite devient à la limite

La droite devient à la limite la tangente au cercle en

La droite devient à la limite .

et la propriété "bissectrice" est encore vraie...

Re bonsoir Cailloux (et d'autres amateurs éventuellement) !

Je commence à réfléchir à la question 2 grâce à ton dessin.
La difficulté c'est de montrer = parce que une fois ça établi on constate que ces 2 produits sont la puissance de P par rapport à un même cercle passant par I, , C et D.
En 1 on a déjà montré que (P) (AB) et  leur intersection est I ; donc IR est un triangle rectangle en I, d'hypoténuse [R], qui correspond au diamètre d'un cercle passant par ces 3 points ; or on a établi + haut (sauf que je l'ai pas encore prouvé) que I et sont cocycliques ; donc R à ce même cercle ; est-ce que ce sont les bonnes pistes ?

Merci pr ton aide

Voilà comment je vois la chose pour la 2):



en utilisant les propriétés du produit scalaire avec les projections de vecteurs.

Or est la puissance de par rapport au cercle (le cercle noir)

et donc et la conclusion...

excuse-moi mais je ne comprends pas PB² puissance de P par rapport au cercle noir ; j'aurais dit par rapport au cercle rouge puisqu'on (TU) a prouvé que PB² = . Tu as sûrement raison, il faut juste que je comprenne prquoi:merci

Imagine un cercle et un point extérieur à ce cercle.

Une sécante variable issue de coupe ce cercle en et .

Les 2 positions limites de ces sécantes sont les 2 tangentes issues de à ce cercle.

Les points et sont alors confondus au point de contact de la tangente.

et on a la puissance de par rapport à qui vaut:

où et sont les deux points de contact (dans notre exercice, il s' agit de et )

et sont bien les tangentes issues de au cercle noir.

Oui, les tangentes ...
Et surtout PA = PB puisque P est sur la bissectrice de [AB], d'ou PB² = , enfin si j'ai bien compris ?

Sinon pr le reste pourras-tu me dire si ma démonstration de la 2/ ds mon message de 22 h 02 est acceptable . merci

On avance, on avance.....

Dans l' ensemble, c' est ça...

Avec , on sait que les points et sont cocycliques.

D' autre part comme et que appartient à qui passe par le centre du cercle rouge (c' est ce que tu as oublié d' écrire je crois ?), alors est un diamètre de ce cercle.

C'est à dire que je ne sais pas prouver que (M) passe par le centre du cercle rouge.....
La démonstration avec le triangle rectangle me plaisait bien, mais apparemment c'est pas suffisant ? Comme l'énoncé parle de (M) qui coupe (AB) en R, a priori je ne vois pas comment connaître le centre du cercle rouge.
Si tu peux m'en dire + , ce soir ou demain, moi je vais pas tarder à décrocher, pr ce soir, car je suis sûr qu'avec ton aide et un peu de ma réflexion, je vais aller au bout de ce pb.

Merci encore pr tt ce que tu fais ...

Bonsoir Cailloux,

je suis bien sûr d'accord avec tes réponses ; pr la première notamment c'est la honte puisqu'il suffit de réappliquer le théorème :
tout diamètre perpendiculaire à une corde  [CD] passe par le milieu de cette corde (M)  et par le milieu des arcs qu'elle sous-tend ( et R qui est diamètralement opposé) et de le lire à l'envers, alors que je l'avais cité ds mon message de 18 h 44

pr la question 3 j'aurai spontanément tendance à chercher à montrer que = ou = mais je ne vois pas de droites ou demi-droites qui permettraient de l'établir.
Pr la relation ² = ² = j'ai trouvé - mais sans voir le rapport avec l'exercice - que c'est la relation de Newton qui se vérifie si C et D sonr "conjugué harmoniques" avec A et B, c'est -à-dire si on a =  - .

Ceci pr dire que j'ai cherché avant de (te) demandre encore une fois de l'aide pr terminer cet exercice.

D'avance merci de me dire si tu peux me donner une piste pr terminer cet exercice qui nécessite un grand savoir en géométrie je trouve.



Enfin, peux-tu me dire stp
1/ comment on fait une citation (je n'ai pas trouvé ds le mode d'emploi du forum)
2/ les dessins,  tu les as faits avec géogébra ?

Bonsoir pppa,

On va commencer par cette histoire de bissectrice:

C et D étant symétriques par rapport à (\omega R)

Euh, mince, l' icône LaTeX a disparu!!

Je vais attendre un petit peu...

Bon, elle est est revenue

et étant symétriques par rapport à , on a:



Tu ne vois pas une histoire d' angle inscrits dans le cercle rouge ?

Bonjour Cailloux

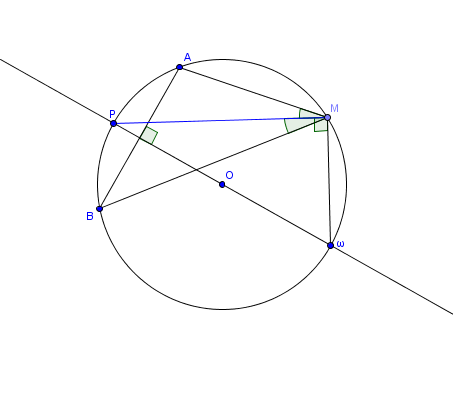
Un dernier dessin pour la dernière partie de 3)



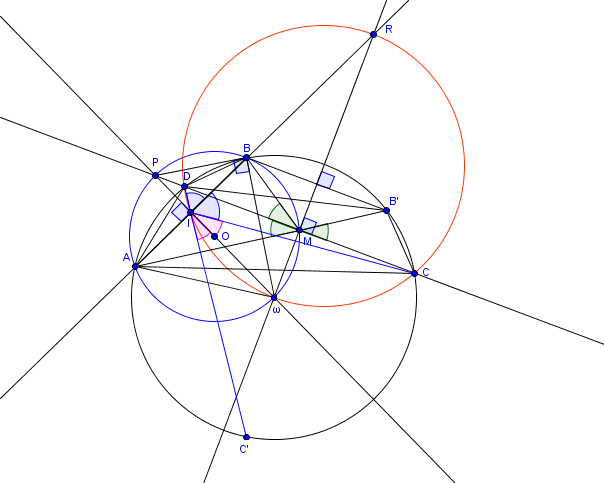
On se retrouve dans les mêmes conditions que la 1) (un genre de réciproque).

J' ai construit symétrique de par rapport à qui appartient donc au cercle noir et tel que

On peut démontrer que les points sont alignés.

Puis parler puissance de par rapport au cercle noir...

Bonjour Cailloux

merci bcp pr cet ultime schéma qui devrait me permettre de finaliser le pb. On (je) ne va pas s'arrêter si près du but..

Bien sûr du théorème de l'angle inscrit  je déduis que =   ;il fallait juste considérer l'arc CR et pas se focaliser sur l'arc CD comme je l'ai fait.

Avec ton schéma, je comprends que si on établi que D, I et C' sont alignés on aura :
puissance de I par arpport au cercle noir = = or = ² = ²  et IC = IC' puisque C' est le symétrique de C par rapport à la bissectrice intérieure de .

Reste à établir l'alignement de  D, I et C' ; là je dois m'absenter mais laisse moi chercher, je reviens sur le site si j'ai trouvé ou si vraiment j'y arrive pas ; on va essayer de terminer aujourd'hui.

A + tard ; merci bcp

Bon me revoilà ; voilà ce que je propose pr terminer la question 3.

On a établi = = .

C'   est l'image de C par une symétrie axiale d'axe (I) (et on m'a appris que sauf précisoin contraire, une symétrie axiale est une symétrie orthogonale, ce qui est le cas ici ; donc les distances de C et de C' à (I) sont égales). On en déduit que (I) est la bissectrice intérieure de et donc que = = .

On a aussi démontré que (AB) confondue avec (IR) est la bissectrice intérieure de et que (P) coupe [AB] ( (IR))  à angle droit en I

Bonsoir ppda,

Je crois bien que tout y est (un peu dans le désordre), mais tu as bien compris le principe.

Juste une remarque:

Si l' on s' occupe des puissances donc des mesures algébriques, on a:



car étant intérieur au cercle noir, sa puissance par rapport à ce cercle est négative.

On passe ensuite aux distances (positives):



que l' on peut écrire:



Bref, ton exercice est terminé...

Bonjour Cailloux,

je suis vraiment content d'avoir pu résoudre ce pb grâce à toi ; seul je n'y serais pas arrivé ; je crois que j'ai appris bcp ou réappris bcp en le faisant avec ton aide et les nombreux schémas




tu m'avais dit ( cf les exercices de trigo) que tu serais ma roue de secous pr ce pb ; je dirais plutôt que tu as été mes 4 roues motrices, et moi la roue qui tournait ds le vide

Encore un grand merci pr tt le temps que tu (m')as donné


c'est vrai que tt est un peu ds le désordre mais au moins j'ai tt compris ce que tu m'as expliqué ; ds les jours qui vienne j'essaierai de faire une sunthèse ordonnée de tt ça et je la posterai ; il y aura dc peut être une suite et fin à ce sujet.

Sinon à bientôt peut être sur d'autres sujets ; pr ma part ce sera avec très grand plaisir

Ehhhhhhh, mon pseudo  c'est pas ppDa comme tu as écrit , c'est pppa.

Ppda est qqn pr qui j'ai bcp de respect (surtt depuis qu'il s'exprime hors de la chaîne de laquelle il a été "remercié") pr usurper +/- son identité

Ohhh! Désolé d' avoir écorché ton pseudo!

Bon, en prime pour finir et pour me faire pardonner, un petit exercice qui se rapproche du sujet:

2 cercles sont sécants en 2 points distincts et .

Soit et les points de contact d' une de leur tangente commune.

Montrer que les aires des triangles et sont égales.

En tout cas, ton exercice m' a bien plu et si on se recroise sur l' ce sera aussi avec plaisir...

Bonjour Cailloux

Pr être sûr que ja pars sur une bonne piste, a priori ça se résoudrait avec les puissances d'un point par rapport à un cercle ?

Merci de me dire

Bonjour pppa (sans fôtes)

Re bonjour Cailloux

Alors voilà pr l'instant ce que ça m'inspire :

Les deux triangles ont un côté commun [MN]. l'aire d'un triangle se calcule par la formule . En choisissant [MN] comme base des 2 triangles et en appelant R et S les projections orthogonales de P et de Q sur [MN], il faudrait prouver que PR = QS

J'ai fait un schéma (désolé je ne maîtrise pas encore géogébra )mais je pense que tu me suis

Après pr le rapport avec la puissance d'un point par rapport à un cercle, voilà ce que je comprends :
Soit A un point quelconque de (MN) ; sa puissance par rapport aux 2 cercles est la même : .
Ce que je ne vois pas, c'est le lien avec la tangente (PQ) commune aux 2 cercles.

Suis-je sur une piste intéressante ? Si oui peux tu m'aider à trouver en quoi la tangente peut aider à résoudre l'exercice.

Merci d'avance. C'est très intéressant, parce qu'a priori on ne devine pas que les 2 triangles ont même aire !

Bonsoir Cailloux

j'ai un peu avancé par rapport à ce que tu as dit, en plaçant A = (PQ) (MN)
ds ces conditions la puissance de A par rapport au cercle passant par P vaut ² = et  par rapport au cercle passant par Q vaut ² = ; donc AP² = AQ²  soit AP = AQ (ce que je vérifie sur mon schéma)

Après je réfléchissais mais je ne sais pas (et surtt j'aboutis pas) si je dois considérer les triangles PNA et QNA (tu l'auras compris (PQ) est la tangente qui passe du côté de N) et leurs hauteurs qui sont resp PR et QS, dt je cherche à prouver l'égalité ; en tt cas ces 2 triangles ne sont pas isométriques et donc on ne peut pas en déduire tt de suite que leurs hauteurs sont = puisque l'angle des 2 côtés égaux n'a VISIBLEMENT pas la même mesure.

Voilà où j'en suis ; il doit me manquer un théorème ou une formule pr calculer ou vérifier lahauteur d'un triangle qui n'est pas rectangle  Ou alors ily a les triangles rectangles ARP et AQS mais là je n'aboutis pas ; est ce que je m'approche qd même de la solution ?

Merci

bonne soirée  

Ah et bah t'as déjà répondu !!

J'étais ds le jardin avec mon PC portable et je viens de remonter la haut ; je me suis reconnecté par hasard sur l'île...

Dernière question sur le sujet ; tu as sûrement raison et je ne dois avoir en tête ts les cas d'égalité des triangles ; est-ce qu'il n'est pas nécessaire que les angles de même mesure portent sur 2 côtés égaux pr dire que les triangles sont isométriques ? C'est pr ça que j'avais pas conclu parce que je ne savais pas prouver que AR = AS.
Alors est-ce que le fait que les triangles soient rectangles permet de conclure à l'égalité comme tu l'as fait ??

C'est idiot comme question ou je chicane ??

Non ce n' est pas idiot, mais tu as oublié la géométrie de seconde...

Il y a 3 cas d' égalité de triangles:

1) 3 côtés égaux.

2) un angle égal compris entre deux côtés égaux.

3) un côté égal adjacent à 2 angles égaux.

Ici, on a démontré que les triangles et avaient leurs 3 angles égaux.

et les côtés et égaux.

On est dans le cas 3)...

Eh OUI ; ce sont des triangles rectangles, dt on sait que un de leurs angles non droit sont opposés par le sommet ; donc on peut en déduire que leurs 3 angles sont égaux et un de leurs côtés étant égaux; les triangles sont égaux.
Super ; très intéressant.

D'ici qqs jours j'essaierai de faire une synthèse sur le premier pb parce que tt est très découpé. Donc ne sois pas surpris s'il y a un complément à ce topic.

Sinon à bientôt avec grand plaisir sur d'autres sujets


MERCI

De rien pppa bonne nuit

Correction complète du problème ( je suis juste pas sûr que 1c soit démontré rigoureusement):

1a/ Nature du quadrangle AB'CD
M, A et B' sont alignés. M, C et d sont alignés.
On a : -  (² = ²) (MC² = MD²) (MC = MD)
- MC² = MD² = MA.MB
- MB' = MB
Et on sait que M est aligné avec C et D d'une part, avec A et B' d'autre part.
Donc , donc ces produits sont égaux à la puissance de M par rapport à un même cercle passant par A, B', C et D. Par conséquent,  le quadrangle AB'CD est inscriptible.

1b1/ Cocyclicité de A,B,C et D
Etude des triangles MDB et MCB'.
On a : -  MC = MD et MB = MB'
- , puisque (MD) est la bissectrice intérieure de ,
- , angles opposés par le sommet,
Donc

Tm : Si deux triangles ont un angle de même mesure ( pour l'un, pour l'autre) compris entre 2 côtés resp. de même longueur (MD et MB pour l'un, MC et MB' pour l'autre), alors ces 2 triangles sont isométriques.
Par conséquent,  ces 2 triangles MDB et MCB' sont image de l'autre par une isométrie, en l'occurrence une symétrie axiale ; soit la bissectrice extérieure de l'axe de symétrie correspondant, et s la symétrie axiale caractérisant cette isométrie. On a :
s(M) = M ; s(D) = C puisque MC = MD ; s(B) = B', donc B et B' sont symétriques par rapport à la bissectrice extérieure de  \widehat{AMB}, qui est aussi la médiatrice de [CD], donc la médiatrice de [BB'].
On sait que A, B', C et D sont cocycliques (§1a) ; soit G le centre de ce cercle, on a : GA = GB' = GC = GD, donc G est sur la médiatrice de [CD], donc sur la médiatrice de [BB'] ; Par conséquent,  GB = GB' et B appartient au cercle passant par A, B', C et D.

1b2/  Centre du cercle passant par A, B, C et D
(CD), bissectrice intérieure de , recoupe en P, donc , avec P, A et B sur , donc P est le milieu de l'arc AB qui ne contient pas M.
M est le milieu de [CD], donc la bissectrice extérieure de est la médiatrice de [CD]. On suppose que cette médiatrice n'est pas tangente à , donc qu'elle le recoupe en K. (CD) (MK) = M ; P, M et K sont sur et PMK est un triangle rectangle en M, donc [PK] est un diamètre de , et K est diamétralement opposé à P sur . Par conséquent,  P étant le milieu de l'arc AB ne contenant pas M, le point K qui lui est diamétralement opposé est le milieu de l'arc AB contenant M.
Soit O le centre de et I  le milieu de la corde [AB]. P étant le milieu de l'arc AB, le diamètre [KP] coupe la corde [AB] orthogonalement en son milieu I, et KA = KB.
Mais K appartient aussi à la médiatrice de [CD], donc à celle de [BB'] ; on a donc KC = KD = KB' = KB = KA..
Conclusion :
- K est le milieu de l'arc AB contenant M
- K est le centre d'un cercle passant par A, B, C, D et B'

Donc K est le point cherché.

1c/ Lieu de C et D lorsque M décrit
lorsque M décrit , C et D appartiennent au cercle passant par A, B et B'. Toute sécante issue de P (intersection de [CD] avec   et  milieu de l'arc AB) au cercle de centre coupe ce cercle en C et D (evtl confondus avec A ou B), t.q. (CD) soit la bissectrice intérieure de / et MC² = MD² = MA.MB. Le lieu cherché est donc le cercle de centre tout entier.

2a/ Vérification de l'égalité P, I et sont alignés, dc = PB².
(PB) est la tangente en B au cercle de centre ; dc PB² est la puissance de P par rapport à ce cercle. Mais P (CD) et C et D appartiennent au cercle de  centre ; dc est aussi la puissance de P par rapport à ce cercle ; p.c. :  

2b/ Cocyclicité de I, C et D
De 2a/, on sait que I, , C et D sont cocycliques.
On a de plus :
- R (M) (donnée du pb)
- à la médiatrice de [CD] (Cf conclusion de 1b)
- M est le milieu de la cordre [CD] du cercle ,
donc R à ma médiatrice de [CD] et (R)(CD)

Tm : la perpendiculaire au milieu d'une corde d'un cercle passe par le centre de ce cercle et par le milieu des arcs sous-tendus par la corde

Conclusion : [R] est le diamètre du cercle passant par I, , C et D, et est le milieu de

3a/ (AB) est la bissectrice intérieure de

On a établi (Cf 2b) que (R) est la médiatrice de [CD], donc C et d sont symétriques par rapport à (R) et =
D'après le tm de l'angle inscrit, selon lequel 2 angles inscrits ds un même arc de cercle sont égaux, on a  : = , = et = ; or = , dc = , dc (IR) est la bissectrice intérieure de , et (IR) est confondue avec (AB)  puisque I [AB] et R (AB) (donnée de l'exercice en 2)

3b/ Montrer que ² = ² = IC.ID

On sait que :
-I est le milieu de [AB],
- A,B,C, et D sont cocycliques sur le cercle de centre ,
- (P) est la médiatrice de [AB] (cf 1b2), donc I (P),
- I = (AB) (P), dc IB est un trg rtg en I (*).

On construit C', point du cercle passant par A, B, C et D de centre , t.q. Correction complète du problème :

1a/ Nature du quadrangle AB'CD
M, A et B' sont alignés. M, C et d sont alignés.
On a : -  (² = ²) (MC² = MD²) (MC = MD)
- MC² = MD² = MA.MB
- MB' = MB
Et on sait que M est aligné avec C et D d'une part, avec A et B' d'autre part.
Donc , donc ces produits sont égaux à la puissance de M par rapport à un même cercle passant par A, B', C et D. Par conséquent,  le quadrangle AB'CD est inscriptible.

1b1/ Cocyclicité de A,B,C et D
Etude des triangles MDB et MCB'.
On a : -  MC = MD et MB = MB'
- , puisque (MD) est la bissectrice intérieure de ,
- , angles opposés par le sommet,
Donc

Tm : Si deux triangles ont un angle de même mesure ( pour l'un, pour l'autre) compris entre 2 côtés resp. de même longueur (MD et MB pour l'un, MC et MB' pour l'autre), alors ces 2 triangles sont isométriques.

Par conséquent,  ces 2 triangles MDB et MCB' sont image de l'autre par une isométrie, en l'occurrence une symétrie axiale ; soit la bissectrice extérieure de l'axe de symétrie correspondant, et s la symétrie axiale caractérisant cette isométrie. On a :
s(M) = M ; s(D) = C puisque MC = MD ; s(B) = B', donc B et B' sont symétriques par rapport à la bissectrice extérieure de  \widehat{AMB}, qui est aussi la médiatrice de [CD], donc la médiatrice de [BB'].
On sait que A, B', C et D sont cocycliques (§1a) ; soit G le centre de ce cercle, on a : GA = GB' = GC = GD, donc G est sur la médiatrice de [CD], donc sur la médiatrice de [BB'] ; Par conséquent,  GB = GB' et B appartient au cercle passant par A, B', C et D.

1b2/  Centre du cercle passant par A, B, C et D
(CD), bissectrice intérieure de , recoupe en P, donc , avec P, A et B sur , donc P est le milieu de l'arc AB qui ne contient pas M.
M est le milieu de [CD], donc la bissectrice extérieure de est la médiatrice de [CD]. On suppose que cette médiatrice n'est pas tangente à , donc qu'elle le recoupe en K. (CD) (MK) = M ; P, M et K sont sur et PMK est un triangle rectangle en M, donc [PK] est un diamètre de , et K est diamétralement opposé à P sur . Par conséquent,  P étant le milieu de l'arc AB ne contenant pas M, le point K qui lui est diamétralement opposé est le milieu de l'arc AB contenant M.
Soit O le centre de et I  le milieu de la corde [AB]. P étant le milieu de l'arc AB, le diamètre [KP] coupe la corde [AB] orthogonalement en son milieu I, et KA = KB.
Mais K appartient aussi à la médiatrice de [CD], donc à celle de [BB'] ; on a donc KC = KD = KB' = KB = KA..
Conclusion :
- K est le milieu de l'arc AB contenant M
- K est le centre d'un cercle passant par A, B, C, D et B'

Donc K est le point cherché.

1c/ Lieu de C et D lorsque M décrit
lorsque M décrit , C et D appartiennent au cercle passant par A, B et B'. Toute sécante issue de P (intersection de [CD] avec   et  milieu de l'arc AB) au cercle de centre coupe ce cercle en C et D (evtl confondus avec A ou B), t.q. (CD) soit la bissectrice intérieure de / et MC² = MD² = MA.MB. Le lieu cherché est donc le cercle de centre tout entier.

2a/ Vérification de l'égalité P, I et sont alignés, dc = PB².
(PB) est la tangente en B au cercle de centre ; dc PB² est la puissance de P par rapport à ce cercle. Mais P (CD) et C et D appartiennent au cercle de  centre ; dc est aussi la puissance de P par rapport à ce cercle ; p.c. :  

2b/ Cocyclicité de I, C et D
De 2a/, on sait que I, , C et D sont cocycliques.
On a de plus :
- R (M) (donnée du pb)
- à la médiatrice de [CD] (Cf conclusion de 1b)
- M est le milieu de la cordre [CD] du cercle ,
donc R à ma médiatrice de [CD] et (R)(CD)

Tm : la perpendiculaire au milieu d'une corde d'un cercle passe par le centre de ce cercle et par le milieu des arcs sous-tendus par la corde

Conclusion : [R] est le diamètre du cercle passant par I, , C et D, et est le milieu de

3a/ (AB) est la bissectrice intérieure de

On a établi (Cf 2b) que (R) est la médiatrice de [CD], donc C et d sont symétriques par rapport à (R) et =
D'après le tm de l'angle inscrit, selon lequel 2 angles inscrits ds un même arc de cercle sont égaux, on a  : = , = et = ; or = , dc = , dc (IR) est la bissectrice intérieure de , et (IR) est confondue avec (AB)  puisque I [AB] et R (AB) (donnée de l'exercice en 2)

3b/ Montrer que ² = ² = IC.ID

On sait que :
-I est le milieu de [AB],
- A,B,C, et D sont cocycliques sur le cercle de centre ,
- (P) est la médiatrice de [AB] (cf 1b2), donc I (P),
- I = (AB) (P), dc IB est un trg rtg en I (*)

On construit C', point du cercle passant par A, B, C et D, de centre , t.q. = , dc IC' = IC.

On a :
- = + = rd (Cf (*)) (**)
- = et = = (***),

de (**) et (***) il vient   + = rd et = + + = ( + ) + = rd, p.c. C', I et D sont alignés.

Conclusion : = ² =  ² est la puissance de I par rapport au cercle de centre ,
est aussi la puissance de I par rapport au cercle de centre , ces produits sont égaux en valeur algébrique et en valeur absolue, or IC' = IC, dc IC'.ID = IC.ID = ² =  ²

MILLE EXCUSES , un problème de copier coller ds le message précédent.
Ds le 3b le message s'est recopié ; le 3 b est terminé à la fin du message

Désolé