Inscription / Connexion Nouveau Sujet
Graphique des dérivées
Bonjour voici le premier exercice de maths de mon frère il y a un graphique et là il y a des exponentiels d'après ce qu'il m'a dit donc comme moi j'en ai jamais entendu parler je viens vers vos lumières.
Merci de votre aide, voici le sujet:
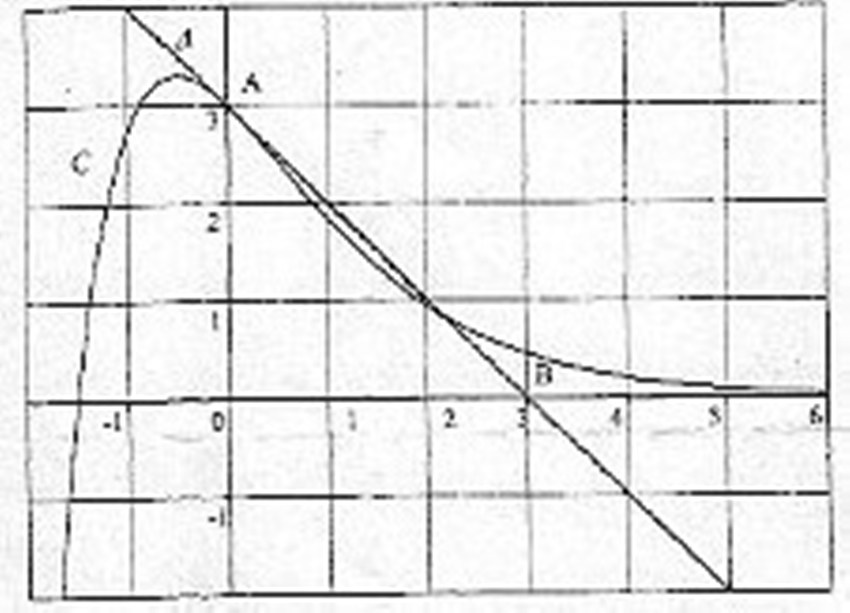
La courbe C ci-dessous représente dans un repère orthonormal (O; i ,j) une fonction f
définie sur  par f(x) = (ax + b) exposant-x, ou a et b sont deux nombre réels.
par f(x) = (ax + b) exposant-x, ou a et b sont deux nombre réels.
la droite  est la tangente à la courbe C au point A d'abscisse 0. Cette tangente passe par le point B de coordonnées (3;0).
est la tangente à la courbe C au point A d'abscisse 0. Cette tangente passe par le point B de coordonnées (3;0).
a) Déterminer graphiquement f(0).
b) Déterminer graphiquement ou par le calcul, f'(0).
c) Déterminer les valeurs des nombres réels a et b.
Merci de votre aide
bonsoir
f(x)=(ax+b)e-x
le point A(0;3)appartient au graphe de la fonction f donc f(0)=3 ce qui entraine que b=3; en effet f(0)=(a*0+b)e0=b (rappel e0=1)
équation de la droite  :
:
soit y= x+
x+ l'équation de
l'équation de  comme elle passe par les 2 points A(0;3) et B(3;0)on peut écrire que 3=
comme elle passe par les 2 points A(0;3) et B(3;0)on peut écrire que 3= 0+
0+ et 0=
et 0= *3+
*3+ soit 3=
soit 3= et 0=3
et 0=3 +3donc
+3donc  =-1
=-1
d'où équation de  :y=-x+3
:y=-x+3
or le coefficient directeur de la tangente au point M(u,v) d'une courbe d'équation y=f(x) a pour valeur f'(u)
l'équation de cette tangente étant d'ailleurs y=f'(u)(x-u)+f(u)
on en déduit que f'(0)=-1
sachant que b=3 alors f(x)=(ax+3)e-x
d-où f'(x)=(ax+3)(-e-x)+ae-x=-e-x(ax+3-a) (rappel (eu(x))'=eu(x)u'(x))
comme f'(0)=-1 on obtient -1=3-a soit a=4
en définitive f(x)=(4x+3)e-x


