Salut Godefroy,

.

Merci pour l'énigme.

736 est un nombre autogénérateur:

4096 = 4^(0*9+6)

Bonjour,

je propose 16384 =

Merci pour l'énigme.

^{On va avoir une sacrée collection vue la largeur de recherche laissée...}

Bpnjour

si j'ai compris...

(3/1 +2)=3125 dans mon latex  5 lire puissannce

Bonjour,

Voici un nombre auto-générateur strictement supérieur à 10 et différent des exemples donnés dans l'énoncé :

343 = (3+4)^3

Merci pour cette énigme un peu trop simple !

7 + 3⁶ = 736

Bonjour Godefroy,

Pour le plaisir d'écrire en latex:

-


Merci pour la joute

Bonjour à tous et merci à Godefroy

Je n'ai à proposer qu'un exemple affreusement tiré par les cheveux:

16 777 216 (c.a.d. 16 puissance 6).

qu'on peut écrire

((((1+6+7)*7)/7+2)/1)^^6

il y a encore ici

343=(3+4)³
343=(3+4)^3
Comme beaucoup je présume.
Bonjour,
et merci Godefroy_lehardi

Pour le plaisir :
9!
362880=(3+6)!+(2+8-8)*0
26!:
403291461126605635584000000=(4*0+3+2+9+1+4+6+1)!+(1+2+6+6+0+5+6+3+5+5+8+4+0+0+0+0+0)*0

Il y a un record avec des nombres qui se suivent mais je ne le retrouve pas.
Sinon voir:

http://villemin.gerard.free.fr/Wwwgvmm/Formes/Friedman.htm

Bonjour Godefroy, et chapeau ...

(7-5+9-3+7)⁵ = 759375

Bonjour
Je propose 343 = (3+4)³
A+

343 = (3+4)³
J'avoue avoir louché sur 729
Merci godefroy_lehardi et Nicolas_75 pour cette joute.

Un peu plus compliqué :
2985984 = (2(9/8 + 5))^98/4

oups trop tard !
2985984 = (2(9-8+5))^98/4

Bonjour et merci pour l'énigme !
En voici un par exemple :



À bientôt !

Trouvé en - 10 min :

(racine de 4 )^{-2-9+4+9+6+7+2+9+6} = 4294967296

Bonjour,

Pourquoi faire simple quand on peut compliqué ? J'ai l'impression que 100! avec ses 158 chiffres en base 10 est un bon candidat:

93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000=(9+3+3+2+6+2+1+5+4+4+3+9+4+4+1+5+2+6+8-1+6-9+9+2+3+8+8+5+6+2+6+6+7+0+0+4-9-0-7-1-5-9-6-8+2-6-4-3-8-1-6-2-1-4-6-8-5-9-2-9-6-3-8-9-5-2-1-7-5-9-9-9-9-3-2-2-9-9-1-5-6-0-8-9-4-1-4
+6+3+9+7+6+1+5+6+5+1+8+2+8+6+2+5+3+6+9+7+9+2+0+8+2+7+2+2+3+7+5+8+2+5+1+1+8+5+2+1+0+9+1+6+8+6+4+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0)!


Un ptit coup d'excel, deux/trois itérations et l'affaire est dans le sac...
Je vais réfléchir un peu mais je pense que tous les n! sont autogénérateurs à partir d'un certain rang..

Merci pour cette énigme en tout cas...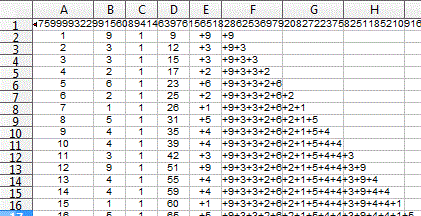

Pour reprendre la dernière question de mon post précédent
1) Existe-il une infinité de nombres autogénéraeurs en base 10 ?
2) Est-ce que les N! à partir d'un certain rang pourraient faire l'affaire pour prouver cela ?

Je pense que la réponse est "oui" aux deux questions.

N!= a₁a₂a₃a₄.... a_p00000000

En gros, une factorielle est un nombre avec des chiffres pas tous nuls sur la gauche et une ribambelle de zéros sur la droite. En effet, au fur et à mesure que N grandit, le nombre de zéros croit (démonstration plutôt facile :  nbre de multiples de 5 inférieurs à N).  

Pour trouver une forme autogénérée de N!, on va chercher à obtenir N avec une expression de la forme suivante : somme(b_i s_i) +/- 0! +/- 0! ... +/- 0! + 0 + 0 ...+ 0
avec s_i vaut -1 ou 1
et b_i=a_i si a_i<>0 ou b_i=a_i!=1 si a_i=0


Question n°1:
Est-ce que l'on arrive à atteindre N avec l'ensemble des chiffres non nuls de N ?
La réponse est "oui" car pour 100! on a déjà 158 chiffres à disposition et donc au minimum 158 x 1 (puisque on peut transformer les zéros en 1 avec 0!=1).

Question n°2
Comment arriver exactement à N avec le cumul des b_i ?
En partant de la gauche, on cumule les b_i jusqu'à dépasser N. Dès que le cumul dépasse N, on soustrait b_i. Et on continue le processus. Jusqu'à arriver dans la zones des zéros finals. Des que le cumul vaut N, on ajoute 0. Il est facile de montrer qu'à partir d'une certaine valeur de N, il y a assez de zéro en fin de N! pour atteindre N.

Je ne suis pas sûr que ça fonctionne, mais bon...

15 = ⁵_i=1 i

Merci pour cette joute !

Bonjour, voici un nombre auto-générateur strictement supérieur à 10 :

3125 = (3*1+2)^5

Bonjour,

Je propose le nombre :  

Je parie mon solex contre une rolex, que je ne serai pas le seul à proposer ce nombre ...

Bonjour Bertrand Renard !

Je propose :



Merci

Bonjour, voici le nombre que j'ai trouvé 9765625 = (9+7+6-5+6+2)⁵ . Vous trouvez que c'est un peu grand le nombre ? Moi aussi. Mais, j'ai pas eu de mal a le touver si ce n'est que le hazard ; 25⁵. Le seul effort que j'ai fournit c'est de trouver une combinaison entre les différents chiffres à part celui de l'unité pour avoir le 25. Et voilà... Enfin je remercie notre ami lehardi pour la joute.

Bonjour,

Quelques exemples:
127 = - 1 + 2⁷
343 = (3+4)³
736 = 7 + 3⁶
.....
137797 = (1 + 3⁷*7)*9 + 7
.....
jusqu'au nombre pandigital à 9 chiffres
268435179 = -268 + 4^{(3*5-1^7)} - 9 avec 1^7 = 1⁷.

Pour une grande variété de nombres auto-générateurs, voir:
http://www2.stetson.edu/~efriedma/mathmagic/0800.html

Bonjour à tous.

Ma réponse :

6495 = (6⁴ + 9) x 5

Merci pour l'énigme

bonjour
le plus simple que j'aie pu trouver est sans doute


mais il en existe beaucoup beaucoup d'autres -- plus ou moins tordus, bien sûr, par exemple




je table sur l'imagination fertile des mathiliens, qui devrait nous en faire découvrir beaucoup d'autres...

Bonjour Godefroy

Je propose       

En fait, en utilisant les puissances, il est assez facile de trouver une foultitude de solutions à cette énigme, voire des expressions de plus en plus longues :

Zut, il manque un signe puissance entre le 1 et le 0 (et non 10)

Bonjour

Je propose :

Bonjour,

Je propose


Je me réjouis de voir si quelqu'un a pu trouver une suite de nombre auto-générateurs.

Merci pour l'énigme!

(7-5+9-3+7)^5
(9+7+6-5+6+2)^5
(5*2+5*2+1*8+7)^5
(18+45+(2-8)*(1+2))^5
(50+3+2+8-4+3-7)^5
(1*1-60/2+90+6-2)^5
...

Bonjour !

Je propose

823543 = ((8-2)/3+5)^(4+3)

Merci pour l'énigme !

Ma réponse :

Bonjour

Un système avec des puissances :
262144 = 2^{(6x(2+1)+4-4))}
Merci

pardon,

Bonjour,

Je ne sais pas si la fonction exponentielle est autorisée. Au risque de me prendre un poisson, je dirais


Merci pour l'énigme.

Voilà le miens

343 = (3+4)³

Bonjour,

très inspiré du 1er exemple et (sans doute ) juste avant le gong:

16384 = ((1+6-3)^8)/4.

Merci

Clôture de l'énigme :

Je me doutais bien que le concept devait déjà exister.
C'est vrai qu'elle n'était pas très compliquée. Mais certains ont trouvé des nombres très intéressants.

Quel dommage pour Diablow Les erreurs de signes, quelle plaie !

En fait, la réponse de Diablow est juste.
C'est moi qui me trompe dans les signes.
Désolé.

Bonjour,
d'un autre cote j'avais tout fait avec excel et copier/coller donc ça n'étonnait un peu...
Merci pour cette injustice réparée

Bonjour,

Je veux juste comprendre pourquoi les nombres que j'ai proposés sont faux...
Merci d'avance pour la réponse.

@ pdiophante

C'est probablement ton nombre pandigital qui t'a valu le poisson car il ne respecte pas la consigne : 268 ne va pas, il faudrait que les chiffres 2, 6 et 8 soient utilisés individuellement.

Les autres propositions me semblent correctes, par contre.

Frenicle,

Merci beaucoup pour votre réponse.
Moralité: ne faire des excès de zèle qu'à bon escient