km.

Merci pour l'énigme !

Je trouve une longueur de 192,029 km arrondi au mètre le plus proche..

Salut godefroy,

Je propose une longueur de route d'environ 192,029 km.

Merci.

Bonjour,

La longueur totale de route à construire, sachant qu'elle doit être minimale et arrondie au metre le plus proche est: 192 029 m.

Merci pour cette joute.

Bonjour Godefroy,

Je propose : 165.711 m

Encore Merci pour cette énigme

Chaque nouvelle est attendue avec impatience par chacun d'entre nous...

A+

Bonjour Godefroy,

Les routes sont bien entendu les médiatrices du triangle, et la somme de leurs longueurs vaut environ :   192,029 km

Merci à toi pour tous ces délassements.

Bonjour
Il suffit d'ajouter les longueurs des 3 médiatrices  => = 192km
que l'on trouve avec le rayon du cercle circonscrit = 136.7919787 km et 3 fois  Pythagore
A+

Bonjour Godefroy

Je propose comme longueur totale :

192,029 km

soit 192029 m.

Cette solution est obtenue avec trois routes perpendiculaires aux côtés du triangle (22,069 + 55,561 + 114,399).

Puisque le budget de la Scalénie est en déficit, on peut faire plus court :

Il suffit de remplacer les deux routes de 55 et 114 km, par une seule, joignant le centre d'extraction au sommet commun aux côtés de 150 et 250 km.
Comme ce sommet appartient aux deux côtés, les deux pays concernés sont bien desservis.
Cette route a une longueur de 136,792 km ce qui, additionné aux 22,069 km de la dernière route fait un total de 158,161 km.

J'ai bien noté que l'énoncé parlait de 3 routes.
Deux d'entre elles peuvent-elles être confondues ?
Le ministre du budget de la Scalénie affirme que oui au nom d'une règle d'or budgétaire, inscrite dans la constitution scalène.
La société Scalroute SA, retenue dans l'appel d'offre, prétend que non, en invoquant des problèmes de sécurité et le fameux principe de précaution, qui figure lui aussi dans la constitution scalène.

La cour constitutionnelle de Scalénie, présidée par un certain Montmirail, devrait trancher dans les prochaine semaines.


Merci pour la joute

Salut godefroy !

Je trouve que la longueur minimale totale des trois routes sera de 192.029 km.

Pour le trouver, il suffit de dire que le segment le plus court entre le centre du cercle circonscrit et un côté du triangle est perpendiculaire à ce côté. Un coup de trigo, et on a le rayon du cercle circonscrit (136.792 km), et un coup de Pythagore nous donne les trois distances voulues, que l'on additionne).

A+ et merci pour l'énigme.

Bonjour Godefroy,
192,029 km ( par excès arrondi au mètre)
Merci pour la joute.

Bonjour godefroy_lehardi,

La longueur totale de route à construire est d'environ 192,029 km.

Merci pour l'énigme !

Bonjour Godefroy_lehardi

La longueur totale de route à construire est de 192029 m.
Merci pour l'énigme.

je trouve une longueur totale de 192029 m, (soit 192km et 29m).  

on trouve respectivement 22.069 + 55.561 + 114.399 (en km) pour les trois tronçons.
merci pour l'énigme !

Bonjour,

Sans chercher de vice ,les trois médiatrices devraient suffire soit 192 m.

Mais un esprit vicieux pourrait considérer qu'un angle est commun à 2 pays et dans ce cas il suffirait de deux routes totalisant 159 m pour
acheminer le métal précieux.

192 mètres

Bonjour,

Sauf erreur, la longueur totale de la route est de 192,029 Km.

Explication :
Le centre du cercle circonscrit étant à l'intersection des médiatrices, on cherche la somme des 3 médiatrices : x + y + z.

a=270, b=250, c=150, les trois cotés.
R rayon du cercle circonscrit est donné par a.b.c/2S
S surface est donnée par S = racine[p(p-a)(p-b)(p-c)]
p = demi périmètre = (a+b+c)/2

Et enfin (par Pythagore) :
x² = r² -(a/2)²  
y² = r² -(b/2)²  
z² = r² -(c/2)²

Merci WIKI ...
Et merci pour l'énigme...

bonjour,
si l est la longueur minimale :l=R(cos(A)+cos(B)+cos(C)) si R est le rayon du cercle circonscrit au triangle et A,B,C les trois angles ce qui donne sauf erreur de calcul de ma part l=192,029 km (au mètre le plus proche)

merci pour ce problème

Bonsoir,

on a trouvé de l'or au centre du cercle circonscrit au triangle ABC, territoire de la Scalénie (voir figure )



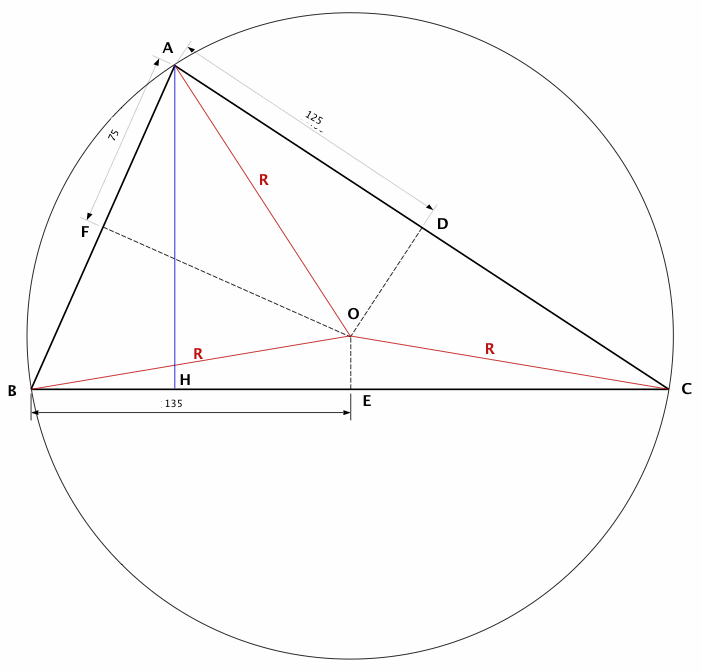
Le centre du cercle circonscrit est le point d'intersection des médiatrices des cotés du triangle. Les médiatrices étant perpendiculaires aux cotés du triangle (frontières de la Scalénie) sont donc les trajets les plus courts issus du point O vers les frontières de Scalénie : soient OD, OE et OF.
1) L'aire du triangle ABC vaut S=AH * BC / 2 mais aussi, dans un triangle quelconque,le produit des cotés divisé par 4 * le rayon du cercle circonscrit  donc S= AB*AC*BC/ 4*R

AH²=AB²-BH² et AH²=AC²-HC²; en outre BH+HC = 270 BH=270-HC  (1)
AH²=150²-BH² et AH²=250²-HC²; 150²-BH² = 250²- HC² (2)
Remplaçons BH par sa valeur tirée de (1) dans (2)
150²-(270-HC)²=250²-HC²

il vient HC = (250²+270²-150²)/540
soit HC = 209,07407
AH =(250²-(209,07407)²)= 137,06944 à partir de là, S=137,06944*270/2= 270*250*150/4*R
On obtient R= 136,79198
2) du triangle AOD on a OD =(R²-AD²⁾)^0,5
OD = 55,56118641
de même dans le triangle AFO  OF=(R²-75²)^0,5= 114,3986251
et dans le triangle BOE, OE =(R²-135²^0,5= 22,0691059
La longueur totale minimale des 3 routes à construire est donc de
OD + OF + OE = 192,0289174 km  soit arrondie au m le plus proche de 192,029 km
3) Il serait plus judicieux de rejoindre les frontières des pays voisins avec une route de trajet OE pour la frontière BC et une route commune OA pour rejoindre les frontières AB et AC.
Le trajet minimal, dans ce cas, serait alors de 136,79198 + 22,0691059 = 158,8610846 km soit arrondi au m le plus proche de 158,861 km

Amitiés, bien à vous

Il s'agissait d'une carte de la scalénie à l'échelle 1/1000°
Vous m'avez compris....

Dans le "vrai"pays j'aurais 192 km 031 ,à noter que les arrondis
bougent légèrement en fonction des choix (racines ou trigo).

Et dans le cas "vicieux" 158 km 863

Je trouve que la longueur minimale des routes à construire est de : 192.029 km (arrondi au mètre le plus proche)

Bonjour, j'ai trouvé 192 m

Salut Godefroy

Je propose une longueur de route totale égale à

192 kilomètres et 29 mètres, en arrondissant au mètre près.

En espérant que ça soit juste.

Merci pour l'énigme !

Bonjour godefroy,

ces gros jaloux de scaléniens vont devoir construire au total 192.029 km de routes.

Cordialement.

Salut,

Les distances sont de : 114.3986km ; 55.5612km ; 22.0691km
Soit un total de route à construire arrondi de 192.029 kilomètres

@++

192,029 KM
Calcul fait graphiquement

Bonjour Godefroy.
192,029 km
Dans le tableur, au début de la colonne A :
27 en prenant pour unité le myriamètre (dix kilomètres)
25
15
=RACINE(33,5*6,5*8,5*18,5) formule de Héron
=A1*A2*A3/4/A4 rayon du cercle circonscrit égale produit des côtés divisé par le quadruple de l'aire
=RACINE(A$5^2-(A1/2)^2) chaque route est le côté d'un triangle rectangle dont l'hypoténuse est le rayon de la Scalénie et l'autre côté la moitié d'un côté de la Scalénie
=RACINE(A$5^2-(A2/2)^2)
=RACINE(A$5^2-(A3/2)^2)
=SOMME(A6:A8)

À l'aide des règles pythagore et pythagore généralisé on calcul les longueur des médiane puis hauteur car la distance minimale du centre au coté est la hauteur muni de ce centre on trouve 3 longueurs ~une 48km 44km 82 km  route totale~174268m

Bonjour,

Je ne suis pas sûr d'avoir bien compris la position des routes mais je trouve 192 mètres.

Bonne soirée

Bonjour tout le monde
- Je propose 192009 mètres

Bonsoir godefroy_lehardi,

La longueur totale de route à construire est de 192,029 km.

Merci pour ces joutes géométriques.



Merci à tous ceux qui donnent des explications .
Merci à Castoriginal pour le joute 37 "les pentagones" , avec ces figures et explications mon permis de trouver mes erreurs.

192 kilomètres et un peu moins de 29 mètres.

Clôture de l'énigme :

Le résultat peut être trouvé facilement en utilisant le “théorème japonais” de Lazare Carnot, qui dit que la distance cherchée est égale à la somme du rayon du cercle inscrit et du rayon du cercle circonscrit au triangle.
Mais on peut aussi le trouver autrement.

Félicitations à totti1000 qui renoue avec la victoire après le beau doublé de frenicle (qui a trébuché ce mois-ci ).

Bravo également à castoriginal et Pierre_D qui ont réalisé un sans-faute.

Félicitations totti1000 pour ta neuvième étoile. Très belle victoire et performance, surtout au niveau de la joute poissonneuse numéro 36 avec une réponse correcte et rapide !

Merci à jamo et godefroy_lehardi pour toutes ces enigmes.

Bonjour,

Cela fait toujours très plaisir de gagner une étoile !!!

Merci Godefroy et Jun_Milan pour ces félicitations .

Bonsoir

Ben dis-donc !!! totti1000, je n'avais pas encore vu cette nouvelle victoire

Bonjour Louisa ,

et merci .

Bonjour,

Un grand bravo à toi, totti1000, pour cette belle victoire et cette neuvième étoile  

_{Je te disais bien que tout allait rentrer dans l'ordre}

Bravo Totti ; décidément, les jeunes loups sont toujours plus rapides que les vieux renards !

Bonsoir frenicle et Pierre_D ,

merci à vous pour ces félicitations, cela fait vraiment plaisir à lire !

Bonsoir

J'aime ce que tu as dit Pierre_D

Toutes mes félicitations totti pour cette nouvelle victoire bien méritée !!!
Impressionnant : aucune énigme ne te résiste... et à chaque fois, tu réussis à la résoudre en un temps record.

Du grand art !!!! .

Bonjour Nofutur2 ,

Merci beaucoup !