Niveau logiciels

La commande Enveloppe de GeoGebra.

Posté par
lake 24-12-17 à 11:48

Bonjour à tous,

  Suite à ce topic: rayon d'une famille de cercles , je m'étais mis en tête de déterminer l'enveloppe de la famille de cercles donnée, à l'aide de la commande "Enveloppe" de GeoGebra. J'ai échoué (comme d'habitude; ce n'est pas la première fois que je me retrouve en carafe avec cette commande).

En désespoir de cause, je me suis lancé dans des calculs (joufflus) pour la déterminer.

Je vous passe les détails, mais l'enveloppe en question se décompose en deux lieux:

   - Une demi-droite issue de $T_{-\frac{1}{2}}$ d'équation $y=x-1 \\$ .

   -Un courbe dont une équation  paramétrique est:

       $\begin{cases}x=\dfrac{-4m^4+8m^3-3m^2-7m+2}{2(4m^2+1)}\\\\y=\dfrac{4m^4+8m^3-m^2+7m+4}{2(4m^2+1)}\end{cases}$

Une figure:

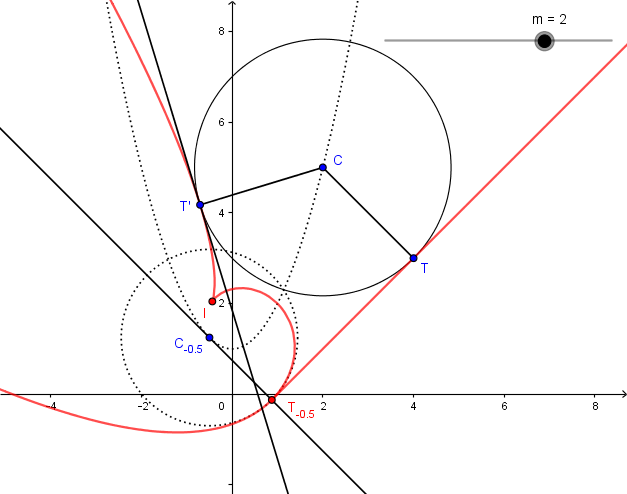
   La commande Enveloppe de GeoGebra.

Je poste ces détails pour bien montrer ce que je voudrais obtenir à l'aide de la commande "Enveloppe" de GeoGebra (la courbe rouge).

La commande "Enveloppe" a pour arguments un "chemin" et un "point". Il faut, en l'occurrence, déterminer les cercles de la famille de manière "géométrique" (par exemple un lieu pour le centre et un point du cercle). J'ai fait de multiples essais: en vain.

En désespoir de cause, je suis allé me renseigner sur le forum GeoGebra.
Vous pouvez voir la discussion ici:

Noël Lambert, qui n'est pas le premier venu dans le monde GeoGebra, ne me laisse guère d'espoir et je commence à douter d'une possibilité de réussite. Vous pouvez voir entre autres sa dernière réponse où il a généré les cercles de la famille de manière astucieuse (fichier EnvMoi.ggb) mais sans résultats.

Peut-être l'un d'entre vous aura-t-il une idée lumineuse ?

Merci de m'avoir lu

Posté par re : La commande Enveloppe de GeoGebra. 24-12-17 à 12:00

J'ai oublié:

Joyeux Noël à tous!

Posté par re : La commande Enveloppe de GeoGebra. 24-12-17 à 12:57

salut,
je ne sais pas si ceci est interessant ?
Avec Xcas:

eq:=x^2+y^2-2m*x-2y*(m^2+1)+(m^2+2)*(m^2+2m-1)/2
enveloppe(eq,m)
parameq(enveloppe(eq,m))

Posté par re : La commande Enveloppe de GeoGebra. 24-12-17 à 13:33

Bonjour alb12,

Effectivement, Xcas fonctionne sans difficultés sur ce coup là.

Mais j'aimerais bien m'en sortir avec la commande Enveloppe de GeoGebra.

Posté par re : La commande Enveloppe de GeoGebra. 24-12-17 à 13:49

Bon, je crois que j'ai ma réponse sur le forum GeoGebra; les gens intéressés peuvent cliquer sur le lien donné à 11h48 et lire la réponse de Michel Iroir.

Posté par re : La commande Enveloppe de GeoGebra. 24-12-17 à 16:02

Bonjour,

j'ai essayé tout ça

ça finit par marcher mais c'est vraiment bien trop dépendant de la façon dont est définie la parabole lieu du centre ...
(heureusement dans l'exo en question on n'en demandait pas tant !! activer la trace du cercle et "regarder" suffisait)

Posté par re : La commande Enveloppe de GeoGebra. 24-12-17 à 16:26

Bonjour mathafou,

  Je suis d'accord du tout au tout:

    - La commande Enveloppe de GeoGebra n'est pas vraiment une panacée même dans le meilleur des cas

     - Et oui, l'exo en question est loin de tout ça; c'est la raison pour laquelle j'ai créé ce topic ...

Je voulais m'amuser et ma foi, j'ai passé un bon moment grâce à lui

Très bonnes fêtes!