Inscription / Connexion Nouveau Sujet
le Pentagone de Sin Pan
Sin Pan avait demandé à l'empereur de Chine ( de la dynastie des Ming bien sûr ) un vaste terrain pour y construire une académie de géométrie.
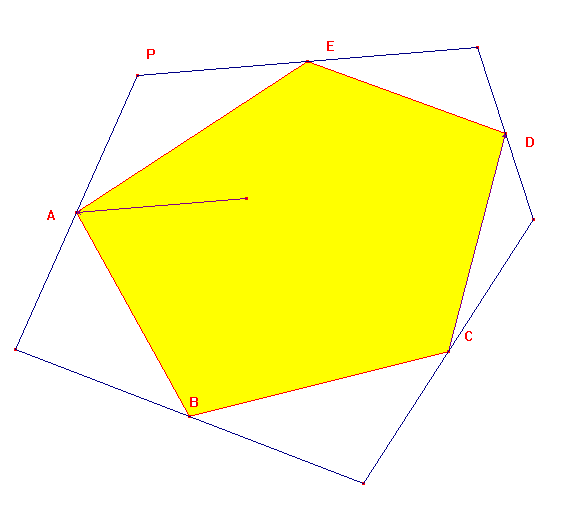
Voulant s'assurer qu'il avait à faire à un vrai géomètre, l'Empereur dit à Sin Pan:" Je dispose d'un terrain en forme de Pentagone. J'ai fait marquer par cinq bornes, les milieux de ses côtés. Trace les limites de ce pentagone et il est à toi."
Comment Sin Pan procéda-t-il?
Bonjour
Si je comprend bien ,il s'agit du milieu des cotés du pentagone virtuel à retrouver
 Cliquez pour afficher
Cliquez pour afficherBonjour,
considérons la figure ci-dessous:
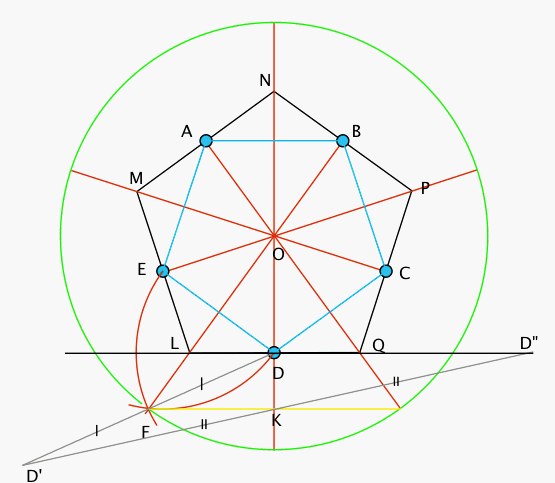
les bornes données par l'empereur sont les points bleus A,B,C,D,E qui sont les
milieux des côtés du pentagone cherché. On relie ces bornes deux à deux (segments en bleu sur la figure). En prenant un compas,on peut construire le point F, intersection des arcs de centres E et D et de rayon DE. En joignant F à B, on construit la médiatrice de DE qui passe par le centre O du pentagone à construire. On répète cette opération pour chaque borne.L'intersection des médiatrice fixe le point O.On peut tracer un cercle de centre O et passant par F et les autres points d'intersection des médiatrices avec ce cercle ( en vert). Ces points sont les sommets d'un pentagone homothétique de celui recherché. Pour tracer le côté du pentagone cherché dont le côté est parallèle à FKG (en jaune)et qui passe par D, on utilise la propriété de la droite des milieux. On trace D' symétrique de D par rapport à F sur la droite DF et le point D", symétrique de D' par rapport à K sur la droite D'K. On trace la droite D"D qui coupe les médiatrices en L et Q: le côté du pentagone cherché est LQ. On trace un arc de cercle de centre Q, de rayon LQ qui coupe la médiatrice suivante en P.
De proche en proche on trouve N,M. Le pentagone cherché a pour sommets L,M,N,P,Q
Bien à vous
Bonjour
Une précision pour dpi et castoriginal, l'énoncé ne précise pas que le pentagone est régulier.
A+