Inscription / Connexion Nouveau Sujet
juste une remarque en passant (et avant d'aller couper du bois) et pour unifier certain résultats :
L'inégalité peut se réduire à :
sachant que a et b sont positifs ...
Le problème quand on balance des exercices sans les avoir vraiment cherchés c'est qu'on ne sait pas sur quoi on va tomber . Quand en plus on n'est pas vraiment disponible ...
Le cas général semblant plutôt lourd et de peu d'intérêt , je propose un compromis entre les différentes propositions :
On ne considère que des rectangles à côtés entiers et on cherche le périmètre ( l'aire ) du plus grand équitriangle inscrit dans ce rectangle . Le cas du triangle réalisant la moitié de l'aire du rectangle est déjà résolu mais pour les autres cas le problème reste ouvert : un critère donnant la position du triangle réalisant le maximum et si possible son aire en fonction des côtés du rectangle .
Imod
PS : merci aux participants qui ont accepté de me suivre et désolé pour ma participation en pointillés .
PPS : Un argument pour confirmer l'hypothèse de LittleFox concernant les deux sommets communs au rectangle et au triangle ?
PPPS : je serais bientôt pleinement avec vous , bonnes vacances à ceux qui ont cette chance 
Bonjour,
J'apprécie que mon terme d'équitriangle ait été "homologué" faute de mieux .
Je suis d'accord avec ta définition de recherche.
C'était une idée intéressante ;tout à fait dans l'esprit "détente"
Attention , les points ne sont pas sur les courbes mais entre elles ( au sens large ) . Les solutions sont 5X9 , 5X10 , 5X11 , 5X12 , 6X7 et 6X8 . Les calculs sont simples et on trouve au passage un deuxième triangle rectangle ( le double du fameux 345 ) .
Il reste à démêler les autres cas 
Imod
Après analyse des bornes et comparaison des solutions, j'obtiens que la solution avec un côté confondu avec une diagonale est toujours meilleure que celle avec un sommet sur le côté adjacent.
Donc si on reprend le graphe de Imod
Même s'il reste des points à éclaircir , il me semble que pour les rectangles à côtés entiers réalisant la moitié de l'aire , les six solutions sont données par la double inégalité de LittleFox
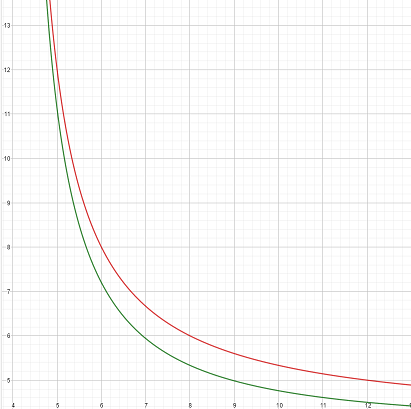
Imod
Il n'y a pas de courbe supplémentaire, le quadrant est divisé en 3 zones:
- Sous la courbe
- Entre cette courbe et la courbe
- Au dessus des deux courbes, la solution utilise la diagonale et est
Note: sur la deuxième courbe, les trois solutions ont la même valeur.
Et pour reprendre l'unification de carpediem:
Il y a une solution si
Si , cette solution est
, sinon elle est
Autre observation:
8 x6 donne la solution la plus "entière" comme l'a noté Imod avec A=P=24= 6x8x10
suivi de 12x5 -->5x12x13
2 autres donnent des dimensions à faibles décimales 6.5x7x7.5 6.25x7.25x9 .
Par contre 10x5 n'est pas évident: 5.26392012 ..x9.736068.. x10.
J'ai essayé un carré 7X7 : impossible donc de trouver 24.5 mais j'ai un maxi à 23.666
soit à 96.6%.
Rares sont le solutions à +90 % comme notre fameux 10x6.
@Dpi pour 10X5 et 11X5 , il suffit de couper la longueur en et
. La solution est facile à trouver en remarquant qu'il y a une symétrie par rapport à la longueur .
Imod
La dernière synthèse de LittleFox est vraiment simple et cohérente avec l'ensemble des résultats obtenus ( il y a une inversion dans l'inégalité avec 1/2 ) .
Je n'ai pas compris la note :sur la deuxième courbe, les trois solutions ont la même valeur.
Tout n'est pas complètement justifié mais je suis très confiant .
Bravo à tous , je ne voyais pas une conclusion aussi synthétique 
En plus la solution est constructible à la règle et au compas comme au temps de grand-papa .
Imod
Bonjour et merci pour l'animation
En marge de ce débat passionnant je me suis amusé à inscrire un "équitriangle" isocèle dans un rectangle de 6 par 8. Si cela tente quelqu'un .....
Bonjour dpi
Je n'arrive pas à trouver le configuration qui permet d'obtenir A =P = 22,6....
j'en suis à A= P = 21,93.... avec cette configuration
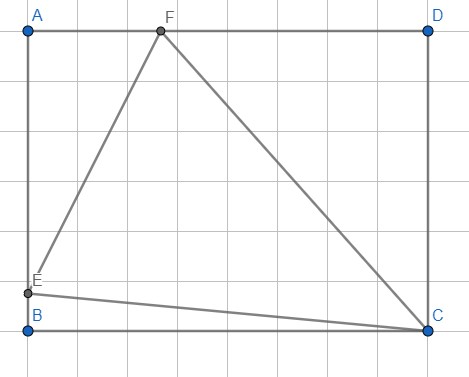
Personnellement je suis toujours sur le problème initial dont j'essaie de justifier la solution "proprement" . La solution générale donnée par LittleFox est extrêmement simple mais passe par des calculs un peu ardus . En bref peut-on expliquer le résultat plus simplement .
J'ai essayé de prendre le problème à l'envers : on part d'un équitriangle et on cherche à l'inscrire dans un rectangle le plus petit possible . Tout de suite deux questions se posent : comment dessiner simplement un équitriangle et qu'entend-on par plus petit rectangle ?
En fait la réponse à la première question est complètement évidente , ce sont les triangles dont le rayon du cercle inscrit vaut 2 . On retrouve au passage une justification à la limite inférieure de la largeur .
La réponse à la deuxième est moins claire , disons qu'il y en a plusieurs correspondant aux situations suivantes :


Je ne sais pas si cette approche peut apporter quelque chose d'utile .
Imod
C'est peut-être évident mais je ne l'aurais pas vu 
Ça apporte de nombreuses simplifications 
Trois possibilités:
- En mettant le cercle tangent au milieu d'un grand côté du rectangle, le triangle déborde du rectangle: Il n'y a pas de solution.
- Sinon, en mettant le cercle dans un coin du rectangle, le triangle déborde du rectangle: Il y a une solution intermédiaire où le triangle est juste sur le côté opposé et la solution vaut la moitié de l'aire du rectangle.
- Sinon, la solution est trouvée en mettant le triangle sur une diagonale et le cercle contre le petit côté du rectangle.
C'est amusant de croiser les points de vue , je n'avais même pas remarqué que le cercle se baladait sur la longueur du rectangle 
Imod
@LittleFox
Après relecture à tête reposée de ton dernier message , je me suis rendu compte que je n'ai rien compris 
J'ai toujours eu le cerf-volant  .
.
Il y a un triangle dont le rayon du cercle inscrit vaut 2 et un rectangle . Si on impose le triangle , le cercle qui va avec s'appuiera sur un côté ou une diagonale du rectangle , ça c'est clair . Mais pour "le" ou "les" plus petits rectangles enfermant le triangle ....
Ce qui me gène c'est que tu considères à la fois que le triangle et le rectangle sont donnés .
Imod
Je considère que le rectangle est donné. Pas le triangle.
Pour un rectangle donné, il n'y a que deux triangles à considérer (et leur symétries).
- Soit le triangle a un côté confondu avec un grand côté du rectangle et le sommet opposé est sur le grand côté opposé. Le cercle est tangent à un grand côté du rectangle.
- Soit le triangle a un côté confondu avec une diagonale et le cercle est tangent à cette diagonale et à un petit côté du rectangle.
On peut remarquer aussi que le triangle avec la plus petite hauteur tout en ayant un côté confondu avec un grand côté du rectangle est obtenu en mettant le cercle au milieu du grand côté. Si cette hauteur est plus grande que le petit côté, alors il n'y a pas de triangle possible.
D'un autre côté, si on part du triangle (dans ce cas le triangle est donné, pas le rectangle):
Si celui-ci est aigu, alors seule la solution avec le plus grand côté du triangle confondu avec un grand côté du rectangle est possible.
S'il est obtus, alors les deux solutions sont possibles et il faut définir ce qu'on entend par plus petit rectangle 
En relisant le fil je me suis rendu compte que rien ne justifiait que le triangle devait partager deux sommets avec le rectangle . J'ai essayé de le démontrer mais je ne suis arrivé qu'à un sommet dans l'angle et deux sommets sur les côtés : il doit me manquer un argument 


Je sais que le sujet date un peu mais j'adore fouiller dans les archives 
Imod
Je ne suis pas à l'aise avec geogebra mais si tu fais monter le cercle le long de (HE) en écartant les côtés du triangle beige , tu ne dépasses pas l'aire du triangle vert ?
Imod
L'aire du triangle vert est maximale puisqu'elle est égale à la moitié du rectangle.
Il y a peut-être une solution de même aire mais symétrique par rapport à HE.
Je vais essayer 
La réponse est non 
Le triangle mauve déborde avant que MN soit la diagonale du rectangle.
L'aire est inférieure au maximum (de pas beaucoup, certe ^^).







