Ewendoun, bonjour
pourrais-tu renseigner ton profil s'il te plaît (choisis dans la liste ce qui te coreespond le mieux, reprise d'études ? ou ...)
Je te remercie

extrait de la FAQ du forum :

Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau sujet ?

Oui, indiquer son niveau (dans son profil) et celui du problème est obligatoire lorsqu'on pose une question.

Un correcteur pourra ainsi facilement juger s'il est en mesure de vous aider ou non. En l'absence de cette précision, aussi bien sur votre profil que sur le forum dans lequel le sujet est publié, il risque moins de vous indiquer une méthode que vous n'avez pas encore vue en classe, etc.

De même, si vous êtes élèves dans un pays francophone, vous pouvez consulter les équivalences des systèmes de niveaux scolaires afin de choisir le niveau de la classe française correspondant à votre classe. Cela permet au correcteur d'intégrer le fait que votre niveau scolaire ne correspond pas forcément à celui stipulé dans les programmes français en vigueur.

Il est de même demandé aux aidants de renseigner leur profil, ce qui en général donne une bonne indication du niveau de l'aide apportée.

Bonjour,

Toutes mes excuses, je n'avais jamais bien pris en compte l'importance de la précision du niveau d'études (hétérogène me concernant) dans mon profil ni dans un post forum. Voilà qui est fait.

Je ne sais précisément de quel niveau exact cet énoncé ressort, pour être honnête il a été lancé en tant que défi stimulant, et de fait je suis pour le moment bien en peine de savoir comment procéder. A priori vu le groupe dont il est issu, cela doit être un petit défi lancé à des élèves de terminale francophone, en 2016 (seule note fournie sur l'énoncé). J'aime ces problèmes posés qui ont l'air tout simples, mais qui en fait remuent beaucoup les méninges (enfin à mon humble avis et niveau).

Merci à vous chers et chères membres de cette communauté mathématique de vous pencher dessus, je m'y casse les dents pour le moment, mais suis coutumier du fait de passer à côté de choses évidentes pour des matheux plus avisés ou expérimentés.

Bien à vous !

Ewendoun

Bonjour,

cette inégalité est vraie pour tout x, y et z réels strictement positifs tels que xyz = 1.
on peut poser z en paramètre, en déduire y fonction de x et de ce paramètre :
Dériver la fonction pour voir que la dérivée n'a qu'une seule racine réelle positive,
vérifier que la fonction est bien maximale et <= 1/2 pour cette racine.

Bon courage....

Merci beaucoup de votre réponse

Bonsoir,

la démarche que j'ai proposée n'est pas une vraie démonstration
Elle n'est pas satisfaisante, bien que fort instructive...
Quelqu'un a certainement une vraie démonstration !

La réponse fournie pour le moment me satisfait, par ailleurs l'énoncé précise seulement "montrez" ce qui souvent en langage énoncé mathématique lycée (enfin de mémoire versus "démontrez" ) demande de parvenir au résultat énoncé dans l'exposé du sujet plutôt que de produire ou élaborer une réelle démonstration.

Je crois comprendre le sens de la réponse, pourtant je vois mal comment poser z en paramètre pour en extraire y en fonction de x. J'admets être plutôt limité en maths, mais un bon exemple (?) pas forcément celui de l'énoncé d'ailleurs, peut m'aider à comprendre la manip ? Je sais à peu près pour exemple pratiquer des changements de variables, mais là je butte sur la façon de procéder ?
Merci encore

Bonjour,

Eh bien après avoir discuté avec le professeur de mathématiques qui a posé ce qui est bien un petit "défi" à ses étudiants de terminale (il aime pousser le niveau !), je ne sais si la résolution du problème consistant à montrer la validité de l'inéquation peut se faire précisément avec les outils que tu envisages cher @Vham, mais sa méthode a le mérite de reposer uniquement sur une sorte de paramétrage et de mise en système des éléments de gauche de l'inéquation, j'admets avoir été soufflé, pas de dérivée ou autre, juste du "jeu" de simplification et identification terme à terme, ce qui en théorie est accessible à tout étudiant de fin de lycée !

Bon, pour conclure, je vous poste bientôt la résolution complète du problème énoncé si cela vous intéresse, personnellement ma curiosité - et mon ego, je l'admets :p ) - a été quelque peu piqué au vif. Oui, je suis facilement en tant qu'éternel novice en mathématiques (et en bien des choses) aisément impressionnable.

Merci en tous cas de votre aide et de l'intérêt porté à ce petit tour de magie mathématique.

Ewendoun

Bonjour,

Pour se débarrasser de la contrainte , on peut poser:

  

J'avais tenté quelque chose dans ce sens mais malheureusement pas abouti...

Bonjour,

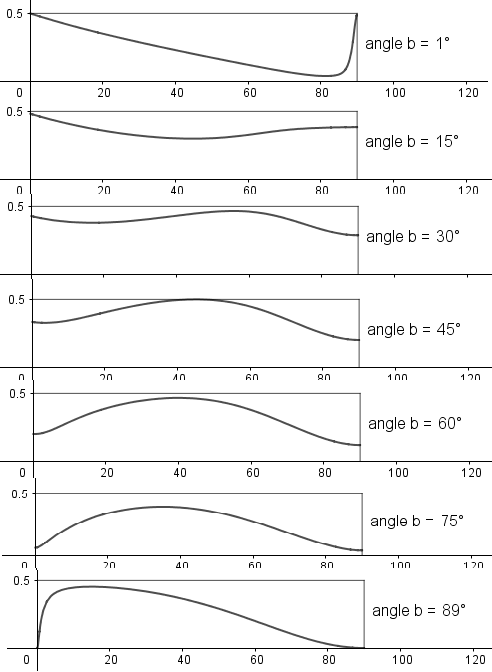
pour "montrer" je pose x=tan(a), y=tan(b) et z=1/(tan(a).tan((b))
et j'utilise GeoGebra de la façon suivante :
je crée un curseur "angle b" qui peut varier de 0 à 90 (en degrés)
et je visualise la fonction "membre de gauche de l'inéquation" en ayant l'angle a en abscisses, lui aussi de 0 à 90 (en degrés).
le curseur "angle b" paramètre la courbe tracée en ayant mis en bijection les entiers de 0 à l'infini avec les angles de 0 à 90.
Visualisation très efficace reproductible facilement par un lycéen.

re bonsoir

en attendant la résolution du tour de magie, voici mes visualisations :

salut,
un graphe 3d

Oui, bien sûr, que l'inégalité d'Ewendoun soit vraie, tout le monde en est convaincu. Mais pour l'instant, même avec des graphes qui confirment la chose,  je ne vois rien de probant.

Bonjour,

Donc pas de piste pour une démonstration.

Bonjour, j'ai la solution de ce "défi" mathématique, mais cela prend trois plombes à mettre en forme sous latex, à moins que je puisse copier la solution sous forme d'image exceptionnellement ? Merci encore à tous et toutes

Bonjour à tous
allez, je vais dire oui, si tu l'as sous forme de pdf pour lequel tu pourrais mettre un lien ce serait bien, ou envoie le moi sur mon mail (dans mon profil)

Bonsoir,

-> Ewendoun : Avec le principe de la solution, et une piste s'il y a une astuce, nous serions peut-être capables de détailler par nous-mêmes ?
Sinon, pour écrire "facilement" en Latex sur ce site, utiliser l?icône LTX juste à gauche de dans la barre d'icônes sous la zone de réponse

malou edit

Bonne nuit,

Je suis toujours intéressé par une démonstration
qui peut m'être transmise via mon E-Mail (tout document ou image)

On piaffe d'impatience

Bonsoir,
Nous restons sur notre faim

Bonjour,

Ewendoun a écrit : j'ai la solution de ce "défi" mathématique,
peut-être s'est-il trop avancé ? Peut-être verrons-nous après lès vacances ?

ouais on attend toujours ...

_{Voici le pdf de la correction : (malou edit : j'ai rapatrié le pdf sur notre site)}

Toutes mes excuses pour le délai monumental, voici la résolution proposée par le professeur de mathématique à l'initiative du défi. Pour ma part, j'admets que je n'y eus pas pensé, après je trouve cette approche chouette en soi car requiérant peu d'outils et compréhensible en soi assez aisément, mais dure à amorcer (pour ma part je m'y suis cassé les dents ) !

Bien à tous et toutes chers îliens et îliennes !

Ewendoun

_{* Modération > Lien accepté exceptionnellement   *}

Mieux vaut tard que jamais
Une piste pour ceux qui veulent encore chercher un peu, associée à une remarque :
En notant T le premier membre, on commence par démontrer T (1/2)S

où
Puis on démontre S = 1 par ce qui semble un tour de passe passe.
Mais démontrer S = 1 peut se faire sans astuce.
Il suffit d'y remplacer z par 1/(xy)

Bonjour,

C'est tellement simple qu'on en reste pétrifié !
Après avoir tourné autour du pot, bien sûr : x^2+y^2-2xy =(x+y)^2 toujours >= 0

pardon,  x^2+y^2-2xy =(x-y)^2 toujours >= 0

ce n'est pas un tour de passe-passe ni une astuce c'est uniquement l'utilisation pertinente de l'hypothèse : xyz = 1 ... (il faut bien s'en servir à un moment !!!)

donc que



c'est ce que j'avais tenté vainement car n'avais pas vu qu'il fallait d'abord faire une majoration pour arriver à ce S ...

La notion de "tour de passe-passe" ou de "astuce" est subjective...
Dans le pdf du lien, la démonstration de S=1 fait croire à ce que je dénomme ainsi.
Alors que je la trouve bien compliquée.
C'est tout

oui moi aussi

mais dans tous les cas c'est l'utilisation de l'hypothèse d'une façon ou d'une autre qui permet de conclure ...

Un petit bonus :
Il est facile de prolonger pour prouver que l'égalité n'est réalisée que pour x=y=z=1.

Bonjour à tous
merci à Ewendoun d'avoir pris le temps d'écrire un fort joli message dans notre livre d'or.
Bonne journée à tous

Et aussi de nous avoir soumis cette inégalité qui nous a longuement résisté

Bonjour,

De rien et de rien , c'est vrai dans les deux cas. Le mot dans le livre d'or me semblait un minimum pour louer les bienfaits du site, et ce petit jeu mathématique était bluffant par la simplicité de sa réponse, mais et cela vaut pour moi, encore fallait-il mettre le doigt sur deux trois spécificités de "tournures".

Evident a posteriori, à s'en frapper le front du plat de la main, pourtant impossible de dénicher le coeur de la résolution seul pour ma part.
Honnêtement j'avais mis un bout d'ongle sur le début, mais à un moment, je n'aurais pas pensé à tourner le problème comme cela. Du coup c'est un peu amusant et magique car c'est le genre de moment où je me dis : "Bon sang, bien sûr !" et même si a priori ça ne "sert" pas à grand chose en soi, eh bien ça participe de la beauté des maths, où on peut aussi faire des choses rigolotes avec somme toute des outils très simples.

Personnellement, j'irai creuser du côté de ce professeur, en lui demandant si il a d'autres "énigmes/riddles" de cet acabit. Avec sa permission, je vous les partagerai aussi ? En postant dans une section dédiée peut-être ?


Bien à vous tous et toutes

Ewendoun

reBonjour
Tu peux poster ce genre de choses dans "détente / énigmes ou exercices "
bonne journée

il aurait suffi de donner une piste sans rien devoiler:
minorer a^2+b^2

J'ai essayé de ne pas tout dévoiler dans mon message d'hier à 12h13.
Mais ce que tu proposes, alb12, aurait sans doute été plus judicieux.

je remarque que si le posteur dit que l'exercice est difficile alors on a du mal à trouver
on a tendance à se dire que c'est du niveau olympiades et on cherche trop haut
comme le dit Sylvieg la demo tient en 3 lignes

@alb12 et Sylvieg

Toutes mes excuses, je tenais à partager à cette communauté ce petit "défi" donné sans autre indication à l'origine que l'énoncé initial, ce qui en fait aussi le miel et le sel je pense ?

Je n'avais par ailleurs pas la solution avant un temps certain, avant qu'on me la fournisse, et j'admets volontiers que je n'aurais pas trouvé seul de mon côté. La prochaine fois, si un autre de ces "défis - le terme est un peu excessif effectivement, quoique ?-me parvient, je tâcherai de réfléchir sur des pistes plutôt que de fournir d'emblée la solution , ça pimentera plus le jeu de recherche et d'essai personnel.

C'est vrai, on pouvait faire plus court sans doute (quoique là la résolution est complète à tout le moins), toujours est-il que ça ne me semblait pas simple d'emblée.
En somme un effet psychologique qui aurait empêché la bonne intelligence de chacun de fonctionner ? Je ne sais pas, peut-être, le prochain si j'en ai un sous la main, je le posterai en indiquant rien de particulier sur la difficulté présumée (ou alors, pus rigolo, en mentionnant sa facilité ? )

Bien à vous tous et toutes,
Une excellente soirée.

Ewendoun

@Ewendoun,
Il est clair que nous sommes contents que tu aies eu la bonne idée de nous soumettre ce "défi".
Et nous nous réjouissons de la perspective d'en avoir d'autres à nous mettre sous la dent.
En postant dans le forum détente, il y a une fonctionnalité de "blankage".
On peut cacher ses réponses.
Ceux qui veulent la regarder peuvent ouvrir.
Ceux qui veulent continuer à chercher n'ouvrent pas.
Je te conseille d'aller jeter un oeil dans cette partie de l'île