Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Produit scalaireTopics traitant de Produit scalaire [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

opération produit scalaire

Posté par
Eye 26-01-11 à 12:45

Bonjour, je viens de commencer les produits scalaires et j'ai un exercice à faire et je ne sais pas comment le résoudre
nous avons u et v deux vecteurs.
LA NORME de u =3 et celle de v= 2
le produit scalaire de u et v=_3

on doit calculer (3U-2V)2

ET (4u-3v). (u+2v)

svp expliquez-moi comment on fait parce qu'on doit prendre en compte le carré et k...

Posté par
dhaltere : opération produit scalaire 26-01-11 à 12:46

Revois tout simplement tes notes de cours sur les opérations possibles dans les calculs de produits scalaire.

Posté par
dhaltere : opération produit scalaire 26-01-11 à 12:47

Euh, c'est quoi, k ?

Posté par
Eyere : opération produit scalaire 26-01-11 à 12:55

Le problème c'est que nous venons à peine de commencer et nous avons juste marqué que (ku).v=k(u.v)
je pense que k est le réel multiplicateur

Posté par
dhaltere : opération produit scalaire 26-01-11 à 14:13

Bof, voilà les réponses.
Je ne sais si tu es sincère ou pas.
N'avoir vu que la linéarité par rapport au produit externe et pas les autres relations, et avoir un exercice aussi basique à faire, ça me titille.

3$||\vec u||^2=\vec u.\vec u = 3^2 \\ ||\vec v||^2=\vec v.\vec v = 2^2 \\ \vec u.\vec v = 3

Et ne viens pas me dire que 3$\vec u.\vec v=-3
(relis-toi d'abord)

Alors soit à calculer la quantité A ci-dessous :
3$A=(3\vec u-2\vec v)^2

On utilise la distributivité, qui suit les mêmes règles que pour les produits de réels
3$A=(3\vec u-2\vec v).(3\vec u-2\vec v)
3$A=(3\vec u).(3\vec u)-(2\vec v).(3\vec u) - (3\vec u)(2 \vec v) + (2\vec v)(2\vec v)
On utilise la linéarité de la multiplication externe [la règle que tu cites : (ku).v=k(u.v) ]
3$A=3^2(\vec u).(\vec u)-3\times2(\vec v.\vec u) -3\times2(\vec v.\vec u) + 4(\vec v)(\vec v)
On utilise la commutativité du produit scalaire (3$\vec v.\vec u=\vec u.\vec v) et la factorisation
3$A=3^2(\vec u).(\vec u)-12(\vec u.\vec v) + 4(\vec v)(\vec v)

Avec les règles que j'ai évoquées sur les normes de vecteurs, on a
3$A=9||\vec u||^2-12(\vec u.\vec v) + 4||\vec v||^2

Et en remplaçant par les valeurs numériques :
3$A=9\times3^2-12\times3 + 4\times2^2

Tu sauras terminer le calcul ?

Fais la suivante seul, ça me réjouira.

Posté par
Eyere : opération produit scalaire 28-01-11 à 21:54

Merci beaucoup de ton aide.
Oui je suis sincère je ne vois pourquoi je ne le serais pas .
Alors je trouve -3 pour la deuxième. Sur mon livre de maths u.v= -3

Posté par
dhaltere : opération produit scalaire 29-01-11 à 10:22

Je pose simplement la question de la sincérité parce que je ne te connais pas, et qu'il me semble que l'argument d'un cours incomplet et d'élèves lâchés dans l'arène des fauves sur des exercices impossibles est souvent utilisé.
Mais je veux bien te croire...


Je me doutais que ta notation initiale _3 pouvait s'interpréter comme -3.

Si tu veux un conseil (que tu vas peut-être interpréter comme une critique), apprends à te relire.

Donc avec 3$\vec u.\vec v=-3, tu as du trouver
3$(3\vec u-2\vec v)^2=133

Maintenant, effectivement,
3$(4\vec u-3\vec v).(\vec u+2\vec v)=-3

Tu vois, même sans avoir vu les règles en cours, tu as su trouver la bonne réponse.

Tiens, un beau graphique pour visualiser les différents vecteurs impliqués dans cet exercice
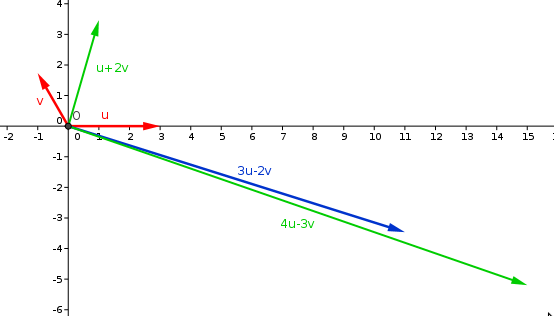
opération produit scalaire

Deux, trois petites remarques, comme ça, si par hasard tu ne les vois pas en cours...
3$(3\vec u-2\vec v)^2 est le carré de la longueur de la flèche bleue.
3$||\vec v||^2=(\vec v)^2=2^2 est le carré de la longueur de la flèche rouge marquée "v".

Une fois que j'ai choisi le vecteur 3$\vec u, ce qui est tout à fait arbitraire, le système d'équations
\{||\vec v||=2 \\ \vec v.\vec u=-3
permet presque de définir le vecteur 3$\vec v :
il y a deux positions possibles pour 3$\vec v
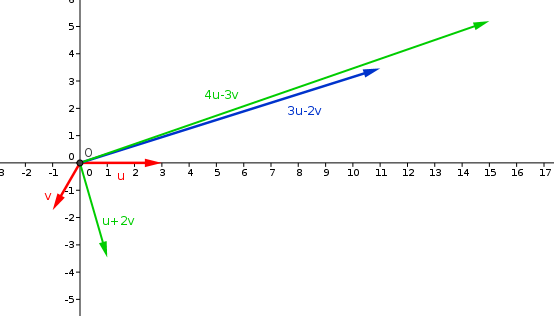
opération produit scalaire

Ces deux solutions sont symétriques par rapport à la direction donnée par 3$\vec u

Si tu veux réviser comment trouver sur le graphique ces deux solutions, n'hésite pas à poser la question.


Rechercher
Menu
Espace membre
23 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1719 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !