Inscription / Connexion Nouveau Sujet
Optimisation
Bonjour, j'ai ce DM à faire et je bloque... Pourriez-vous m'éclairer s'il vous plaît?
Une boîte en carton rectangulaire de 8 décimètre sur 10dm, en découpant quatre carrés identiques, on obtient le patron P(x) d'une boîte sans couvercle (voir schéma).
1)Quelle est la plus grande valeur de x possible? Comment avez vous déterminé cette valeur? Quel est le volume de la boîte pour cette valeur déterminée? Pour cette valeur trouvée, comment est le patron P(x)? A votre avis, ce volume peut-il être le volume maximal cherché? Argumentez
Voici ce que j'ai fait mais je ne suis pas sûre que ce soit correct:
x= 2
10-4=6 -> V= 6x4x2 = 48dm3
8-4=4
x = 3
10-6= 4 -> V= 4x2x3 = 24dm3
8-6=2
x=1 -> V= 8x6x1= 48dm3
x=0,5 -> V= 9x7x0,5 = 31,5dm3
x=1,5 -> V= 7x5x1,5 = 52,5dm3
2) Quelle est la plus petite valeur de x possible? Comment avez-vous déterminez cette valeur? Quel est le volume de la boîte pour cette valeur? Pour cette valeur trouvée, comment est le patron P(x)? A votre avis ce volume peut il être le volume maximal cherché?
3) En fonction de x, exprimez l'aire du fond de la boîte A(x) (partie hachurée). Développez la formule A(x) que vous avez trouvée et réduisez-la. Déduisez, alors, le volume V(x) de la boîte en fonction de x.
Merci d'avance.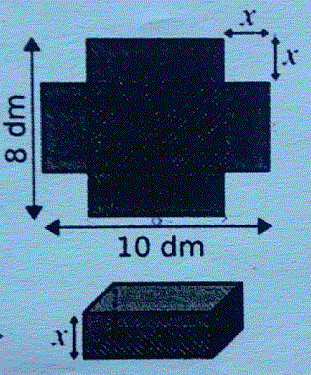
Bonjour, je crois l'avoir déjà fait en première, tu peux voir que sur ton schéma un des côtés de ton rectangle vaut 8 dm même si cela est absurde c'est la plus grande valeur de x, tu ne peux pas prendre 10 car pour la largeur ce serait une mesure négative. Cela ne peut pas être le volume maximal recherché car la boite sera toute petite et il n'y aura pas de largeur( car 8-8=0)
Donc d'après ce que je t'ai dit qu'elle est la plus petite valeur de x ? 
Bonjour,
Quelle est la plus grande valeur de x possible?
Pour répondre à cette question, regarde ce qui se passe quand x augmente.
Tu vois que la largeur du fond qui vaut 8-2x diminue , de même que la longueur (10-2x).
Ces quantités doivent rester positives, sinon cela n'a plus de sens.
x=4 est la limite maximale, la hauteur de la boîte est alors maximale mais le fond a une aire nulle, le volume est nul, ce n'est plus vraiment une boîte.
Même type de raisonnement pour x minimum.
Une longueur x est forcémént positive ou nulle...
Que se passe-t-il si x=0 ?
Le fond a pour dimensions l=8-2x et L=10-2x
A=L*l
A(x)=(8-2x)(10-2x)=....à développer puis réduire
V(x)=A(x)* x (volume du pavé)


