Bonjour tout le monde!!

j'ai un devoir maison à rendre pour la rentrer c'est en spé.maths cependant je ne sait vraiment pas comment y procéder surtout pour la question 1.a qui est l'ouverture du DM...
Svpl j'ai grand besoin de lumière..

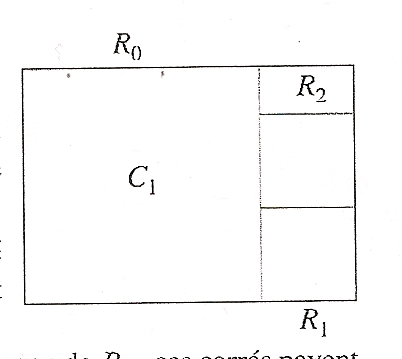
1) Soit un rectangle R0 de dimensions 21 et 15 cm. On se propose de paver ce rectangle par des carrés de même côté a, c'est-à-dire de recouvrir exactement ce rectangle par des carrés de côté a.

a. On construit un carré C1 de côté 15 cm intérieur au rectangle R0 comme sur le dessin ci-contre : ce rectangle R0 est alors partagé en C1 et en un nouveau rectangle R1. Montrer que, si des carrés de côté a conviennent pour le pavage de R0, ces carrés pavent C1 et donc aussi R1.

b.On construit deux carrés identiques C2 et C'2 de côté le plus grand possible à l'intérieur du rectangle R1 :
R1 est alors partagé en deux carrés et un nouveau rectangle R2.
Montrer que, si des carrés de côtés a conviennent pour le pavage de R0, ces carrés pavent aussi C2, C'2 et donc R2.

c. On constate alors que l'on peut paver le rectangle R2 avec des carrés : quelle est la taille maximale de ces carrés ? Ces carrés pavent-ils R0 ?

d.La détermination de R1 provient de l'égalité : 21= 15 x 1 +6.
Celle de R2 de l'égalité : 15= 6 x 2 +3.
Quelle est la dernière égalité utile dans cette démarche ?

2. Faire, de même, le pavage d'un rectangle de dimensions 21 et 10 cm.
3. On se propose de payer à présent un rectangle de dimensions 210 millimètres et 188 millimètres.
La construction géométrique paraissant difficile, on va opérer algébriquement.

a. Ecrire les égalités numériques correspondant aux constructions à réaliser ; en  déduire la taille maximale des carrés qui pavent ce rectangle.