Bonsoir

La solution la plus simple est donnée par {a,b,c}={-1;0;1}



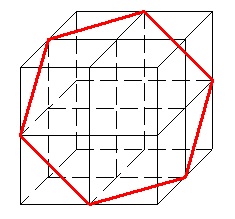
Après il est clair que si on multiplie toutes les coordonnées par un même nombre ou si on ajoute un même nombre à chaque coordonnées on conserve l'hexagone .
y-en a-t-il d'autres ?

Imod

Avec ces remarques, on peut avancer :
Commencer par supposer a < b < c .
Retrancher b donne un triplet qui vérifie a < 0 < c .
Puis diviser par a donne du 1 < 0 < c .

A partir de là, trouver c = 1 ne doit pas être très compliqué.

Oups :
Puis diviser par -a donne du -1 < 0 < c .

Bonjour,

la permutation (a,b,c) (a,c,b ) est une symétrie par rapport au plan y = z
la permutation (a, c, b) (c, a, b) une symétrie par rapport au plan x = y
la permutation (a,b,c) (c,a,b) est donc une rotation de 120° autour de l'axe x=y=z, composition dans l'espace de ces deux symétries planes
on a donc deux triangles équilatéraux dans deux plans à priori parallèles entre eux et orthogonaux à x=y=z
pour que cela forme un hexagone régulier il faut et il suffit alors que A (a, b, c) B (a, c, b) soit une rotation de même axe de 60°

vu autrement que si G ((a+b+c)/3, (a+b+c)/3, (a+b+c)/3) est l'isobarycentre des 6 points, que (GA, GB) = 60°
je laisse terminer le calcul ...

m'enfin.. bof... la remarque de verdurin dans l'autre fil montre instantanément que les six points sont dans le même plan x+y+z = a+b+c !
je n'ai fait en fait qu'ajouter les angles de 120° quels que soient a,b,c
et donc que dans ce plan les 6 points forment toujours un hexagone "presque régulier"



et qu'il suffit donc de calculer un seul angle pour qu'il le soit.

PS
ou d'ailleurs deux cotés consécutifs ... !

Je ne suis pas sur la même piste . Il me semble qu'il n'y a qu'un quadrillage 3D qui accepte l'hexagone que j'ai dessiné hier .  A partir de là , on devrait pouvoir retrouver toutes les formes {a,b,c} qui conviennent . Je mets bien sûr un paquet de conditionnels

Imod

"il me semble" n'est pas une démonstration

avec ma méthode il suffit de prouver au final que AB = BC ce qui conduit, car les points sont bien entendu différents donc a, b, c sont tous différents, à a+b = 2c
condition nécessaire et suffisante, à permutation près

Comment savoir comment les points se suivent sur le cercle de centre G et de rayon GA ?

nota : le quadrillage unique avec un hexagone est si on suppose que a, b, c sont entiers sur la base d'un certain quadrillage.
ici a,b,c sont des réels donc à priori pas forcément des points entiers d'un quadrillage 3D.

je n'ai jamais parlé d'un tel cercle ... mais oui, les points sont tous les 6 équidistant de leur isobarycentre.

on sait que les points A (a, b, c), B (a, c, b) et C (c, a, b) sont quels que soient a, b, c

- d'une part C est l'image de A par rotation de 120° autour de l'axe (en 3D !!) x=y=z
donc les trois points A (a,b,c), C (c,a,b) et E (b, c, a) forment un triangle équilatéral (dans le plan x+y+z = a+b+c)

et de même B (a, c, b), D (b, a, c), F(c, b, a) forment un autre triangle équilatéral dans le même plan

- d'autre part A et B symétriques par rapport au plan y = z (donc par rapport à une droite dans le plan x+y+z = a+b+c)

AB = BC si et seulement si B est entre A et C conduisant à l'hexagone régulier :



ou si ABC est lui-même équilatéral conduisant à des points confondus, ce qui est exclus.

Bonjour,
Un lien qui confirme ce que dit mathafou :

D'un autre côté ce que j'avais raconté n'est pas complètement idiot . En partant d'un hexagone régulier dans l'espace on peut construire de façon unique le cube précédent ( il suffit de tracer les plans perpendiculaires au plan de l'hexagone passant par les côtés ) . Dans le repère générer par le cube les coordonnées de l'hexagone sont des permutations de {-1 : 0 : 1 } . Si les coordonnées du polygone sont des permutations de {a,b,c} alors en translatant le polygone par le vecteur de coordonnées  -(a+b+c)/3  on obtient un nouveau polygone régulier avec les mêmes propriétés et a+b+c=0 .  En réduisant les dimensions du polygone on doit retomber sur le résultat .

Imod

Un peu basique :
Avec a < b < c et A(a,b,c), B(a,c,b), C(b,a,c), D(b,c,a), E(c,a,b), F(c,b,a).
Pour savoir quels sont les côtés d'extrémité A dans l'hexagone régulier, on cherche les plus petites longueurs parmi AB, AC, AD, AE et AF.

AB² = 2(c-b)²
AC² = 2(b-a)²
AD² = (b-a)² + (c-b)² + (c-a)² > 2(c-b)² car c-a > c-b.
Et AD² > 2(b-a)² car c-a > b-a.
De même AE² = (c-a)² + (b-a)² + (c-b)² > 2(c-b)²
Et AE² > 2(b-a)²
De même AF² = 2(c-a)² > 2(c-b)²
Et AF² > 2(b-a)²

Les côtés d'extrémités A sont AB et AC.
Donc 2(c-b)² = 2(b-a)².
D'où a+c = 2b.

Il n'y a pas grand-chose à retenir de mon dernier message mais on peut tout de même faire du géométriquement très simple à partir de l'exemple {-1  ; 0 ; +1)  . En effet clairement on garde un polygone régulier en effectuant sur ce polygone une homothétie de centre O suivie d'une translation quelconque . A l'opposé tout hexagone régulier dont les coordonnées sont des permutations de {a,b,c} se ramène à ce modèle de base en défaisant ces transformations . Prenons un hexagone régulier construit avec des permutations de {a,b,c} . Comme déjà dit on peut supposer que a < b < c et par une translation de vecteur (-b,-b,-b) se ramener à a < 0 < b . On note qu'alors les 6 points sont également répartis sur les axes de coordonnées , O est donc le centre de l'hexagone . Les sommets sont alors sur un cercle de centre O et b = - a . Avec une homothétie de rapport 1/b on retrouve le modèle . Ensuite il est facile de voir que ces manipulations ne sont possibles que si le b initial est au milieu de [ac] .

Imod

Un autre basique un peu calculatoire.
Toujours avec a < b < c et A(a,b,c), B(a,c,b), C(b,a,c), D(b,c,a), E(c,a,b), F(c,b,a).

Si l'hexagone ABCDEF est régulier alors le vecteur AB est égal à un des vecteurs CD, CE, CF, DE, DF, EF ou un de leurs opposés.
Seuls les vecteurs CD et EF ont une première coordonnée nulle.
AB DC car c-b > 0 et a-c < 0.
AB différent de CD car c-b c-a.
AB FE car c-b > 0 et a-b < 0.
Donc AB = EF.
Ce qui donne b = (a+c)/2.