Bonjour (et bonnes vacances pour ceux qui en profite !)

Alors voilà, j'ai un exercice à faire sur les homothéties, mais certaines choses me posent problème. C'est l'exercice 39 p368 de Maths Repères 1ère S :

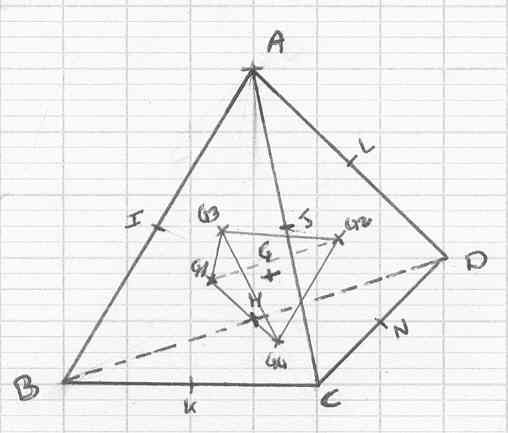
On considère un tétraèdre ABCD. On appelle G l'isobarycentre de ses sommets et G1, G2, G3, G4 les centres de gravité des triangles (ABC), (ACD), (ABD) et (BCD). (c'est la figure ci-jointe, sans les traits de construction !)

1) Montrer que GA= -3GG4 (GA, GG4 sont des vecteurs).
Alors là, c'est en fait mon plus gros problème parce que je pense que la réponse est sous mes yeux, mais je n'arrive pas à mettre le doigt dessus !

2) Quelle est alors l'image du tétraèdre ABCD par l'homothétie de centre G et de rapport -1/3 ?
Ici, comme je n'ai pas répondu à la question précèdente, je me suis dit :
GA'= (-1/3)GA= G4
GB'= (-1/3)GB= G2
GC'= (-1/3)GC= G3 (mon dessin n'est pas juste ici)
GD'= (-1/3)GD= G1

Et j'ai construit la figure.

3) Quel est le rapport des volumes de ces deux tétraèdres ?
Comme une homothétie multiplie les volumes par lkl³, alors on a :
V_G4G2G3G1= V_ABCD/3.
Ainsi, le volume du tétraèdre ABCD est trois fois plus grand que celui du tétraèdre G4G2G3G1.

Que pensez-vous de tout cela ? Pouvez-vous m'aider pour résoudre mes questions ?
Merci d'avance !