Inscription / Connexion Nouveau Sujet
probabilité
on lance un dé équilibré a dix faces (numérotées de 1 à 10)
si on obtient un multiple de 3 . alors on gagne 3 euros sinon on perd 2 euros
on relance le dé une deuxieme puis une troisieme fois
1) déterminer la liste des gains et des pertes posibles pour ce jeu puis calcule la probabilité associée a chaque gain et a chaque perte
2) En utilisant éventuellement les réponse précédente déterminer si on a intérêt à jouer .

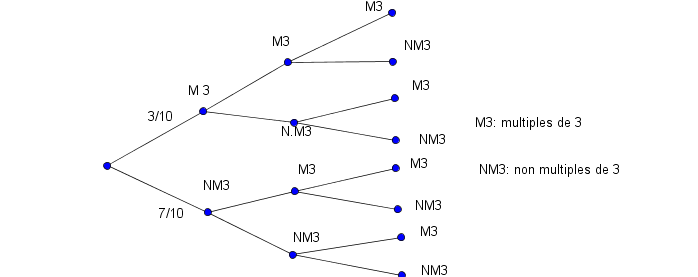
tu peux peut-être t'organiser avec un arbre
une branche pour les multiples de 3
une autre pour les non multiples de 3
...
bonjour,
les multiples de 3 sont: 3 , 6, 9
tu peux modéliser avec un arbre.
on lance le dé une fois:
Proba (multiple de 3): 3/10=
Pourquoi?
*
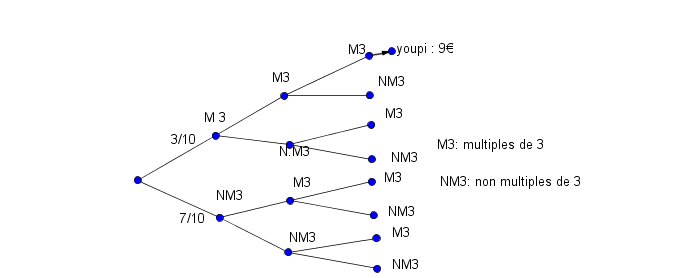
tu as vu , j'ai écrit "youpi: 9 €"
M3->M3->M3 -> 9€
Continue
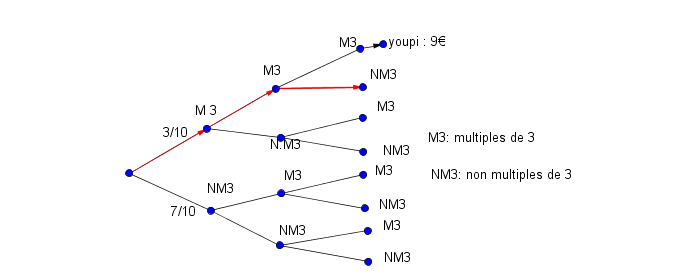
M3-> M3-->NM3-> .....€
(suis les flèches rouges)
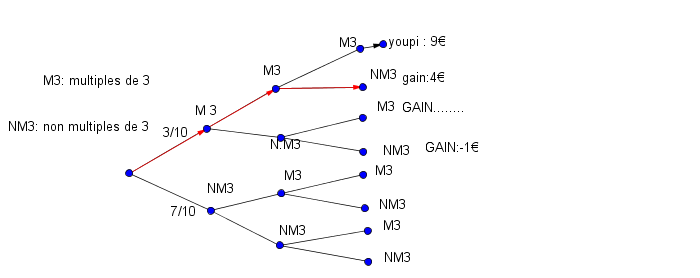
si on obtient un multiple de 3 . alors on gagne 3 euros sinon on perd 2 euros
donc 3+3-2=4
salut
en complement de l'arbre fournit par kenavo que je salue, on peut aussi faire appel à la loi binomiale de parametre B(3; 3/10) car on effectue 3 lancés indépendants ( qui sont equivalents à un tirage avec remise de boules dans une urne) .
si on prend pour variable aleatoire X = au gain correspondant au nombre de fois ou l'on obtient un multiple de 3 alors X peut prendre les valeurs -2,3,6 ,9
P(X=-2)=P(aucun multiple de 3)= C(3,0)*(3/10)^0*(1-3/10)^3
P(X=+3)=P(1 seul multiple de 3)= C(3,1)*(3/10)^1*(1-3/10)^2
P(X=+6)=P2 multiples de 3)= C(3,2)*(3/10)^2*(1-3/10)
P(X=+9)=P(3 multiples de 3)= C(3,3)*(3/10)^3*
l'esperance du gain serait ensuite E(X)=-2P(X=-2) +....+9.P(X=9)
taytay est en 3e...et ne va pas comprendre la loi binomiale....
mais bon, ce sera pour quelqu'un d'autre....