Inscription / Connexion Nouveau Sujet
problème de maths
Bonjour,
je suis en 3ème et j'ai un exercice de maths à faire seulement je n'y arrive pas. Je vous demande de l'aide car j'y ai réfléchi pas mal de temps sans parvenir à le faire.
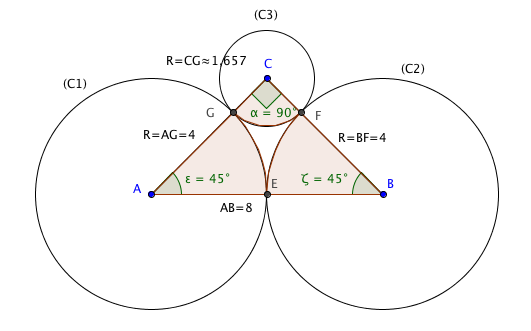
Sur la figure ci-dessus (qui n'est pas en vraie grandeur), le triangle ABC est rectangle en C.
Les points A, B et C sont les centres respectifs des cercles C1, C2 et C3.
Le rayon des cercles C1 et C2 est égal à 4cm.
Les points A, E et B sont alignés. E est le seul point d'intersection entre les cercles C1 et C2 (de même pour les points F et G).
Déterminer la valeur exacte de l'aire de la partie grisée puis son arrondi au mm² près
J'ai d'abord pensé utilisé pythagore mais je n'ai pas réussi .
Ensuite je me suis dit qu'il faudrait calculer les différentes aires des cercles mais je ne vois pas où çela peut me mener
Je suis perdu et surtout déséspéré.
Merci de votre aide prochaine
Je te conseille de calculer l'aire du triangle ABC et d'en déduire l'aire totale des trois secteurs circulaires de la figure.
Bonjour à vous deux
stabiloman
Un petit coup de pouce supplémentaire
Le triangle rectangle ABC rectangle en C est la moitié d'un carré de côté AC=BC et dont la diagonale est AB=8 cm
pour calculer l'aire de ce triangle qui est A=AC*BC/2 =AC2/2, il te faut calculer AC
aide : dans un carré de côté a, la diagonale vaut a
2 ici 8 cm
tu as donc AC2=8 et le côté AC vaut 8/2 cm
l'aire du triangle curviligne EFG= aire de ABC- aire des secteurs de cercle AGE+BEF+CGF
ces secteurs de cercle dont tu connais le rayon 4 cm et CG=AC-4 ( à na pas mettre sous forme décimale mais a garder avec 2) ont une aire proportionnelle à l'angle au centre
aire du secteur AGE=aire du secteur BEF = aire du cercle de rayon 4 cm/8 car 360°/45°=8
et l'aire du secteur CGF= aire du cercle (C3)/4 car 360°/90°=4
Annuler
connectez vous