Inscription / Connexion Nouveau Sujet
Problème en math
bonsouar tout le monde j'espère que vous allez bien..
enfaite j'ai un petit problème :$ donc le voila.. Merci de bien vouloir m'aider s'il vous plait:
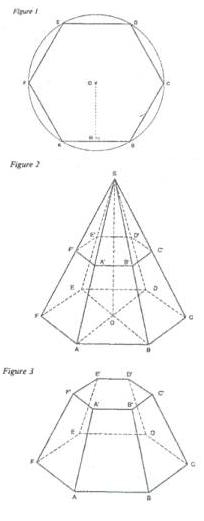
La figure 1 représente un hexagone régulier inscrit dans un cercle de centre 0 et de rayon 4cm.
(OH) est perpendiculaire à (AB)
La figure 2 représente une pyramide régulière P de sommet S et de base hexagone régulier de la figure 1.
On a coupé cette pyramide par un plan parallèle à la base.
On obtient ainsi une seconde pyramide réguière P1 de sommet S et de base hexagone régulier A'B'C'D'E'F' de côté A'B'=2.8cm.
On donne de plus AA'=BB'=CC'=DD'=EE'=FF'=6cm.
La figure 3 représente le tronc d'une pyramide extrait de la figure 2. Ce tronc représente un fromage de chèvre vendu dans le commerce.
I. On s'intéresse à la figure1
1.a) Montre que le triangle AOB est équilatéral.
b) Calcule la valeur exacte de OH.
2. Montre que la valeur exacte de l'hexagone ABCDEF est 24
3cm².
II. On s'intéresse à la figure 2
1. En utilisant le triangle SAB, démontre que SA=20cm.
2.En utilisant le triangle SOA rectangle en O, calcule la valeur exacte de SO.
3.A l'aide des résultats précédents, démontre que le volume V de la pyramide P est égal à 1922cmcube
4.La pyramide P1 est un réduction de la pyramide P.
Calcule le volume V1 de cette pyramide.
III.Calcule à partir des résultats précédents, la valeur approchée, à 1cm² près par défaut, du volume de ce fromage de chèvre
Pour le calcul de OH il faut utiliser le Théorème de Pythagore.
OH2+(AB2)/2=OA2
donc OH2=OA2-(AB2)/2
OH=42-22=12
Ce qui donne OH= 23.
Pour l'aire totale de l'hexagone il faut calculer l'air d'un triangle équilatérale.
Aire d'un triangle= (AB*OH)/2= 43
L'aire de l'hexagoen fait 6 fois l'aire d'un triangle donc l'aire de l'hexagone ABCDEF vaut 6*43=243
Bonjour,
moi, je ne vois pas comment trouver que SA=20 cm mais cette valeur connue, tu appliques Pythagore ds tr SOA rect en O et tu as :
SA²=SO²+OA²--> comme SO=20 et OA=4, tu vas trouver : SO=V(384)[V=racine carrée]
et comme 384=64*6 alors SO=8V6.
Vol gde pyr P= (1/3)*aire base*hauteur=(1/3)*(24V3)*(8V6)
............=8*(V3)*8*(V6)=64*(V18)=192*V2
On passe de la gde pyr à la petite pyr par un coeff de réduc de :
2.8/4=0.7
Donc le volume est réduit de 0.7 au cube =0.7^3=0.343 (et non pas réduit de 0.7!!).
Vol P1=192V2*0.343=65.856V2
Tu soustrais P1 de P pour trouver volume du fromage et en arrondi, tu trouves :
178 cm cube (sauf erreurs de calcul).
Salut.
Salut.
bonsouar excusez moi de vous déranger j'aimerai savoir quel est l'aire de l'hexagon s'il vous plait..
merci d'avance
*** message déplacé ***
Bonsoir pitite_moi,
Un hexagone régulier peut se décomposer en 6 triangles équilatéraux de même dimensions donc il te suffit de calculer l'aire d'un de ces triangle équilatéral pour en déduire l'aire d'un hexagone régulier.
Après la formule dépend un peu de ce que tu connais comme longueur.
Salut 
*** message déplacé ***
*6
mais de rien océane puis faut dire que c'est plus pratique pour retrouver les réponses 
merciiii de vos réponses merciiiiii biizouuuuuuuuuuuus puis bonne soirée!! ^^
bonjour j'espère que vous allez bien j'aimerai des vérifications a propos de cette exercice pouvez vous le véréfier s'il vous plait
Exercice 1 :
I.
1.a) Je sais que : O est le centre du cercle dans lequel est inscrit l'hexagone régulier ABCDEF de rayon 4cm. Et que (OH) est perpendiculaire à (AB).
Propriété : l'image du point A par la rotation de centre O est B tel que AO égale OB.
Est je sais que AO = OB = 4cm Donc le triangle AOB est un triangle isocèle en O et l'angle O fait 60° car la somme d'un cercle est de 360° et comme il y a 6 petits triangle dans cet hexagone régulier alors 360/ 6 = 60 °
Tout triangle isocèle avec un angle de 60° est équilatéral donc le triangle AOB est bien un triangle équilatéral.
Conclusion : AO est égale à OB qui sont égaux à AB car c'est un hexagone régulier donc ABO est un triangle équilatéral.
b) Dans le triangle AOH je sais que OH est la perpendiculaire à A, si le triangle AOH est rectangle alors AO sera l'hypoténuse alors d'après le théorème de Pythagore
AO² = OH² + HA² HA= AB/2 = 4/2 = 2
Donc OH² = AO² - HA²
OH² = 4² - 2²
OH= \/¯12
OH = \/¯3*4
OH = 2\/¯3
OH = 2\/¯3
2. Je calcule l'aire de l'hexagone régulier ABCDEF tel qu'il fasse 24\/¯3cm²
aire de l'hexagone régulier est x*(Bh)/2
x est égal au nombre de triangle rectangle dans l'hexagone régulier ABCDEF, qui contient 12 triangle rectangle en O
soit l'aire = 12 * (HA* OH)/2
= 12 * (2 * 2\/¯3)/2
= 12 * (4\/¯3)/2
= 12 * (2\/¯3)
= 24\/¯3cm ²
Donc l'aire de l'hexagone régulier ABCDEF est bien égal à 24\/¯3cm ²
II.
1. Je sais que cette pyramide est coupé par un plan qui est parallèle à la base donc on a une deuxième pyramide régulière de sommet S et de base hexagone régulier A'B'C'D'E'F'.
Donc SA parallèle à SB à SC à SD à SE à SF et alors SA' est aussi parallèle à SB' à SC' à SD' à SE' à SF'.
Alors d'après le théorème de Thalès :
SA'/SA = SB'/SB=AB'/AB
On pose x = SA' soit SA = x + 6
X / (x +6) = 2.8 /4 = 0.7
x = (x+6) *0.7
X = 4.2 + 0.7x
0.3x = 4.2
x = 4.2 /0.3
x = 14 = SA'
Et comme SA = SA' + 6 alors SA = 14 +6
SA = 20
2. Dans le triangle rectangle SOA qui est rectangle en O alors SA est l'hypoténuse alors d'après le théorème de Pythagore :
SA'² = SO² + AO²
Alors SO² = SA² - AO²
SO² = 20² - 4²
SO² = 400 - 16
SO = \/¯384
SO = \/¯16*24
SO = \/¯16*\/¯24
SO = 4\/¯6*4
SO = 8\/¯6.
3. Je démontre que le volume V de la pyramide P est égal à 192\/¯2cm cube.
V = 1/3* Bh*8\/¯6
V = 1/3 * 24 * 8 \/¯3*2
V= 1/3 * 192 \/¯3*\/¯2
V = 1/3 * 576 \/¯2
V= 192\/¯2cm cube.
Donc le volume de la pyramide P est bien égal à 192\/¯2cm cube.
4. Le volume V1 de la pyramide P1 est de :
V1 = Volume de la pyramide P * 14/20
V1 = 192\/¯2 * 14/20
V1 = 384 * 0.7
V1 = 268.8cm cube
le volume de la pyramide P1 est égal à 268.8cm cube.
III. Le volume de ce fromage de chèvre est de :
V= 192\/¯2 - (192\/¯2)/27
V = 261cm cube.
Bonjouuuur, j'espère que vous allez bien!
j'ai un dm de math et j'aimerai savoir si mon exercice et bon (comme on m'a pas répondu dans l'autre je le refait...
)
Merci de bien vouloir m'aider, bonne journée à vous
La figure 1 représente un hexagone régulier inscrit dans un cercle de centre 0 et de rayon 4cm.
(OH) est perpendiculaire à (AB)
La figure 2 représente une pyramide régulière P de sommet S et de base hexagone régulier de la figure 1.
On a coupé cette pyramide par un plan parallèle à la base.
On obtient ainsi une seconde pyramide réguière P1 de sommet S et de base hexagone régulier A'B'C'D'E'F' de côté A'B'=2.8cm.
On donne de plus AA'=BB'=CC'=DD'=EE'=FF'=6cm.
La figure 3 représente le tronc d'une pyramide extrait de la figure 2. Ce tronc représente un fromage de chèvre vendu dans le commerce.
I. On s'intéresse à la figure1
1.a) Montre que le triangle AOB est équilatéral.
b) Calcule la valeur exacte de OH.
2. Montre que la valeur exacte de l'hexagone ABCDEF est 243cm².
II. On s'intéresse à la figure 2
1. En utilisant le triangle SAB, démontre que SA=20cm.
2.En utilisant le triangle SOA rectangle en O, calcule la valeur exacte de SO.
3.A l'aide des résultats précédents, démontre que le volume V de la pyramide P est égal à 1922cmcube
4.La pyramide P1 est un réduction de la pyramide P.
Calcule le volume V1 de cette pyramide.
III.Calcule à partir des résultats précédents, la valeur approchée, à 1cm² près par défaut, du volume de ce fromage de chèvre
Réponnnnnnnnnse
Exercice 1 :
I.
1.a) Je sais que : O est le centre du cercle dans lequel est inscrit l'hexagone régulier ABCDEF de rayon 4cm. Et que (OH) est perpendiculaire à (AB).
Propriété : l'image du point A par la rotation de centre O est B tel que AO égale OB.
Est je sais que AO = OB = 4cm Donc le triangle AOB est un triangle isocèle en O et l'angle O fait 60° car la somme d'un cercle est de 360° et comme il y a 6 petits triangle dans cet hexagone régulier alors 360/ 6 = 60 °
Tout triangle isocèle avec un angle de 60° est équilatéral donc le triangle AOB est bien un triangle équilatéral.
Conclusion : AO est égale à OB qui sont égaux à AB car c'est un hexagone régulier donc ABO est un triangle équilatéral.
b) Dans le triangle AOH je sais que OH est la perpendiculaire à A, si le triangle AOH est rectangle alors AO sera l'hypoténuse alors d'après le théorème de Pythagore
AO² = OH² + HA² HA= AB/2 = 4/2 = 2
Donc OH² = AO² - HA²
OH² = 4² - 2²
OH= \/¯12
OH = \/¯3*4
OH = 2\/¯3
OH = 2\/¯3
2. Je calcule l'aire de l'hexagone régulier ABCDEF tel qu'il fasse 24\/¯3cm²
aire de l'hexagone régulier est x*(Bh)/2
x est égal au nombre de triangle rectangle dans l'hexagone régulier ABCDEF, qui contient 12 triangle rectangle en O
soit l'aire = 12 * (HA* OH)/2
= 12 * (2 * 2\/¯3)/2
= 12 * (4\/¯3)/2
= 12 * (2\/¯3)
= 24\/¯3cm ²
Donc l'aire de l'hexagone régulier ABCDEF est bien égal à 24\/¯3cm ²
II.
1. Je sais que cette pyramide est coupé par un plan qui est parallèle à la base donc on a une deuxième pyramide régulière de sommet S et de base hexagone régulier A'B'C'D'E'F'.
Donc SA parallèle à SB à SC à SD à SE à SF et alors SA' est aussi parallèle à SB' à SC' à SD' à SE' à SF'.
Alors d'après le théorème de Thalès :
SA'/SA = SB'/SB=AB'/AB
On pose x = SA' soit SA = x + 6
X / (x +6) = 2.8 /4 = 0.7
x = (x+6) *0.7
X = 4.2 + 0.7x
0.3x = 4.2
x = 4.2 /0.3
x = 14 = SA'
Et comme SA = SA' + 6 alors SA = 14 +6
SA = 20
2. Dans le triangle rectangle SOA qui est rectangle en O alors SA est l'hypoténuse alors d'après le théorème de Pythagore :
SA'² = SO² + AO²
Alors SO² = SA² - AO²
SO² = 20² - 4²
SO² = 400 - 16
SO = \/¯384
SO = \/¯16*24
SO = \/¯16*\/¯24
SO = 4\/¯6*4
SO = 8\/¯6.
3. Je démontre que le volume V de la pyramide P est égal à 192\/¯2cm cube.
V = 1/3* Bh*8\/¯6
V = 1/3 * 24 * 8 \/¯3*2
V= 1/3 * 192 \/¯3*\/¯2
V = 1/3 * 576 \/¯2
V= 192\/¯2cm cube.
Donc le volume de la pyramide P est bien égal à 192\/¯2cm cube.
4. Le volume V1 de la pyramide P1 est de :
V1 = Volume de la pyramide P * 14/20
V1 = 192\/¯2 * 14/20
V1 = 384 * 0.7
V1 = 268.8cm cube
le volume de la pyramide P1 est égal à 268.8cm cube.
III. Le volume de ce fromage de chèvre est de :
V= 192\/¯2 - (192\/¯2)/27
V = 261cm cube.
*** message déplacé ***
si j'oublie de mettre les figures ça le fait moyen excusez moi lol
** image supprimée **
*** message déplacé ***
salut
le 1 c'est tout bon
pour le 2 y'a une ptite erreur qd tu écris
Donc SA parallèle à SB à SC à SD à SE à SF et alors SA' est aussi parallèle à SB' à SC' à SD' à SE' à SF'. c'est surement pas bon car toutes ces droites se coupent en S donc elles sont pas //
ce que tu veux dire je pense c'est (A'B') // (AB) car on coupe la pyramide avec un plan // à la base
et donc effectivement tu appliques thalés comme tu l'as fait
les résultats semblent correctes
pour le reste ça a l'air bon (sauf étourderies de ma part) sauf que j'aimerais bien comprendre comment tu trouves ça
V1 = Volume de la pyramide P * 14/20
le 14/20 il vient d'où?
si tu arrives à expliquer ça
c'est tout bon
bye
*** message déplacé ***
la FAQ du forumbonjour
à la question 4 calcul de V1 n'est pas egal à 384 car
ce qui pourrait donner 271.529 * .7 = 190.07
*** message déplacé ***
Merci océane mais je le connais c'est juste qu'on me répondait pas et moi j'ai pas toute ma vie pour savoir si c'est juste ou pas donc maintenant je me retrouver a 1h du matin en train de recopier mon devoir maison de math en étant a peu prêt sur de mes réponses c'est pour ça excusez moi mais bon demain j'ai cours a 8h avec deux heures de physiques donc euh c'est un peu short donc merci de un peu raissonnable cela dit c'est la première fois que je le fait donc voila!
Merci de votre éventuel compréhension bonsoir euuh bonne nuit
Annuler
connectez vous