Inscription / Connexion Nouveau Sujet
Problème produits scalaire
Bonjour à tous, j'ai un problème à faire mais je j'arrive pas :s Est ce que je pourrai avoir de l'aide s'il vous plait merci d'avance.
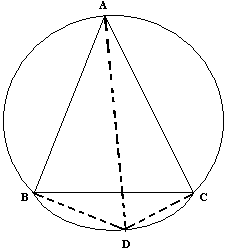
On considère un triangle équilatéral ABC et son cercle circonscrit ainsi qu'un point D appartenant au petit arc-de-cercle BC. Le but du problème est de prouver que, quelle que soit la position de D sur l'arc BC, on a toujours AD=BD+CD. ( construction de la figure: reponter au compas les longueurs BD et CD sur le segement AD, puis en recommencant en changeant plusieurs fois la position du point D)
1. Justifiez que l'on a Angle BDA= angle CDA= /3
/3
2. A l'aide de l'égalité d'al kashi, exprimez AB2en fonction de BD et AD, puis AC2 en fonction de DC et AD.
3. Déduisez en que (BD-DC)(BD+DC-AD)=0
4.concluez ( distinguez les cas BD-DC=0 et BD-DC 0)
0)
Bonsoir
On te dit que D a une position quelconque sur l'arc BC
Choisir comme sur la figure annexée D diamétralement opposé à A est juste de nature à partir sur des constations fausses.
Il me semble qu'en seconde, tu ne peux pas totalement ignorer que deux angles inscrits dans un cercle et interceptant le même arc sont égaux et que par conséquent l'angle ADB=angle ACB= /3
/3
appliquer la formule d'al Kashi dans 2 triangles ne nécessite pas de connaissance autre que celle d'ouvrir ton cours à la page où est donnée la formule.
et dans les 2 cas l'angle opposé à AB d'une part et à AC d'autre part étant égaux et AB=AC,
l'égalité est facile à écrire et la démonstration qui suit est vraiment fort simple
AB²=DB²+AD²-2AD.DBcos /3
/3
AC²=DC²+AD²-2AD.DCcos /3
/3
comme AB²=AC²
AB²-AC²=0=DB²-DC²+2ADcos /3(DC-DB)
/3(DC-DB)
=(DB-DC)(DB+DC-2ADcos /3)
/3)
et comme cos /3=1/2
/3=1/2
2ADcos 3=AD
3=AD
donc
(DB-DC)(DB+DC-AD)=0
si DB DC
DC
on a bien
AD=DB+DC
si DB=DC
AD=2DB
dans ce cas le point D est diamétralement opposé à A
AD est le diamètre du cercle
Cela signifie que BC=BD=R du cercle



