Inscription / Connexion Nouveau Sujet
problème trigonométrie
Bonjour , je ne sait pas comment faire cet exercice pouvez vous m'aider s'il vous plait ? merci d'avance .
le problème et tel :
Clément veut déterminer la hauteur EC d'un arbre situé de l'autre coté d'une rivière .
pour cela il mesure avec un théodolite il recule ensuite de 30 m , et mesure à nouveau l'angle obtenu .
il est alors satisfait et en déduit la hauteur de l'arbre .
Déterminer la hauteur EC de l'arbre au mètre près .
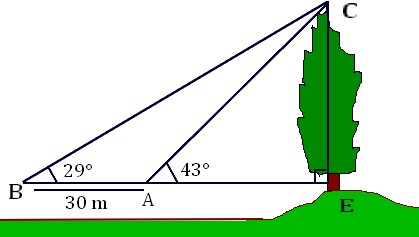
re bonjour,
avec la trigo, tu peux écrire une égalité où figurera EC
tan43=EC/AE
tan29=EC/BE= EC/(30+AE)
EC = tan43 * AE = tan29 * (30 + AE)
détermine d'abord AE, ensuite EC
n'hésite pas à poser tes qst
par la trigonométrie
ici grace au tangente des angles (tan d'un angle = cote opp / coté adjacent)
résoud la petite équation que je t'ai proposé, tu vas voir
Mais je voit pas comment étant donné que ns avons pour seule mesure BA et que pour déterminer AE il faudrait BC non ?
pourquoi ne fais tu pas l'équation que j'ai t'ai mise dans mon 1er post à 11h16
certes, cette exo n'est pas des plus faciles mais je t'ai donné la marche à suivre
si tu n'arrives pas à résoudre l'équation pour trouver d'abord AE
dis moi, on voit ca ensemble
ok, je te montre
tan 43° * AE = tan 29° *(30+AE)
tan43 * AE = 30 * tan 29 + tan29 * AE (tu développes ici)
tan43 * AE - tan29 * AE = 30 * tan 29 (ici tu isoles AE, ton inconnue)
AE (tan43 - tan 29 ) = 30 * tan 29 (tu factorises)
AE = (30 * tan 29) / (tan43 - tan 29)
a ta calculatrice
que trouves tu ?
as tu compris la résolution maintenant ?
je te laisse faire la suite
(Désolé pour hier ordinateur HS)
pour 62 j'ai calculer
AE = (30 * tan 29) / (tan43 - tan 29) donc j'ai hésiter entre simplifier les 29 mais au final j'ai multiplié la première ligne
30 * 29 = 870
et soustrait le dénominateur
43-29= 14
870/14=62 m


