Bonjour

C'est mieux de ne pas écrire en Majuscules car ton message est à moitié illisible et fait mâl à nos gentils yeux

Ensuite :

0<x<10 car si  X > 10 alors le dieuxième est nécéssairement : X < 10 or  x = x (hum...) Donc x < 10
Je pense que c'est à poursuivre dans cette voie !

Bonjour,
une remarque : il est très impoli d'écrire en majuscules, cela équivaut à "hurler dans les oreilles" des personnes qui t'écoutent, tu ne ferais jamais cela je suppose..... n'est-ce pas ?.....

je voulais m'excuser pour avoir écrit en majuscules, je ne voulais pas hurler dans les oreilles. Merci de m'avoir prévenu
pour de ce qui est le problème je n'ai rien fait, j'essaye je suis allé retourné dans mon livre et dans mon cours mais je ne comprends rien du tout si vous pouviez m'avancer cela m'aiderait peut-etre merci;

excuses acceptées ....

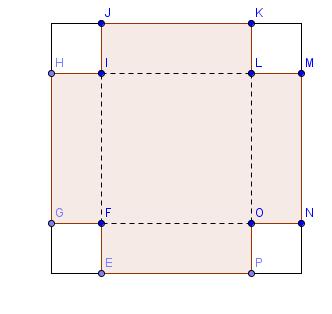
je joins un petit schéma, tu dois en avoir un sous les yeux...

pour la 1ère question : la réponse me semble évidente puisque la feuille dans laquelle on découpe la boîte est un carré de 10 cm de côté....

pour la 2nde : la hauteur de la boîte correspond, sur mon dessin, au segment [IJ] ou [KL]..
combien mesurent ces segments ?

pour la 3ème : combien mesure [IL] ? 10 - ......

pour la 4ème : volume de la boîte = Aire de la baseIJ

voila déjà pour démarrer...

merci pour vos excuses. Mais là je suis perdu car je n'ai aucune mesure à part les 20 cm de côté de la boite donc la hauteur je la remplace par x et je travaille avec les 20 cm

..pour la question 1 je voulais écrire...

sur le dessin que j'ai joint, x correspond à la mesure des segments [IJ], [HJ]...
as-tu compris pourquoi il faut que 0 < x < 10 ?

non je n'ai pas compris, je suis nul en géométrie et je crois que je fais des calculs inutils alors je me perds et je crois que c'est plus simple

dans la plaque de carton on enlève aux quatre coins un petit carré de côté x cm,
la longueur restante est JK (sur le dessin) et tu peux écrire
JK = 20 - 2x : pour qu'il reste du carton il est indispensable que la quantité enlevée soit inférieure à 20 cm c'est à dire 2x < 20 ou x < 10.

ensuite, comme on enlève un peu de carton cela signifie que x > 0
d'où 0 < x < 10

as-tu compris ?...

Tilk tu as écrit :


pour la 1ère question : la réponse me semble évidente puisque la feuille dans laquelle on découpe la boîte est un carré de 10 cm de côté....

Or dans l'éconcé :

Une boite est frabiqué dans une plaque de carton carré de 20 cm de coté. Pour cela on coupe des carrés de x cm et on plie le long des pointillés !
As-tu mal lu ? Ou est-ce moi que qui ne comprend pas (perso je crois en la dieuxième solution )

Donc je mentiens mon idée :

0<x<10 car si  X > 10 alors le dieuxième est nécéssairement : X < 10 or  x = x (hum...) Donc x < 10

Quelqu'un peut m'expliquer comment "Citer" car je n'ai pas compris et ca m'aiderai bien

Bonjour,

On peut retourner la question en : si x=12 (par exemple), comment fais-tu ton découpage ?



    RAPPEL : IJ=FE=x et le côté du grand carré fait 20cm...

je crois que j'ai compris si JK= 20-2x alors x=20/2=10 donc x=10 est-ce cela

Il faudrait plutôt rédiger avec des inéquations, mais l'idée est là.

JK + 2x = 20
2x = 20 - JK

or JK est compris entre 0 et 20, donc :

20 - 20 < 2x < 20-0
0 < 2x < 20
0 < x < 10

Merci pour le conseil Porcepic

donc x est compris entre 0 et 10 car il faut que la quantité enlevée soir inférieur à 20 cm. Pour la hauteur l'aire et le volume vous pourriez m'aider merci

Bonjour ala0,
bonjour Porcepic,

oui, j'avais fait une erreur, le côté de la plaque en carton mesure 20 cm et non 10 cm....(j'étais à côté de la plaque si j'ose dire...)

il est donc évident qu'on ne peut pas enlever plus de la moitié de la longueur...

quelle est la hauteur de la boîte ?...ou combien mesure IJ ?

quelle est la largeur de la boîte ? ou combien mesure IL ?

De rien tilk

Pour la 2) oui c'est combien mesure IJ
Donc on a le choix entre : la hauteur mesure 1IJ .....mais bon
Ou alors: X- .... je sais pas
Ou encore : donnée non fourni par l'énoncé qui nous est proposé (un peu pompeux mais bon on fera avec )

Marioulle il n'y a rien d'autre dans ton énoncé ??

on n'a pas besoin d'autres dimensions, le volume de la boîte est fonction de x...
la hauteur de la boîte est x
la largeur de la boîte est (20 - 2x)
et donc le volume de la boîte est....

bonjour
on suppose que la boîte n'a pas de dessus
pour rendre les choses plus claires, autour du périmètre du grand carré, on peut écrire x près des côtés des petits carrés
il apparaît que x > 0 et que 2x < 20 donc que 0 < x < 10
quand on relèvera les bords, la boîte aura une hauteur de x et une base carrée de côté IL = 20-2x

ce que je remarque c'est que tous les résultats obtenus sont de 10

tout compte fait je n'ai encore rien compris à cette exercie la hauteur à part IJ la largeur IL mais pour l'aire et le volume je suis dans le noir c'est imcompréhensible

pour moi la hauteur = 20-2x donc x=10
pour l'aire =c²= 100 cm²
et je coince pour le volume quelqu'un peut-il m'aider merci

après le volume de la boite, il me demande de compléter un tableau de valeurs avec x =0,1,2,3,4,5,6,7,8,9 et 10 calculer la valeur de A(x) et V(x) donc je prends comme équation 20-2x et je remplace x par les nombres au dessus merci de répondre:?

bonjour
tu peux essayer de dessiner et de découper un patron, puis d'en relever les bords pour former la boîte et d'en constater quels en sont la hauteur et le côté de la base
le volume d'un parallélépipède est l'aire de sa base fois sa hauteur
l'aire d'une base carrée est le carré de son côté
ici le côté de la base est 20-2x
l'aire de la base est (20-2x)²
la hauteur est x
le volume est (20-2x)² * x

serait-il possible que la hauteur fasse 10 cm car 20-2x=x=20/2donc x=10 si c'est cela on peut facilement connaitre l'aire et le volume croyez vous que j'ai bon merci

si quelqu'un pouvait m'aider sur cet exercice ce serait sympa j'y  suis depuis ce matin c'est un casse tête t je ne trouve pas merci

pour l'aire j'ai repris l'équation de plumemeteore c'est à dire (20-2x)²je l'ai converti et j'ai trouvé x=324 est-ce cela pour le volume comme on ne connait pas la hauteur j'ai fait v=324xX est-ce cela

pour la hauteur j'ai fait 20-2x=10
pour l'aire j'ai fait (20-2x)²=324
pour le volume = (20-2x)²x X = 324X

je me suis trompé pour le volume jai fait v=324x10=3240
ca doit pas etre ca corrigez moi SVP merci
:?

Bonsoir,
la hauteur est x et ne peut donc être égale à 10 puisque x < 10...

la largeur est (20 - 2x) : ce que tu as fait est incorrect.

L'aire du carré de base est (20 - 2x)² et donc le volume est
V(x)=x(20 - 2x)² et c'est terminé pour le volume.

pour la question suivante, il faudrait que tu nous donnes le tableau de valeurs dont on parles dans l'énoncé ...
il faut calculer le volume pour ces valeurs de x...

Par exemple pour x = 1
tu remplaces x par 1 dans la formule donnant le volume et tu effectues les calculs
V(1) = 1(20-21)²=(20 - 2)² = 18²= 324
pour x = 2

V(2) = 2(20-22)²=2(20 - 4)² = 216²=2256=512

pour x = 3
V(3) =3(20-23)²=3(20 - 6)² = 314²=3196=588

et ainsi de suite...
quand tu auras rempli le tableau de valeurs tu pourras répondre à la question suivante...

merci pour tes explications
pour le tableau de valeurs il me demande aussi l'aire à remplir comme A(x) = (20-2x)² je remplace mon x par le nombre donné exemple A(2)= (20-2x)²=(20-2*2)²=(20-4)²=16²=256 est-ce cela si c'est bon je vous remercie tous

Bonjour,
oui, ton calcul est bon...

bonjour,
je dois montrer que l'aire en cm² du carré du fond de la boîte est donné par la fonction:
A(x) = (20-2x)²
puis développer et réduire A(x)